注：本文节选自《50 Years of CFD in Engineering Sciences》，Runchal, A. (Ed.). (2020).

”

1 介绍

1.1 背景

2012年，Runchal[1]谈到了CFD的发展方向及未来的CFD，其中预测随着CFD技术的发展，CFD将被嵌入到特定的应用程序中，并与 EVR（工程虚拟现实）软件及设计工具相集成。然而至今为止，这一天似乎还未到来。事实上，甚至可以说近些年CFD 的发展在一定程度上停滞不前，或者至少与十年前的情况相比，没有显示出任何重大的革命性地变化。但可以肯定的是，近年来CFD在许多方面仍然取得了一些进步：计算机系统功能更强、软件更人性化、行业应用大幅增长。根据IMARC Group[2]的研究，2018 年全球CFD市场价值约 16 亿美元，预计 2024 年将增长至约 31 亿美元，复合年增长率 (CAGR) 约为 11 %。然而CFD在过去十年的基本局限性今天依然困扰着我们。事实上，讨论计算流体动力学前景的早期年度回顾[3]提到了类似的局限性。CFD的主要缺点之一是，对于许多实际应用计算时间过长。然而当前所使用的求解算法仍然是上世纪八十年代和九十年代初使用的算法的变体，尽管它们有一些改进。

然而，我们认为近年来出现了一个根本的变革驱动力-机器学习。这项技术已经在改变我们的生活，我们相信机器学习将对我们生活中的几乎每个方面产生实质性的影响，当然也包括CFD。这里我们将探讨这些发展对CFD和计算科学的潜在影响。

1. Runchal, A. K. (2012). The future ofCFD and the CFD of the future. Computational Thermal Sciences: An International Journal, 4(6), 517–524.
2. IMARC Group (2019). Computational Fluid Dynamics Market: Global Industry Trends, Share, Size, Growth, Opportunity and Forecast 2019–2024. https://www.imarcgroup.com/computational-fluid-dynamics-market (last accessed 22 June 2019) Patterson, G. S., Jr. (1978). Prospects for computational fluid mechanics. Annual Review of Fluid Mechanics, 10(1), 289–300.

1.2 当前CFD的局限

在文献[1]中提到的CFD局限性在今天仍然存在，其中包括以下方面：

1. 网格生成

• 费时且难以自动化
• 难以生产高质量的网格
• 复杂几何体产生的非最优网格和非必要的大量网格

2. CFD易用性
• 复杂的初始条件与边界条件
• 难以适应不同的物理场景
3. 计算速度
• 大多数程序需要求解大型矩阵方程
• 高度并行和网格计算系统的低效代码
4. 稳健性
• 你能让你的模拟无人看管吗？
• 大型矩阵和迭代求解器
• 受到截断误差和不收敛的影响
5. 物理知识的缺乏
• 湍流
• 化学
• 纳米级物理学
• 非线性、非平衡等
• 热辐射
• 多相流
6. 随机过程的不确定性
• 不确定性的本质是什么？
• 如何考虑不确定性？
7. 对预测结果的信心
• 验证和确认
• 设计输入注意事项

2 CFD的未来：人工智能和机器学习的影响

2.1 人工智能/机器学习技术的复兴

在过去的几年里，人们对统计机器学习及其相关应用产生了浓厚的兴趣。特别是人工神经网络尤其是在深度神经网络和机器视觉领域[4,5]自2012年以来迎来了回潮。我们大多数人都亲身体验过人工智能和大数据对我们日常生活的深刻影响：自动驾驶汽车、自然语言界面、语音识别、手写识别、人类语言之间的机器翻译、医学成像，这还只是少数几个例子。因此研究人工智能对CFD和计算模拟技术的影响是合乎逻辑的。下面我们将简要描述人工智能（如物理信息深度神经网络[6,8])对CFD产生深刻影响的方式，然后我们将尝试预见未来几年的发展方向。

人工神经网络 (ANN) 似乎是目前最强大的机器学习技术。图 1 显示了一个人工神经网络的示意图。典型的前馈人工神经网络由一个输入层、一个或多个隐藏层及一个输出层组成。每一层从前一层获取输入，使用一组权重执行线性变换，然后通过激活函数执行非线性变换，并将其输出传递到下一层。此过程如式(1)所示。

其中 是合适的非线性函数，如 sigmoid、tanh、relu等。具有足够多隐藏层的人工神经网络是泛函逼近器。具有大量隐藏层的人工神经网络通常被称为深度神经网络。

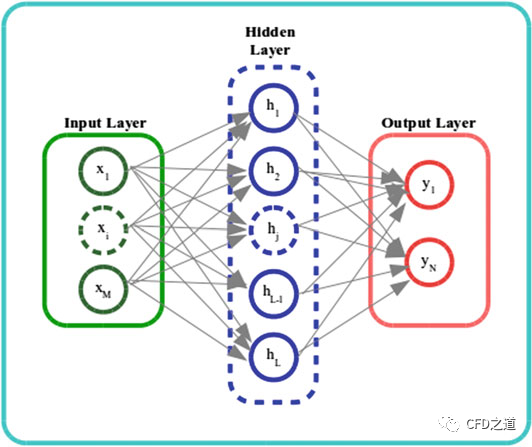
图 2 是一个基于物理信息的神经网络示意图 [6]。这是最近的一项创新，其将 Navier-Stokes 方程与其他守恒定律的残差纳入到训练网络时使用的目标函数/损失函数中，这些残差包括：

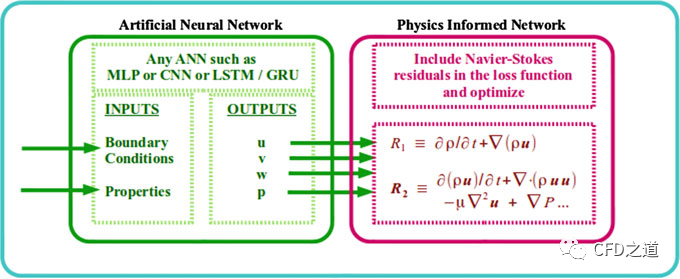
空间梯度与时间梯度通常通过自动微分来计算。一些用于机器学习的开源库（如 TensorFlow、Pytorch等）能够提供这种自动微分的功能[7]。这种方法已经被证明对于由微分方程控制的系统具有更好的精度[8]，因此是一种非常有前途的方法。最近的另一项创新是使用数据驱动的神经网络而非常用的有限差分法对偏微分方程进行离散[9]。

4. Krizhevsky, A., Sutskever, I., & Hinton, G. E. (2012). Imagenet classification with deep convolutional neural networks. In Advances in Neural Information Processing Systems (pp. 1097–1105).
5. Goodfellow, I., Bengio, Y., & Courville, A. (2016). Deep learning. MIT Press.
6. Raissi, M., Perdikaris, P., and Karniadakis, G. E. (2017). Physics informed deep learning (part i): Data-driven solutions ofnonlinear partial differential equations. arXiv:1711.10561.
7. Abadi, M., Agarwal, A., Barham, P., Brevdo, E., Chen, Z., Citro, C., & Ghemawat, S. (2016). Tensorflow: Large-scale machine learning on heterogeneous distributed systems. arXiv:1603.04467.
8. Kani, J. N., & Elsheikh, A. H. (2017). DR-RNN: A deep residual recurrent neural network for model reduction. arXiv:1709.00939
9. Bar-Sinai, Y., Hoyer, S., Hickey, J., & Brenner, M. P. (2019). Learning data-driven discretizations for partial differential equations. arXiv:1808.04930

2.2 降阶模型

计算机的处理能力在过去的几十年里有了长足的进步。然而即使在当前的硬件基础上，CFD计算也需要大量的内存和CPU资源。当需要为诸如控制、反问题、最优设计等实时上下文[10]进行重复求解时，对计算资源的需求将变得更加具有挑战性，因此需要开发适当的降阶模型来减少存储和CPU需求。常用的模型降阶技术包括本征正交分解(Proper Orthogonal Decomposition，POD)[11-14]和/或动态模式分解(Dynamic Mode Decomposition，DMD)[15-19]。文献[20]几何POD与深度神经网络开发了一个代理模型，用于计算患者特定模型的主动脉应力分布，其利用POD来表征主动脉的几何形状，并根据结构有限元预测的应力来训练深度神经网络。

10. Lassila, T., Manzoni, A., Quarteroni, A., & Rozza, G. (2014). Model order reduction in fluid dynamics: Challenges and perspectives. In Reduced Order Methods for Modeling and Computational Reduction (pp. 235–273). Springer.
11. Narasimha, R. (2011). Kosambi and proper orthogonal decomposition. Resonance, 16(6),574–581.
12. Berkooz, G., Holmes, P., & Lumley, J. L. (1993). The proper orthogonal decomposition in the analysis of turbulent flows. Annual Review ofFluid Mechanics, 25(1), 539–575.
13. Bui-Thanh, T., Damodaran, M., and Willcox, K. (2003). Proper orthogonal decomposition extensions for parametric applications in compressible aerodynamics. In 21st AIAA Applied Aerodynamics Conference (p. 4213).
14. Bui-Thanh, T., Damodaran, M., & Willcox, K. E. (2004). Aerodynamic data reconstruction and inverse design using proper orthogonal decomposition. AIAA journal, 42(8), 1505–1516.
15. Schmid, P. J. (2010). Dynamic mode decomposition of numerical and experimental data.Journal of Fluid Mechanics, 656, 5–28.
16. Tu, J. H., Rowley, C. W., Luchtenburg, D. M., Brunton, S. L., & Kutz, J. N. (2013). On dynamic mode decomposition: Theory and applications. arXiv:1312.0041.
17. Kutz, J. N., Brunton, S. L., Brunton, B. W., & Proctor, J. L. (2016). Dynamic mode decomposition: data-driven modeling of complex systems. SIAM.
18. Proctor, J. L., Brunton, S. L.,&Kutz, J. N. (2016).Dynamicmode decomposition with control. SIAM Journal on Applied Dynamical Systems, 15(1), 142–161.
19. Williams, M. O., Kevrekidis, I. G., & Rowley, C. W. (2015). A data–driven approximation of the koopman operator: Extending dynamic mode decomposition. Journal of Nonlinear Science, 25(6), 1307–1346.
20. Liang, L., Liu, M., Martin, C., & Sun, W. (2018). A deep learning approach to estimate stress distribution: a fast and accurate surrogate of finite-element analysis. Journal of the Royal Society, Interface, 15(138), 20170844.

2.3 数字孪生技术

数字孪生是物理产品、过程或服务的虚拟复制品[21]。Digital Twins结合了多种物理模拟、数据分析、机器学习和物联网，以确保在产品或过程的生命周期内准确建模。数字孪生被Gartner评为2019年十大战略技术趋势之一[22]。根据文献 [23]的观点，模型降阶是数字孪生技术的核心组成部分，因为其允许实时仿真和模型交换，大大降低了知识产权风险。

21. Grieves, M., & Vickers, J. (2017). Digital twin: Mitigating unpredictable, undesirable emergent behavior in complex systems. In Transdisciplinary Perspectives on Complex Systems (pp. 85–113). Springer.
22. Kerremans, M., Burke, B., Cearley, D., & Velosa, A. (2019). Top10 strategic technology trends for 2019: Digital Twins. Gartner Research, Document ID:G00377678. https://www.gartner.com/en/documents/3904569/top-10-strategic-technology-trends-for-2019-digital-twin. Retrieved 11 July 2019.
23. Hartmann, D., Herz, M., & Wever, U. (2018). Model order reduction a key technology for digital twins. In Reduced-Order Modeling (ROM) for Simulation and Optimization (pp. 167-179). Springer.

2.4 湍流模拟

湍流建模是深度学习应用的一个肥沃领域。Duraisamy及其同事[24-29]开发了一个名为场反演与机器学习(Field Inversion and Machine Learning，FIML)的框架。他们的策略是在标准RANS模型（如Spalart-Allmaras）的产生项中引入一个DataInformed修改器，用于改进特定问题类别（如翼型计算）中的预测。网络的训练数据来自实验测量和/或高保真计算（DNS或LES）结果。要注意的是，产生项修正器在性质上是乘法的，并且是一个场变量。产生项修正/校正是通过求解一个反问题来得到的，该反问题使RANS结果与高保真/实验数据之间的差异最小。在文献 [26]中训练了一个神经网络来输出给定一些流动特征作为输入的校正。输入的流动特征包括逆压梯度指示器、产耗比、应变率（幅度）与涡度（幅度）之比等。在文献[28]中考虑了其他流动特征，如平均速度梯度和湍流时间尺度作为模型的输入。

与Duraisamy的方法相反，Ling及其同事使用深度神经网络，在他们对RANS模型的数据信息修正中，专注于保持伽利略不变性[30,32]。特别是，它们保持旋转不变性。在神经网络中至少有三种保持不变性的方法。一种是通过增量地旋转/平移坐标系，通过旋转/平移给定数据来生成附加训练数据。另一种方法是利用等变滤波器将等变构建到卷积神经网络[31]中。第三种方法是确保模型的输入本身是不变的。文献[30]使用由应变率张量和旋转率张量形成的10个各向同性基张量来确定标量系数，然后用这些标量系数来计算雷诺应力各向异性张量。进一步利用雷诺应力各向异性张量增强了二次涡粘模型的预测能力。深度神经网络的输入总是来自RANS模型的结果，然而训练数据是基于高保真的LES或DNS计算的结果。他们总共使用了六个规范流动进行训练，一个用于优化神经网络超参数，两个用于测试。与标准的二次涡粘模型相比，他们获得了更高的精度。其他研究人员如xiao及其同事也遵循了类似的方法，他们在参考文献[33]和[34]中引入了压力梯度、湍动能梯度和壁距，从而增强了输入特性。

Weatheritt[37]和相关的工作[35，36]采取了一些不同的方法，这些工作侧重于代数雷诺应力模型。这些研究还根据张量基和标量不变量提出了各向异性张量的分解。然而通过符号回归和基因表达式编程(GEP)得到了表达式的代数形式。训练数据的作用是评估候选表达式并找到最佳匹配。特别是在参考文献[35]中，他们还将CFD计算集成到评估步骤中，因为在高保真（LES或DNS）数据上训练的雷诺应力表达式可能产生不一致甚至病态的RANS模型。他们已经对Newrans模型与涡轮尾流混合计算进行了测试，在预测精度上有了显著提高。文献[36]还比较了GEP+符号回归的结果与深度神经网络在横流射流背景下的性能，并在线性涡粘模型的基线模拟上改进了结果。

深度学习在湍流建模中的其他应用包括在流入边界为LES/DNS生成合成湍流（随时间变化）[38]、亚网格尺度建模[39]、湍流燃烧建模，特别是亚网格尺度反应速率[40，41]以及通过学习潜在吸引子生成湍流[42]。

24. uraisamy, K., Iaccarino, G., & Xiao, H. (2019). Turbulence modeling in the age of data. Annual Review ofFluid Mechanics, 51, 357–377.Duraisamy, K., & Durbin, P. (2014). Transition modeling using data driven approaches. In CTR Summer Program (p. 427).
25. Holland, J. R., Baeder, J. D., & Duraisamy, K. (2019). Towards integrated field inversion and machine learning with embedded neural networks for RANS modeling. In AIAA Scitech 2019 Forum (p. 1884).
26. Singh, A. P., Medida, S., & Duraisamy, K. (2017). Machine-learning-augmented predictive modeling of turbulent separated flows over airfoils. AIAA Journal, 2215–2227.
27. Singh, A. P., & Duraisamy, K. (2016). Using field inversion to quantify functional errors in turbulence closures. Physics ofFluids, 28(4), 045110.
28. Parish, E. J., & Duraisamy, K. (2016). A paradigm for data-driven predictive modeling using field inversion and machine learning. Journal ofComputational Physics, 305, 758–774.
29. Ling, J., Kurzawski, A., & Templeton, J. (2016). Reynolds averaged turbulence modeling using deep neural networks with embedded invariance. Journal of Fluid Mechanics, 807,155–166.
30. Thomas, N., Smidt, T., Kearnes, S., Yang, L., Li, L., Kohlhoff, K., & Riley, P. (2018). Tensor field networks: Rotation-and translation-equivariant neural networks for 3d point clouds.arXiv:1802.08219
31. Ling, J., Jones, R., & Templeton, J. (2016). Machine learning strategies for systems with invariance properties. Journal ofComputational Physics, 318, 22–35.
32. Wu, J. L., Xiao, H., & Paterson, E. (2018). Physics-informed machine learning approach for augmenting turbulence models: A comprehensive framework. Physical Review Fluids, 3(7).
33. Wang, J. X.,Wu, J. L., & Xiao, H. (2017). A Physics-informed machine learning approach for reconstructing Reynolds stress modeling discrepancies based on DNS data. Physical Review Fluids, 2(3).
34. Zhao,Y., Akolekar, H. D.,Weatheritt, J., Michelassi,V., &Sandberg, R. D. (2019). Turbulence model development using CFD-driven machine learning. arXiv:1902.09075
35. Weatheritt, J., Sandberg, R. D., Ling, J., Saez, G., & Bodart, J. (2017). A comparative study of contrasting machine learning frameworks applied to RANS modeling of jets in crossflow. GT2017-63403. In Proceedings of the ASME Turbo Expo 2017: Turbomachinery Technical Conference and Exposition, GT2017, June 26–30, 2017, Charlotte, USA.
36. Weatheritt, J. (2015). The development of data driven approaches to further turbulence closures (Doctoral dissertation, University of Southampton).
37. Fukami, K., Kawai, K., & Fukagata, K. (2018). A synthetic turbulent inflow generator using machine learning. arXiv:1806.08903
38. Maulik, R., San, O., Jacob, J. D., & Crick, C. (2019). Sub-grid scale model classification and blending through deep learning. Journal ofFluid Mechanics, 870, 784–812.
39. Lapeyre, C. J., Misdariis, A., Cazard, N., Veynante, D., & Poinsot, T. (2019). Training convolutional neural networks to estimate turbulent sub-grid scale reaction rates. Combustion and Flame, 203, 255–264.
40. Nikolaou, Z. M., Chrysostomou, C., Vervisch, L., & Cant, S. (2018). Modelling turbulent premixed flames using convolutional neural networks: application to sub-grid scale variance and filtered reaction rate. arXiv:1810.07944
41. Mohan, A., Daniel, D., Chertkov, M., and Livescu, D. (2019). Compressed convolutional LSTM: An Efficient deep learning framework to model high fidelity 3D turbulence. arXiv:1903.00033

2.5 多相流

人工神经网络在多相流的模拟中得到了广泛的应用。在文献 [47]中，作者训练了一个神经网络用来计算两种不混溶流体（通常是气-液）之间的由VOF计算的界面曲率，通常曲率通过计算法线到界面的梯度来计算的。这个法线本身是用平滑的体积分数场的梯度计算出来的。通过训练ANANNANTO估计曲率，可以显著降低此操作的费用。文献 [48]中将一种基于物理信息的深层递归神经网络与基于Pod-Galerkin投影的ROM相结合，对油藏中的两相油水流动进行了模拟。深度神经网络已经被训练用来预测两相泡状流中的气泡尺寸[49]。在文献 [50]中使用CFD模拟的数据训练鼓泡塔反应器的深度神经网络模型。文献[51]中构建了一种沸腾传热的神经网络模型。

47. Qi, Y., Lu, J., Scardovelli, R., Zaleski, S., & Tryggvason, G. (2019). Computing curvature for volume of fluid methods using machine learning. Journal ofComputational Physics, 377,155–161.
48. Kani, J. N.,&Elsheikh, A. H. (2019).Reduced-order modeling ofsubsurface multi-phase flow models using deep residual recurrent neural networks. Transport in Porous Media, 126(3),713–741.
49. Montes-Atenas, G., Seguel, F., Valencia, A., Bhatti, S. M., Khan, M. S., Soto, I., et al. (2016).Predicting bubble size and bubble rate data in water and in froth flotation-like slurry from computational fluid dynamics (CFD) by applying deep neural networks (DNN). International Communications in Heat and Mass Transfer, 76, 197–201.
50. Mosavi, A., Shamshirband, S., Salwana, E., Chau, K. W., & Tah, J. H. (2019). Prediction of multi-inputs bubble column reactor using a novel hybrid model of computational fluid dynamics andmachine learning. EngineeringApplications ofComputational FluidMechanics, 13(1),482–492.
51. Liu, Y., Dinh, N., Sato, Y., & Niceno, B. (2018). Data-driven modeling for boiling heat transfer: Using deep neural networks and high-fidelity simulation results. Applied Thermal Engineering, 144, 305–320.

2.6 CFD压缩

深度神经网络已经被用于压缩CFD模拟结果。文献[43]采用了一种特别创新的方法来压缩高阶间断Galerkin计算的结果。基于神经网络的自动编码器与本征正交分解相结合，以形成计算结果的紧凑表示。采用径向基函数的向量核正交贪婪算法来学习动力学。之后可以根据需要随时从压缩状态恢复CFD结果。文献[44]使用基于神经网络的自动编码器来形成格子玻尔兹曼模拟的压缩表示。

43. Carlberg, K. T., Jameson, A., Kochenderfer, M. J., Morton, J., Peng, L., & Witherden, F. D. (2018). Recovering missing CFD data for high-order discretizations using deep neural networks and dynamics learning. arXiv:1812.01177.
44. Hennigh, O. (2017). Lat-net: Compressing lattice Boltzmann flow simulations using deep neural networks. arXiv:1705.09036

2.7 收敛加速及数值稳定性

可以使用深度神经网络加速离散系统和/或线性离散系统的求解。文献[45]使用卷积神经网络来加速压力泊松方程的求解，该方程用于加强不可压缩流动中的散度约束。在文献[46]中，神经网络通过调节人工粘性来控制不连续点附近的数值振荡。通常CFD求解器有许多可调节的参数，如松弛参数、内迭代等，这些参数用于保证迭代格式的收敛性，深度神经网络可以用来学习这些参数的最优值，以获得最快的收敛性，同时保持稳定性。

45. Tompson, J., Schlachter, K., Sprechmann, P., & Perlin, K. (2017). Accelerating Eulerian fluid simulation with convolutional networks. In Proceedings ofthe 34th International Conference on Machine Learning (Vol. 70, pp. 3424–3433).
46. Discacciati, N., Hesthaven, J. S., & Ray, D. (2019). Controlling oscillations in high-order Discontinuous Galerkin schemes using artificial viscosity tuned by neural networks. https://infoscience.epfl.ch/record/263616/files/Artificial_viscosity_nn.pdf. Retrieved 23 June 2019.

2.8 几何，网格生成，可视化和后处理

深度神经网络(DNN)已经被用于几何分类，尤其是在医学成像等领域。设计了卷积神经网络来帮助处理二维或三维结构化数据的图像。然而最近深度神经网络被扩展到学习非结构化数据和/或原始点云[54,55]。DNN也被用于CAD模型的处理和修复[56]。它们也被期望在PLM中扮演越来越重要的角色[57]。虽然DNN在网格划分中的应用还相对较少[58]，但它已经被用于CFD和FEM模拟结果的可视化和后处理。一个典型的应用是在3D和4D(3d空间+时间）中识别旋涡[59，60]。在未来的几年里，这一应用程序将继续受到更多的关注和发展。

54. Wu, Z., Song, S., Khosla, A., Yu, F., Zhang, L., Tang, X., & Xiao, J. (2015). 3d shapenets: A deep representation for volumetric shapes. InProceedings ofthe IEEEconference on computer vision and pattern recognition (pp. 1912–1920).
55. Qi, C. R., Su, H., Mo, K., & Guibas, L. J. (2017). Pointnet: Deep learning on point sets for 3d classification and segmentation. In Proceedings ofthe IEEE Conference on Computer Vision and Pattern Recognition (pp. 652–660).
56. Danglade, F., Pernot, J. P., & Véron, P. (2014). On the use of machine learning to defeature CAD models for simulation. Computer-Aided Design and Applications, 11(3), 358–368.
57. Dekhtiar, J., Durupt, A., Bricogne, M., Eynard, B., Rowson, H., & Kiritsis, D. (2018). Deep learning for big data applications in CAD and PLM–Research review, opportunities and case study. Computers in Industry, 100, 227–243.
58. Yao, S., Yan, B., Chen, B., & Zeng, Y. (2005). An ANN-based element extraction method for automatic mesh generation. Expert Systems with Applications, 29(1), 193–206.
59. Deng, L., Wang, Y., Liu, Y., Wang, F., Li, S., & Liu, J. (2019). A CNN-based vortex identification method. Journal ofVisualization, 22(1), 65–78.
60. Rajendran, V., Kelly, K. Y., Leonardi, E., & Menzies, K. (2018). Vortex detection on unsteady CFD simulations using recurrent neural networks. AIAA 2018–3724.

2.9 不确定性量化

在数值模拟中有几个不确定性来源。这些不确定性包括几何（包括由于制造公差引起的不确定性）、物理、材料属性、初始条件、边界条件等方面。例如，尽管饱和地下水流量可以以确定性的方式计算[61，62]，但介质本身受到很大的变异性的影响。土壤的导水率、补给率等需要考虑为随机变量[63]。文献[64]提出了不确定性量化(UQ)的框架，文中综述了多项式混沌技术[65]。然而UQ在计算上相当昂贵，因为其需要多次（数百甚至数千次）评估模型[66]。参考文献[67][68]中考虑了 UQ 的扩展以利用物理信息神经网络，这似乎是一种有前途的方法。。

61. Analytic and Computational Research, Inc. (2019) The PORFLOW® Reference Manual.https://www.acricfd.com/
62. Harbaugh,A.W.,Banta,E.R., Hill,M.C.,&McDonald,M.G. (2000).MODFLOW-2000,The U.S. geological survey modular ground-water model-user guide to modularization concepts and the ground-water flow process. Open-file Report. U. S. Geological Survey, 92, 134
63. Hill,M. C.,&Tiedeman, C. R. (2006). Effective groundwatermodel calibration:With analysis ofdata, sensitivities, predictions, and uncertainty. ISBN 9780471776369, Wiley.
64. Roy, C., & Oberkampf, W. (2010). A complete framework for verification, validation, and uncertainty quantification in scientific computing. In 48th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, AIAA (pp. 2010–124).
65. Najm, H. N. (2009). Uncertainty quantification and polynomial chaos techniques in computational fluid dynamics. Annual Review ofFluid Mechanics, 41, 35–52.
66. Tripathy, R. K., & Bilionis, I. (2018). Deep UQ: Learning deep neural network surrogate models for high dimensional uncertainty quantification. Journal of Computational Physics, 375, 565–588.
67. Yang, Y., & Perdikaris, P. (2018). Adversarial uncertainty quantification in physics-informed neural networks. arXiv:1811.04026
68. Zhu, Y., Zabaras, N., Koutsourelakis, P. S., & Perdikaris, P. (2019). Physics-constrained deep learning for high-dimensional surrogate modeling and uncertainty quantificationwithout labeled data. Journal ofComputational Physics, 394, 56–81.

（完）