本文描述代数方程组求解中的两种基础迭代法：雅可比迭代法与高斯-赛德尔迭代法。

1 雅克比迭代法

代数方程组可以写成矩阵形式：

若系数矩阵的对角线元素不为0，则第一个方程可以用来求解，第二个方程可以用来求解，以此类推。该方法的第一步是给未知向量赋猜测值。基于这些猜测值计算新的近似值，首先是，然后，直到，这个过程表示一个迭代步。所得结果作为下一步迭代的新猜测值，并重复这个求解过程，直到两个连续迭代步之间解的变化小于一个近乎零的值，或者满足预先设定的收敛标准。此时，便得到了最终解。

在此方法中，若假定当前估计值为，则通过下式可以获得新的估计值：

式（2）表明，迭代中得到的值并不用于当前迭代步中的后续计算，而是保留到下一个迭代步才使用。利用矩阵表示方法，将式进行展开，其矩阵形式为

根据式（3）对进行求解，计算结果如下∶

系数矩阵写成下面的形式：

借助式(5)，式(4)简写为：

矩阵是一个对角矩阵，其逆矩阵非常容易获取。

只要，雅可比方法就会收敛。包括对角占优矩阵在内的一大类矩阵都满足该条件，其中在对角占优矩阵中，系数满足：

2 高斯-赛德尔迭代法

高斯-赛德尔法是比雅可比迭代法更流行的一种迭代法，它具有更好的收敛性。因为它不需要将新的估计值存储在单独的数组中，因此它不需要占用太多的内存。准确地说，该方法在计算过程中使用的最新的可用估计值。

该方法的迭代公式为：

式(7)的矩阵形式可以写为：

矩阵是一个下三角矩阵，很容易求得其逆矩阵。

实际上，高斯-赛德尔法在迭代过程中一直使用最新的值，具体而言，这些最新的值是指$j

尽管在一些情况下，雅可比方法收敛速度更快，但是高斯-赛德尔法是优先选用的方法。

3 示例

分别采用高斯-赛德尔法和雅可比方法求解下面中的方程组，分别执行5个迭代步，并计算每个迭代步的结果与精确解的误差。已知精确解为

。

解：设初始值为

。用上标标记前一个迭代步的值，则雅克比方法的求解过程如下：

误差计算公式为。则第一迭代步的计算结果为：

注：这里的误差使用真值与当前迭代值的差值。实际迭代计算时使用的是当前迭代值与上一步迭代值的差值。因为在实际应用中，真值是未知的。

”

以相同的方式继续计算，并将上一个迭代步的结果作为下一个迭代步的猜测值，如下表所示。

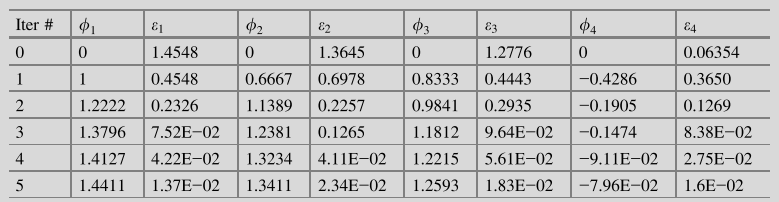
同样用上标标记前一个迭代步的值，高斯-赛德尔法的求解过程为：

第一个迭代步的计算结果：

重复相同的步骤进行计算，结果如下所示。

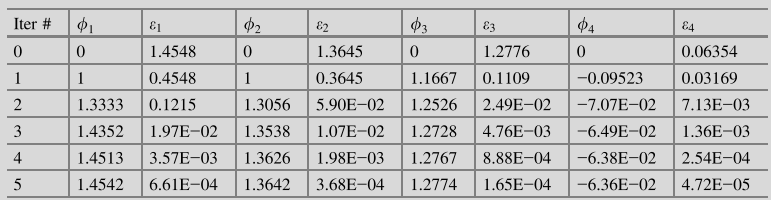
雅可比迭代法程序：

import numpy as np
# A为系数矩阵，b为结果矩阵
# k为最大迭代次数，tol为容差限
def Jacobi(A,b,k,tol):
    n = A.shape[1]
    D = np.eye(n)
    D[np.arange(n),np.arange(n)] = A[np.arange(n),np.arange(n)]
    LU = A - D
    X = np.zeros(n)
 
    # 迭代k次
    for i in range(k):
        X1= X.copy()
        D_inv = np.linalg.inv(D)
        X =  -np.dot(np.dot(D_inv,LU),X) + np.dot(D_inv,b)
 
        if(np.max(np.abs(X-X1))            print('计算收敛!')
            break
        print('n第',i,'次迭代：',X)
        print('残差值为：',np.abs(X-X1))
        print('当前最大残差为：', np.max(np.abs(X-X1)))
    return X
 
A = np.array([
    [3, -1, 0,0],
    [-2, 6, -1,0],
    [0,-2, 6,-1],
    [0, 0, -2,7]
])
b = np.array([3, 4, 5,  -3])
X = Jacobi(A, b, 1000,0.005)

输出结果为：

第 0 次迭代：[ 1.              0.66666667      0.83333333     -0.42857143]
残差值为：[1.             0.66666667     0.83333333     0.42857143]
当前最大残差为：1.0
 
第 1 次迭代：[ 1.22222222      1.13888889      0.98412698     -0.19047619]
残差值为：[0.22222222     0.47222222     0.15079365     0.23809524]
当前最大残差为：0.4722222222222222
 
第 2 次迭代：[ 1.37962963      1.23809524      1.18121693     -0.14739229]
残差值为：[0.15740741     0.09920635     0.19708995     0.0430839 ]
当前最大残差为：0.1970899470899471
 
第 3 次迭代：[ 1.41269841      1.3234127       1.22146636     -0.09108088]
残差值为：[0.03306878     0.08531746     0.04024943     0.05631141]
当前最大残差为：0.08531746031746001
 
第 4 次迭代：[ 1.44113757      1.34114386      1.25929075     -0.07958104]
残差值为：[0.02843915     0.01773117     0.03782439     0.01149984]
当前最大残差为：0.03782438901486507
 
第 5 次迭代：[ 1.44704795      1.35692765      1.26711778     -0.06877407]
残差值为：[0.00591039     0.01578378     0.00782703     0.01080697]
当前最大残差为：0.015783782648862044
 
第 6 次迭代：[ 1.45230922      1.36020228      1.2741802      -0.06653778]
残差值为：[0.00526126     0.00327463     0.00706242     0.00223629]
当前最大残差为：0.007062422264614288
计算收敛!

高斯-赛德尔迭代法程序：

import numpy as np
 
# A为系数矩阵，b为结果矩阵
# k为最大迭代次数，tol为容差限
def Jacobi(A,b,k,tol):
    n = A.shape[1]
    D = np.eye(n)
    D[np.arange(n),np.arange(n)] = A[np.arange(n),np.arange(n)]
    LU = A - D
    # 得到LU的上、下三角矩阵
    L = np.tril(LU)
    U = np.triu(LU)
    D_L = D + L
    X = np.zeros(n)
 
    # 迭代k次
    for i in range(k):
        X1= X.copy()
        D_L_inv = np.linalg.inv(D_L)
        X =  -np.dot(np.dot(D_L_inv,U),X) + np.dot(D_L_inv,b)
 
        if(np.max(np.abs(X-X1))            print('计算收敛!')
            break
        print('n第',i,'次迭代：',X)
        print('残差值为：',np.abs(X-X1))
        print('当前最大残差为：', np.max(np.abs(X-X1)))
    return X
 
A = np.array([
    [3, -1, 0,0],
    [-2, 6, -1,0],
    [0,-2, 6,-1],
    [0, 0, -2,7]
])
b = np.array([3, 4, 5,  -3])
X = Jacobi(A, b, 1000,0.001)

输出结果为：

第 0 次迭代：[ 1.              1.              1.16666667     -0.0952381 ]
残差值为：[1.             1.             1.16666667     0.0952381 ]
当前最大残差为：1.1666666666666665
 
第 1 次迭代：[ 1.33333333      1.30555556      1.2526455      -0.07067271]
残差值为：[0.33333333     0.30555556     0.08597884     0.02456538]
当前最大残差为：0.33333333333333326
 
第 2 次迭代：[ 1.43518519      1.35383598      1.27283321     -0.0649048 ]
残差值为：[0.10185185 0.04828042 0.0201877  0.00576792]
当前最大残差为：0.10185185185185186
 
第 3 次迭代：[ 1.45127866      1.36256509      1.27670423     -0.06379879]
残差值为：[0.01609347     0.00872911     0.00387102     0.00110601]
当前最大残差为：0.016093474426807752
 
第 4 次迭代：[ 1.45418836      1.36418016      1.27742692     -0.06359231]
残差值为：[0.0029097      0.00161507     0.00072269     0.00020648]
当前最大残差为：0.002909702975840478
计算收敛!

注：本文内容采集自《The Finite Volume Method in Computational Fluid Dynamics》及《计算流体力学中的有限体积法》。

”

（完）