简单案例体会SIMPLE算法

一个简单的案例描述SIMPLE算法的使用流程。

SIMPLE算法采用分离方式求解压力速度耦合方程。其基本步骤包括：

1. 假设压力场与速度场
2. 利用假设的压力场，求解动量方程计算得到速度场
3. 利用满足动量方程的速度场更新质量流量，得到
4. 利用新的质量流量求解压力修正方程，得到压力修正量
5. 更新速度场与压力场，得到新的速度场，压力场
6. 检查收敛性，若不收敛则转到第(2)步继续计算，直至计算收敛

举个简单的例子来说明此过程。如下图所示的水管系统，动量方程可写成：

其中，D为系数，, , , , ，。利用SIMPLE算法计算网络中未知的流量与压力。

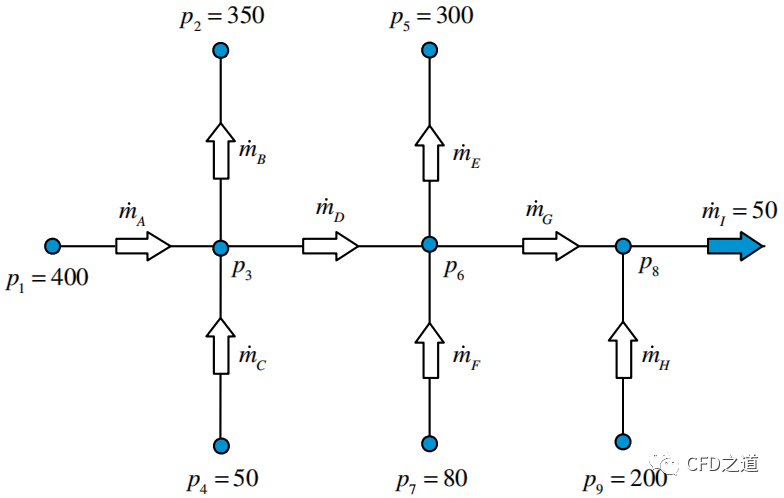
图中，需要确定的压力值包括，流量值包括。需要注意的是，流量与压力之间存在关联。

1、假设初始值

可以假设初始压力值。理论上讲，初始值可以随意假设。不过不良的初始值会导致计算收敛缓慢，甚至发散的问题。采用一个简单的原则进行压力初始值假定：压力值沿流动方向不断降低。

这里假设压力初始值为：。

由于流量与压力之间显式相关，因此无需初始流量值。

2、基于初始压力值计算流量值

代入初始压力值，可以得到流量值：

这里得到的流量值不一定满足流量守恒。

3、判断守恒

通过计算所有内部节点的流量值来检查质量流量是否满足连续性，即有：

节点3（流出为正，流入为负）：

节点6：

节点8：

因此质量不守恒。内部节点的流量应当为零。

因此需要进行修正。

4、推导压力修正方程

假设节点3、6、8的修正压力分别为，其他节点的压力值已知，无需进行修正，即修正压力为零。因此可以得到各修正流量：

根据质量守恒，对于3、6、8节点，有：

即有：

将式（7）代入式（9）可得：

代入系数值后可得到：

将（3）式的流量值代入式（11）得到方程组：

求解得到压力修正值：

得到压力修正值后，计算新的流量值：

更新3、6、8节点的压力值：

5、检测流量平衡

检查3、6、8节点的流量平衡。

因此质量平衡。

根据式（11）可得新的压力修正方程为：

求解可得到：

修正量为零，表示前面计算得到的是最终解。

6、最终结果

可得到压力值：

流量值为：

注意，流量正负表示方向。

注：本案例采集自《The Finite Volume Method in Computational Fluid Dynamics：An Advanced Introduction with OpenFOAM® and Matlab®》，为方便理解，对书中的叙述方式进行了调整。

”

SIMPLE算法理解起来比较困难，需要仔细体会。本案例仅用于帮助理解SIMPLE算法中的假设-修正过程，工程中的管路模型要比案例复杂得多，而且压力损失系数（案例中的参数D）并非常数，通常为流量的函数，求解起来要麻烦不少，不过总体思路差不太多。

（完毕）