本文描述Fluent中常用的离散方法。

注：内容取自Fluent Theory Guide 24.3。

”

主要内容包括：

• 空间离散
• 时间离散
• 梯度和导数的计算
• 梯度限制器

1 空间离散

流体输运方程可离散为下面的形式：

式中，为网格面的数量；为通过网格面的的对流值；为穿过网格面的质量通量；为面的面积向量；为面上的变量的梯度；为网格体积。

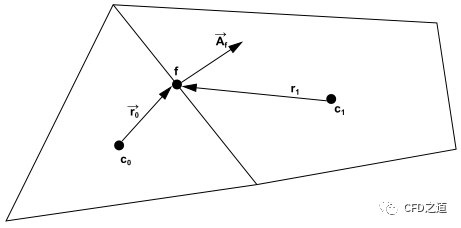
默认情况下，Fluent将标量的离散值存储在网格中心上（上图中的及）。然而通用输运方程的对流项计算需要利用到网格面上的值，因此需要利用网格中心的值进行插值计算来获取。这里常常使用迎风算法来实现。

1.1 一阶迎风格式

当需要一阶精度时，网格面上的物理量值是通过假设任何场变量的网格中心值代表一个网格内该变量的平均值。因此，当选择一阶迎风格式（First-Order Upwind Scheme）时，此时假设网格面上的物理量值直接等于其上游网格的网格中心处该物理量的值。

一阶迎风格式可以用于压力基求解器与密度基求解器。

1.2 二阶迎风格式

当需要二阶精度时，使用多维线性重构方法^[1]计算单元面上的物理量。在这种方法中，通过对以网格为中心的关于网格质心的解进行泰勒级数展开，可以在网格面获得更高的精度。因此，当选择二阶迎风(Second-Order Upwind Scheme)时，使用以下表达式计算网格面上的值φ：

式中，及分别为以网格中心的值及其上游网格中的梯度值。为从上游网格中心到面中心的位移向量。此格式需要确定每个网格中的物理量梯度 。最后梯度受到限制，不会引入新的最大值或最小值。

二阶迎风格式可以用于密度基和压力基求解器中。

1.3 一阶到高阶的混合格式

在某些流动条件下，由于局部流动波动（物理或数值）的原因，使用高阶离散格式可能无法收敛到稳态解。另一方面，对于相同的流动条件，用一阶离散格式可以得到收敛解。对于这种类型的流动和情况，如果需要比一阶更精确的解，则可以使用一阶到高阶的混合格式来获得收敛的稳态解。

仅当使用高阶离散时，一阶到高阶混合才适用。它适用于下列离散格式：二阶迎风格式、中心差分格式、QUICK格式和三阶MUSCL格式。混合不适用于一阶、修正的HRIC格式，也不适用于几何重构和CICSAM格式。

在密度基求解器中，混合作为比例因子应用于梯度重构。而在压力基求解器中，混合应用于对流输运变量的高阶项。

混合格式需要使用TUI命令打开：

/solve/set/numerics

1.4 中心差分格式

当使用尺度解析模拟(SRS)湍流模型(例如LES)时，动量方程可以使用二阶精度的中心差分离散（Central Differencing Scheme）格式。该格式提高了SRS计算的精度。

中心差分格式采用下面的方式计算网格面上的变量值：

式中，索引值与表示共享面的网格；及是网格0和1处的重构梯度；为网格中心到网格面的向量。

众所周知，中心差分格式会产生无界解和非物理振荡，这会导致数值过程的稳定性问题。如果对中心差分格式使用延迟校正，这些稳定性问题通常是可以避免的。在此方法中，面值计算如下：

UP代表迎风。如式中所示，迎风部分被隐式处理，而中心差分和迎风之间的差异进行显式处理。如果数值解收敛，这种方法将转化为纯二阶差分。

注意：中心差分格式仅在密度基求解器下可用。

1.5 有界中心差分格式

由于中心差分格式数值扩散较小，因此在尺度解析模拟（SRS）模型（如LES、DES等）中被广泛使用。然而，中心差分格式常导致求解非物理振荡。在LES中，较低的亚网格尺度湍流扩散率会加剧这种情况。

有界中心差分（Bounded Central Differencing，BCD）格式基于正则变量图（NVD）方法^[2]和对流有界性准则（ convection boundedness criterion，CBC）。有界中心差分格式是由纯中心差分格式、中心差分与迎风格式的混合格式以及一阶迎风格式所组成的复合NVD格式。在原始NVD方法中，当违反CBC时，使用一阶迎风格式，以抑制任何局部非单调性。将该方法应用于湍流尺度解析模拟的经验表明，它有时会产生过高的数值耗散。因此，在Fluent压力基求解器中实现了BCD格式的可调版本。BCD的有界强度可以通过一个参数来控制，当非单调性相对较低时，该参数允许松弛严格的CBC，并保持对局部非单调求解物理场的中心差分。

此参数可以被指定为常量或表达式，并且可以在0到1的范围内变化。最大值1对应于严格的CBC，这使得BCD方案更稳定，但耗散更大。最小值0将使BCD有界性完全失效，并使格式变为纯中心差分。对于简单流动(直槽流、自由混合层流、平板边界层流)，0.25的参数值是最优的，并被选为默认值。对于复杂的流动，可能需要更高的值来提供稳定性和分辨率之间的最佳平衡。0.75左右的水平已被发现是合适的。请注意，可调BCD格式仅在压力基求解器中可用。

BCD格式的非线性有时会导致迭代时间推进格式的收敛性降低。冻结BCD格式的中心差分和迎风分量的加权系数有助于改善这种情况下的收敛性。可以使用TUI命令激活此冻结：

solve/set/advanced/bcd-weights-freeze

该命令启动一个对话框，要求输入迭代数量，之后在每个时间步冻结BCD格式的权重。

主要：前面的描述是针对压力基求解器中的有界中心差分格式；在密度基求解器中也可以使用类似但不相同的BCD方案。在压力基求解器中，有界中心差分格式是LES、DES、SAS、SDES和SBES湍流模型的默认动量离散格式。

”

1.6 QUICK格式

对于四边形和六面体网格这类可以识别唯一上下游网格面的网格，Fluent还提供了计算面上对流变量高阶值的QUICK格式^[3]。QUICK格式基于二阶迎风加权平均及变量的中心插值。

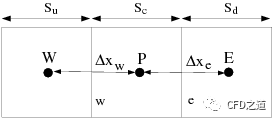
如上图所示的网格系统，若流动方向为从左至右，网格面上的变量值的计算方法可表示为：

式中，得到一个二阶中心差分；得到二阶迎风格式。传统的QUICK格式设置。Fluent中使用与计算结果相关的变量值，选择该值是为了避免引入新的计算极值。

在与流动方向一致的结构网格上，QUICK通常会更加精确。注意，Fluent 允许对非结构或混合网格使用QUICK格式。在这种情况下，非六面体（或2D中的非四边形）网格将使用二阶迎风格式。当使用并行求解器时，在分区边界上也将使用二阶迎风格式。

注意：QUICK格式在压力基求解器中可用，在密度基求解器中求解其他标量方程时也可用。

”

1.7 三阶MUSCL格式

该三阶对流格式由原始的MUSCL格式^[4]（守恒定律的单调上游中心格式）混合中心差分格式及二阶迎风格式构思而成：

式中，采用前面中心差分格式计算；通过二阶迎风格式计算。

与仅适用于结构化l六面体网格的QUICK格式不同，MUSCL格式适用于任意网格。与二阶迎风格式相比，三阶MUSCL有可能通过减少数值扩散来提高所有类型网格的空间计算精度，尤其是对于复杂的三维流动，并且该格式适用于所有输运方程。

注意：当前在Fluent中实现的三阶MUSCL格式不包含任何梯度限制器。因此当所考虑的流场具有不连续性（如激波）时，它会产生下冲和超冲。另外MUSCL格式可用于压力基与密度基求解器。

1.8 Modified  HRIC格式

对于使用VOF多相模型的模拟，迎风格式通常不适合于界面跟踪，因为它们具有过度数值扩散的性质。虽然中心差分格式通常能够保持界面的锐度，但该格式是无界的，常会给出非物理的计算结果。为了克服这些缺陷，Fluent使用了高分辨率接口捕获(High Resolution Interface Capturing，HRIC)格式的改进版本。改进的HRIC方案是由迎风和顺风差分的非线性混合组成的复合NVD格式^[5]。

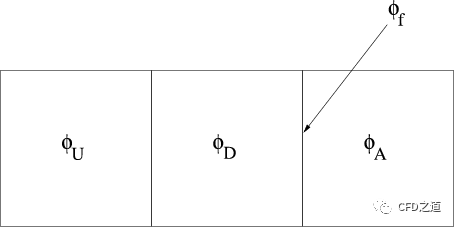
首先，对上图所示的网格方案，计算体积分数的归一化单元值，并将其用于找出归一化网格面值，如下所示：

其中A是受体网格，D是供体网格，U是迎风网格，而且有：

在这里，如果迎风网格不可用(如非结构化网格)，则使用外推值。如果流动平行于界面，则直接使用此值会导致界面出现褶皱。因此，Fluent基于面法线和界面法线之间的角度切换到最终QUICK格式：

这样可以得到面体积分数的校正版本：

式中，

其中，为网格中心到网格面的向量。

现在从上面计算的归一化值获得面体积分数，如下所示：

与QUICK格式和second-order格式相比，modified HRIC格式能够提高VOF计算的精度，并且比Geo-Reconstruct 格式的计算成本更低。

1.9 高阶项松弛

高阶格式可以写成一阶格式加上高阶格式的附加项。高阶项松弛（High Order Term Relaxation）可以应用于这些附加项。

高阶项的欠松弛遵循任何通用属性的标准公式：

其中是欠松弛系数。请注意，稳态情况下的默认值为0.25，瞬态情况下的默认值为0.75。相同的因子应用于所有求解的方程。

2 时间离散

瞬态模拟必须在空间和时间上离散控制方程。时间相关方程的空间离散化与稳态情况相同。时间离散化涉及微分方程中每一项在时间步长上的积分。瞬态项的积分很简单，如下所示。

变量的时间演化的一般表达式如下所示：

其中函数包含任何空间离散。如果使用向后差分对时间导数进行离散化，则一阶精度时间离散如下所示：

式中，为标量值；为下一个时间点，；为当前时间，。

时间导数项被离散后，仍需要进行考虑，主要是利用哪个时间进行计算。

2.1 隐式时间积分

隐式时间积分（Implicit Time Integration）。

一种计算的方法是利用下一个时间点进行计算：

这种方式称为隐式积分，因为计算过程中涉及到下一个时间点的数据。转换表达方式为：

在移动到下一个时间步之前，该隐式方程可以在每个时间级别迭代求解。

全隐式格式的优点是它对于时间步长是无条件稳定的。

2.2 有界二阶隐式时间积分

有界二阶隐式时间积分（Bounded Second-Order Implicit Time Integration）。

任何自变量都可以在时间上离散为：

式中，均为不同时间点；及为时间点及上的有界因子。

有界变量包括：

• 多相流：体积分数
• 湍流：湍动能、湍流耗散率、比耗散率
• 反应流：组分质量分数、预混/非预混变量

使用有界二阶隐式格式时存在以下限制：

• 不适用于密度基求解器，仅用压力基求解器
• 不适用于运动变形网格
• 只适用于隐式多相体积分数离散格式，不适用于显式体积分数格式
• 不支持Singhal空化模型

2.3 可变时间步长的二阶时间积分

Fluent的默认二阶时间积分格式基于可变时间步长格式。该格式引入了通用时间导数离散化，支持在任意时刻使用可变时间步长。

通用二阶离散如下所示：

式中，为时间步长比，定义为：

以及

式中，为当前时间步长；为前一个时间步长；为前前时间步长。

当使用固定时间步长时，

因此：

因此，通用方程变成如下定义的固定时间步长格式：.

对于有界二阶隐式格式，必须包括时间步长比作为作用于和的因子，每个变量在和时间级别的边界因子，因此有：

注意：用于二阶时间积分的可变时间步长格式仅适用于固定网格或滑移网格。对于动网格，使用固定时间步长格式。

2.4 显式时间积分

仅当使用密度基求解器时，显式时间积分（Explicit Time Integration）才可用，其中的值采用显式方法计算（基于因变量的现有解）：

其称为显式积分，因为的值可以用现有的解值来显式表示：

这里，时间步长被限制为求解器的稳定极限(即时间步长受Courant-Friedrichs-Lewy条件的限制)。为了准确计算时间，计算域中的所有网格必须使用相同的时间步长。为稳定起见，此时间步长必须是计算域中所有局部时间步长中的最小值。此方法也称为“全局时间步进”。

显式时间步进的使用是相当严格的，其主要用于捕捉移动波(如激波)的瞬态行为，因为在这种情况下，其比隐式时间步长方法更准确，成本更低。在以下情况下不能使用显式时间步进：

• 使用压力基求解器或密度基的隐式格式进行计算：显式时间步长公式仅适用于密度基显式格式。Fluent还将多级龙格-库塔显式时间积分用于密度基求解器。
• 不可压缩流动：不能使用显式时间推进来计算时间精确的不可压缩流动。
• FAS多重网格和残差平滑不能与显式时间推进一起使用，因为它们会破坏底层求解器的时间精度。

3 梯度及导数计算

梯度不仅用于在网格面上构造标量值，而且用于计算二次扩散项和速度导数。流动守恒方程中的对流和扩散项计算需要用到变量的梯度。Fluent使用以下方法计算梯度：

• Green-Gauss Cell-Based
• Green-Gauss Node-Based
• Least Squares Cell-Based

3.1 Green-Gauss定理

当使用格林-高斯定理计算单元格中心处的标量的梯度时，将下面的离散形式写为

其中是网格面心处的值。

3.2 Green-Gauss Cell-Based方法

默认情况下，上式中的面值取自相邻网格中心处的值的算术平均值，即有：

3.3 Green-Gauss Node-Based方法

另一种方法，可以通过面节点值的算术平均值来计算：

式中，为面节点数量。

节点值(上式中的)由节点周围的网格值的加权平均值构成，遵循最初由Holmes和Connel^[6]和Rauch等^[7]人提出的方法。该方法通过求解一个约束极小化问题，在任意非结构网格上从周围的网格中心值重构节点处的线性函数的精确值，同时保持了二阶空间精度。

注：Green-Gauss Node-Based梯度方法比Green-Gauss Cell-Based梯度方法更精确，特别是在不规则(倾斜和扭曲)的非结构网格上，然而，它的计算成本比Green-Gauss Cell-Based梯度方法要高。

”

在密度基求解器中，基于节点梯度方法的稳定性可能会因为计算域边界上存在四面体网格而降低。要在四面体网格和混合网格上重新获得稳健性，建议选择TUI命令激活提供的基于节点的扩展边界选项：

solve/set/nb-gradient-boundary-option? yes yes

3.4 Least Squares Cell-Based方法

在这种方法中，假定解是线性变化的。如下图所示，网格和之间的单元值沿从网格的中心到网格的矢量变化，可以表示为：

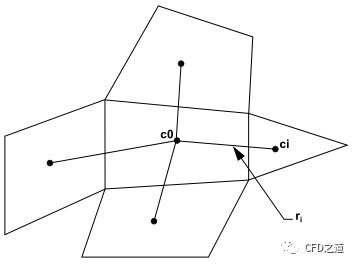
如果为网格周围的每个网格写出类似的方程式，就会得到以下以紧凑形式写成的系统：

式中，是纯几何函数的系数矩阵。

这里的目的是通过求解非平方系数矩阵在最小二乘意义下的最小化问题来确定网格梯度(通过求解最小二乘意义下的非平方系数矩阵系统的最小化问题)。

上述线性方程组是超定的，可以通过使用Gram-Schmidt过程^[8]分解系数矩阵来求解。这种分解为每个网格产生一个权重矩阵。因此对于以网格为中心的方法，这意味着为网格c0的每个面生成权重()的三个分量。

因此，然后可以通过将权重因子乘以差向量来计算单元格中心处的梯度：

在不规则(倾斜和扭曲)的非结构网格上，Least Squares Cell-Based梯度法的精度与Green-Gauss Node-Based梯度法相当(两者都比Least Squares Cell-Based梯度法好得多)。然而与Green-Gauss Node-Based梯度法相比，Least Squares Cell-Based梯度的代价更低。因此其被选为 Fluent求解器中的默认梯度方法。

4 梯度限制器

梯度限制器（Gradient limiters）也称为斜率限制器，常用于二阶迎风(SOU)格式以防在流场中激波、不连续或快速局部变化的局部流场中会出现虚假振荡。梯度限制器试图通过禁止网格面上的线性重构的场变量超过相邻单元的最大值或最小值来调用和实施单调性原则。

Fluent中有三种梯度限制器：

• Standard limiter
• Multidimensional limiter
• Differentiable limiter

梯度限制器可以分为两大类：不可微分限制器和可微分限制器。Standard限制器和多Multidimensional限制器都是不可微形式，它们使用最小和最大值类型的函数来限制解变量。Fluent中的第三个限制器，顾名思义是一种可微类型的限制器，其使用平滑函数来强加单调性。

对于上述每种限制器方法，Fluent提供了两个限制方向：

• 网格至网格面限制，其中重建梯度的极限值在网格面中心确定。这是默认方法。
• 网格至网格限制，其中重构梯度的限制值沿着两个相邻网格质心之间的缩放线确定。在正交网格上(或者当网格到网格方向平行于面区域方向时)，该方法与默认的网格至网格面方法等效。对于平滑物理场的变化，网格间的限制可以在具有倾斜的网格上提供较少的数值耗散。

注意，在非结构化网格上，Fluent使用以下公式给出的梯度限制器的标量形式：

式中，为梯度的限制值。

4.1 Standard Limiter

Standard 限制器是Fluent中的默认限制器函数，源自Barth和Jespersen^[9]的工作。该限制器是一种不可微分型的限制器，使用Minmod函数(最小模数)来限制和修剪网格面上的重建解、过冲和欠冲。

4.2 Multidimensional Limiter

Fluent中的Multidimensional 限制器^[10]具有与标准限制器相似的形式。由于多Multidimensional 限制器使用Minmod函数来限制梯度，因此它也被分类为不可微类型的限制器。然而，在Standard 限制器格式中，如果在网格的任何表面上进行限制，则这将导致网格梯度在所有方向上以相同的方式被修剪，而不管是否需要在其他网格表面上进行限制。这种限制方法是相当严格的，并且给数值格式增加了不必要的耗散。另一方面，Multidimensional 限制器试图通过仔细检查每个网格上的梯度并仅将梯度的法线分量修剪到网格表面来减轻梯度限制的严重程度。为了在标量形状限制器上工作，首先按大小升序排序网格面上的渐变的法线分量，以便只能应用必要的裁剪。因此，Multidimensional 限制器比标准限制器的耗散小。

4.3 Differentiable Limiter

不可微限制器的一个缺点是:在残差降低几个数量级后，它们往往会阻碍表观残差的收敛。请注意，这并不意味着求解不收敛，而是在残差部分停滞不前时求解继续收敛。这种恼人的行为可以直接追溯到限制函数的不可微性质。因此，可微限制器使用光滑函数来施加单调性条件，同时允许残差收敛。Fluent中使用的可微限制器是由Venkatakrishnan^[11]最初提出的限制器的改进形式^[12]。

注意：Fluent使用梯度或斜率限制器，而不是通量限制器。梯度限制器应用于网格面上线性重构的可变物理场的梯度，而通量限制器用于系统通量。

参考文献