本文简单描述Fluent对于网格的需求。

网格的质量对数值计算的准确性和稳定性起着重要作用。无论计算域中使用何种类型的网格，检查网格的质量都是必不可少的。Fluent 允许用户检查的网格质量的一个重要指标是正交性。为了确定给定网格的正交性，为每个网格面计算以下量：

• 网格面的面积向量与从网格中心到该面中心的向量的归一化点积

• 面的面积向量 ( ) 与从网格中心到共享该面的相邻网格中心的向量 ( ) 的归一化点积：

对网格的所有面应用上面的公式进行计算，取最小值作为该网格的正交性。因此最差网格的正交性更接近 0，而最好网格的正交性更接近 1。

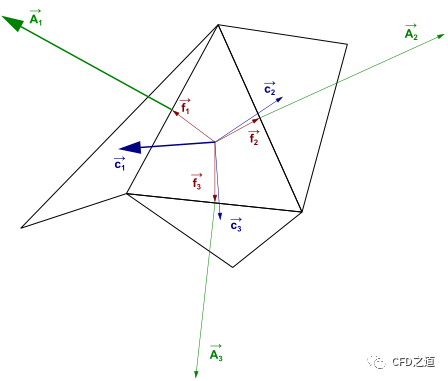
正交性的计算用于（但不总是等于）度量正交质量orthogonal quality。默认情况下，正交质量取决于网格类型：

• 对于四面体网格、三棱柱网格及金字塔网格，正交质量为正交性和（1-网格歪斜度）的最小值
• 对于六面体与多面体单元，正交质量与正交性相同

可以使用TUI命令mesh/enhanced-orthogonal-quality?对正交质量进行增强定义。启用此命令后，正交质量使用各种质量度量方式来定义，包括：网格面相对于从网格中心到面中心及相邻网格中心的向量的正交性；度量局部边缘不良的网格形状（例如扭曲和/或凹度）；度量网格面之间的法向变化。这种增强的定义是评估薄棱柱网格的最佳选择。

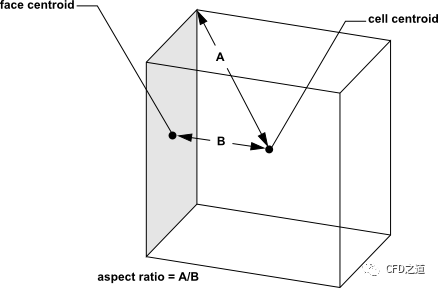
网格质量的另一个重要指标是长宽比（aspect ratio）。长宽比用于度量网格的拉伸程度，其被计算为以下距离的最大值与最小值之比：网格中心与面中心之间的法向距离（计算为距离向量和面法向的点积），以及网格中心与网格节点之间的距离。对于立方体，最大距离为 0.866，最小距离为 0.5，因此长宽比为 1.732。这种类型的定义可用于包括多面体在内的任何类型的网格。

要在Fluent中检查网格质量，可以在General任务页面中点击Report Quality按钮，控制台窗口中会输出网格质量相关信息，例如以下示例：

Mesh Quality:
Orthogonal Quality ranges from 0 to 1, where values close to 0 correspond to low quality.
Minimum Orthogonal Quality = 6.07960e-01
Maximum Aspect Ratio = 5.42664e+00

如果想了解更多控制台中显示的质量的信息（包括其他质量指标和具有最低质量网格的区域），可以在点击Report Quality按钮之前设置TUI命令 mesh/checkverbosity的值为 2（有效值为 0、1、2）。

可以右键选择模型树节点Cell Zone Condtions → ，点击弹出菜单项Info获得有关每个网格区域的网格数量和网格质量的信息，这种方式可以诊断哪个网格区域包含劣质网格。还可以对单个网格区域执行相同的Info检查。

有关如何改进劣质网格的信息，请参阅Repairing Mesh部分的描述。有关当具有靠近双侧壁面附近具有低质量面正交性网格时如何壁面发散的信息，可以参阅Orthogonality-Based Secondary Gradient Limiting at Coupled Two-Sided Walls部分的描述。

在评估网格质量是否足以解决正在模拟的问题时，最重要的是要考虑网格单元分布、网格形状、网格平滑度及流场依赖性等属性。这些属性将在以下部分中描述。

1 网格单元分布

由于连续区域被离散地定义，因此流动的显著特征（如剪切层、分离区域、激波、边界层和混合区等）的分辨率取决于网格元素的密度及分布。在许多情况下，关键区域的网格分辨率不佳会极大地影响计算结果。例如逆压梯度的分离预测在很大程度上取决于分离点上游边界层的分辨率。

边界层的分辨率（即壁面附近的网格距离）对壁面剪切应力和传热系数的计算准确性也起着重要作用。这在层流流动中尤其如此，在层流流动中，邻近壁面的网格应服从：

式中，为相邻网格中心到壁面的距离；为自由流的速度；为流体的运动粘度；为边界层起点沿壁面的距离。

湍流网格的分辨率也非常重要。由于平均流和湍流的强相互作用，湍流的数值结果往往比层流的数值结果更容易受到网格分布的影响。在近壁面区域，根据所使用的近壁面模型的不同而需要不同的网格分辨率。

一般情况下，任何流动通道内都不应少于 5 个网格，大多数情况下需要更多的网格来充分解决流动问题。在大梯度区域，如剪切层或混合区，网格应该足够精细，以尽量减少网格之间流动变量的变化。然而不幸的是，用户很难提前确定重要流动特征所在的位置。此外大多数复杂 3D 流场中的网格分辨率受到 CPU 时间和计算机资源（即内存和磁盘空间）的限制。尽管网格越多精度越高，但计算求解和后处理结果的对CPU 和内存需求也会增加。自适应网格细化可用于根据不断变化的流场增加和/或减少网格密度，因此可以更经济地使用网格（从而减少时间和资源需求）。

2 网格质量

网格的质量（包括其正交质量、长宽比和歪斜度）也对数值解的准确性有重大影响。

• 正交质量（Orthogonal quality）。如前面所述方法计算正交质量。最差网格的正交质量接近0，最佳网格接近1。所有类型网格的最小正交质量应大于0.01，且平均值应远高于0.01。

• 长宽比（Aspect ratio）。对于高度各向异性的流动，极端的长宽比也可能会以更少的网格产生准确的结果（如边界层内的流动）。一般来说，在流场出现较大变化或梯度较强的区域，最好避免网格长宽比突然发生较大的变化。

• 歪斜度（Skewness)。歪斜度定义为网格形状与等效体积的等边网格形状之间的差异。高度倾斜的网格会降低精度并使计算不稳定。例如，最佳的四边形网格具有接近 90 度的顶角，而三角形网格应优选具有接近 60 度的角并且所有角都小于 90 度。一般规则是，大多数流动中三角形/四面体网格的最大歪斜度应保持在 0.95 以下，平均值应明显低于该值。歪斜度大于 0.95 的网格可能会导致收敛困难，并且可能需要更改求解器控制参数，例如降低欠松弛因子和/或切换到压力基耦合求解器。

网格尺寸变化和网格面翘曲也是可能影响计算稳定性和准确性的额外质量度量。

3 网格平滑度

截断误差是控制方程中的偏导数与其离散近似值之间的差异。相邻网格之间网格体积的快速变化会导致更大的截断误差。Fluent 能够通过基于网格体积变化或网格体积梯度对网格进行细化，从而提高网格平滑度。在网格生成过程中，通常使用变化率来控制网格平滑度，该参数一般控制在1.1~1.3为宜，有一些网格生成软件默认该参数为1.5，不建议用太大的比率值。

4 流场依赖

网格分辨率、平滑度和网格形状对计算准确性和稳定性的影响取决于所模拟的流场。例如，在梯度较小的流动区域内可以容忍非常扭曲的网格，但在流动梯度很强的区域中扭曲的网格可能是非常有害的。由于流动梯度大的位置在计算之前通常无法确定，因此应该努力在整个流动域上实现高质量的网格。

（完）