源地址：http://hassankassem.me/posts/ode/。作者：Hassan Kassem

本文描述如何利用OpenFOAM求解常微分方程。

本文并非要对每个常微分方程（ODE）求解器进行全面的回顾或解释，而是一步一步地展示如何定义一个ODE，以及如何编写一个小程序来求解此ODE。

1 数学背景

为了利用数值方法求解高阶常微分方程，可以其简化为一阶常微分方程组进行求解。降阶产生的常微分方程中方程的数量等于原始常微分方程的阶数。

一般的常微分方程可以表示为：

式中，为导数阶数。

可以将式（1）转化为：

最后，常微分方程可以表示为以下的形式：

转换过程可概括为两个步骤；变量转换及微分。

在OpenFOAM中求解ODE，刚性求解器额外需要雅可比矩阵和时间偏导数。

雅克比矩阵如下：

其中是简化系统中的方程式。及其关于自变量的偏导数：

2 例子：运动方程

这里以单自由度系统（简单质量-弹簧系统）的运动方程为例，其为一个二阶常微分方程：

式中，为质量，为刚度，为位移。

该方程有一个精确解，表示系统的谐波振荡为（假设初始速度为零）；

式中，为初始位移，为系统的固有频率，。

求解此方程的分为三步：

1. 将转化为

2. 微分（先替换）

则有：

3. Jacobian

雅克比矩阵仅用于刚性求解器。对于这里的微分方程，其雅克比矩阵为矩阵：

时间导数为：

3 程序设计

在OpenFOAM中，典型的做法是搜索类似的实现作为起点。幸运的是，OpenFOAM源文件中包含了一个小测试程序。所以将其复制到运行目录，然后编译并运行它。（RKCK45是OpenFOAM ODE解算器之一）。

3.1 准备文件

运行一下命令：

run
mkdir myODE
cd myODE
cp -r $FOAM_APP/test/ODE .
cd ODE

ODE文件夹中包含一个Make文件夹以及一个名为Test-ODE.C的源文件。

编译源文件并测试运行：

wmake
Test-ODE RKCK45

如下图所示表示编译且运行成功。

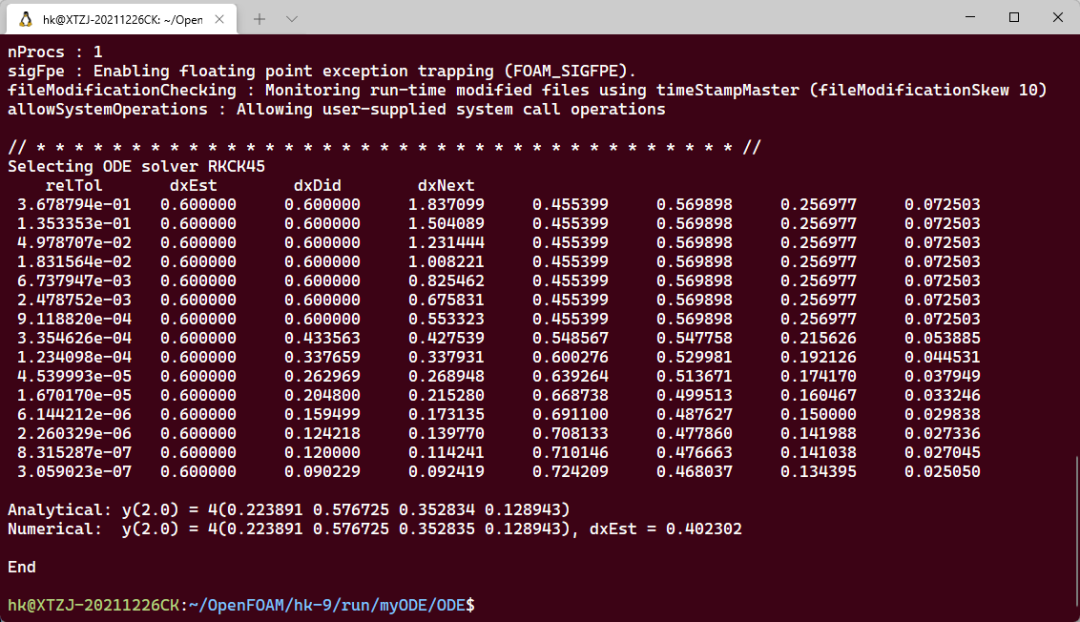
注：这里的RKCK45为四阶-五阶Cash-Karp Runge-Kutta法。除该算法外，OpenFOAM还提供了  SIBS, Rosenbrock34, RKF45, RKDP45, rodas34, rodas23, Rosenbrock23, Rosenbrock12, EulerSI, Euler, 及 Trapezoid等算法，有兴趣的话可以自行尝试。

”

3.2 修改源文件

修改Test-ODE.C文件，如下所示。

#include "argList.H"
#include "IOmanip.H"
#include "ODESystem.H"
#include "ODESolver.H"
using namespace Foam;

// * * * * * * * * * * * * * * * * * * * * * * * * //
class testODE
    : public ODESystem
{

public:
    // 质量
    const scalar m_;
    // 刚度系数
    const scalar k_;
    testODE(const scalar &mass, const scalar &stiff) : ODESystem(),
                                                       m_(mass),
                                                       k_(stiff)
    {
    }

    label nEqns() const
    {
        return 2;
    }
        
	// 必须实现的虚函数，计算导数，与原文有差异
    void derivatives(
        const scalar x,
        const scalarField &y,
        const label li,
        scalarField &dydx) const
    {
        dydx[0] = y[1];
        dydx[1] = -(k_ / m_ + VSMALL) * y[0];
    }
        
	// 必须实现的虚函数，计算雅克比矩阵，与原文有差异
    void jacobian(
        const scalar x,
        const scalarField &y,
        const label li,
        scalarField &dfdx,
        scalarSquareMatrix &dfdy) const
    {
        dfdx[0] = 0.0;
        dfdx[1] = 0;
        
        dfdy(0, 0) = 0.0;
        dfdy(0, 1) = 1.0;
        
        dfdy(1, 0) = -(k_ / m_ + VSMALL);
        dfdy(1, 1) = 0;
    }
};

// * * * * * * * * * * * * * * * * * * * //

int main(int argc, char *argv[])
{
    argList::validArgs.append("ODESolver");
    argList args(argc, argv);

    // 指定质量与刚度系数
    const scalar mass = 2.0;
    const scalar stiff = 2048.0;

    // 指定初始条件
    const scalar y0 = 0.2;
    const label n = 200;
    const scalar endTime = 1.0;

    // 创建ODE对象
    testODE ode(mass, stiff);
    
    dictionary dict;
    dict.add("solver", args[1]);
    
    autoPtr odeSolver = ODESolver::New(ode, dict);

    scalar xStart = 0.0;
    const scalar dx = endTime / n;
    scalarField yStart(ode.nEqns());
    yStart[0] = y0;
    yStart[1] = 0.0;
    scalar dxEst = 0.1;
    scalar xEnd = 0.0;
    label li =1;
    scalarField dyStart(ode.nEqns());

    for (label i = 0; i < n; i++)
    {
        xEnd = xStart + dx;
        ode.derivatives(xStart, yStart, li, dyStart);
        odeSolver->solve(xStart, xEnd, yStart, li, dxEst);
        xStart = xEnd;
        Info << xStart << "     " << yStart[0] << endl;
    }
    Info << "n Endn"
         << endl;
    return 0;
}

• 运行命令编译源代码：

wmake

如下图所示表示编译成功。

• 运行以下命令执行程序

Test-ODE RKCK45 > log

• 启动gnuplot执行以下命令

mass = 2.0
stiff = 2048.0
x0 = 0.2

set grid
set samples 200
set xlabel 'Time (s)'
set ylabel 'Displacement (m)'
set yrange [-0.3:0.3]

f(x) = x0*cos(sqrt(stiff/mass)*x)
plot 'log' u 1:2 w p lw 2 t "OpenFOAM", f(x) w l lw 2 t "Exact"

结果如下图所示。数值解与解析解吻合良好。

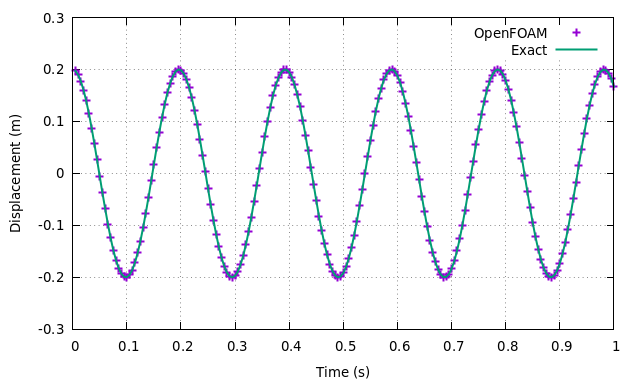
利用OpenFOAM中自带的ODE求解器还是蛮麻烦的，像上面简单的二阶常微分方程，利用matlab只需要几行程序就能搞定。

（本文结束）