本文描述在OpenFOAM中编程实现自定义边界类型。

OpenFOAM中可以利用codeStream、codeFixedValue实现自定义边界上物理场分布。这些方式操作起来简单，但是功能也较为单一。若想要实现更加复杂的边界条件类型，可以通过编程创建新的边界类型。

OpenFOAM中所有的边界条件定义均位于文件夹$FOAM_SRC/finiteVolume/fields/fvPatchFields中，用户可以利用文件夹中的边界类型为模板，开发自己的边界条件类型。

以一个沿y方向速度成抛物线分布的边界为例，描述在OpenFOAM中新建一个边界条件的基本流程。在充分发展的管道流动中，轴向速度沿径向分布为：

这里为平均速度；为径向方向坐标，为管道半径，为圆心坐标。

1 文件准备

打开Linux终端或Windows WSL，通过下面的命令准备文件。

run
foamNewBC -f -v parabolicVelocity
cd parabolicVelocity

这里利用程序foamNewBC快速构造一个边界条件定义框架。关于foamNewBC的用法，可以使用命令foamNewBC -help进行查看，如下图所示。

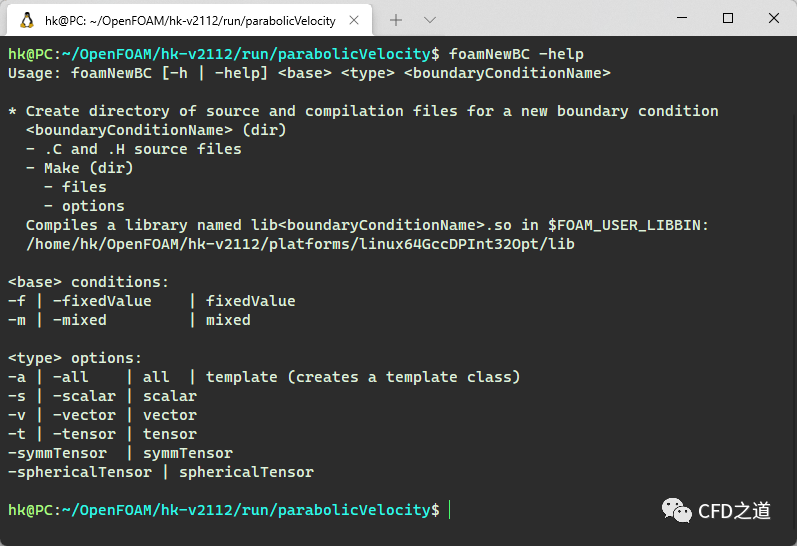
上面的命令中，-f表示创建一个fixedValue型边界；-v表示创建一个矢量边界。

此时在当前路径下创建了一个名为parabolicVelocity的文件夹，其内文件结构如下图所示。

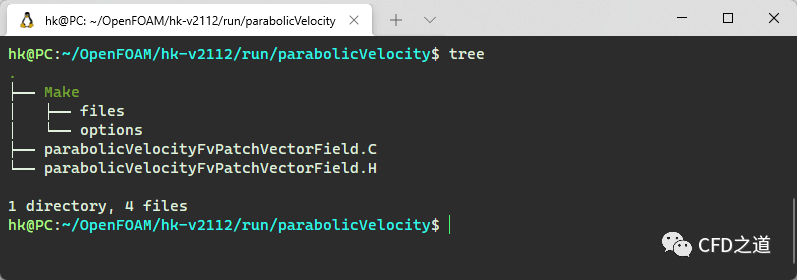
文件夹parabolicVelocity中包含了一个Make文件夹与parabolicVelocityFvPatchVectorField.C及parabolicVelocityFvPatchVectorField.H文件。这里不需要改动Make文件夹中的任何内容。

2 修改头文件

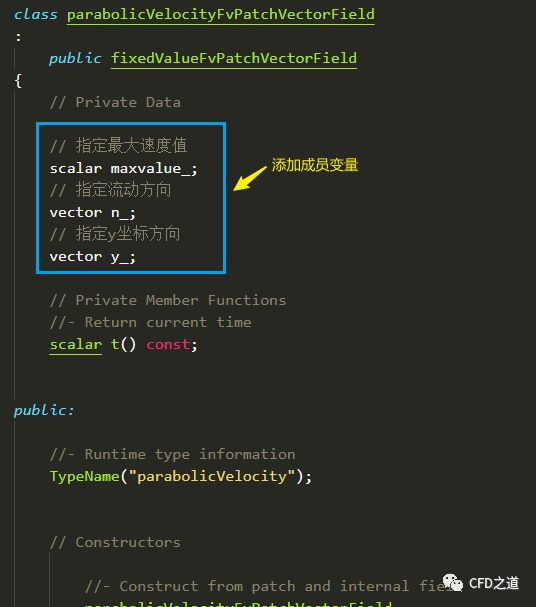
在头文件parabolicVelocityFvPatchVectorField.H中指定成员变量及构造函数。

• 删除多余的成员变量，添加新的成员变量

// 指定最大速度值
scalar maxvalue_;
// 指定流动方向
vector n_;
// 指定y坐标方向
vector y_;

如下图所示。

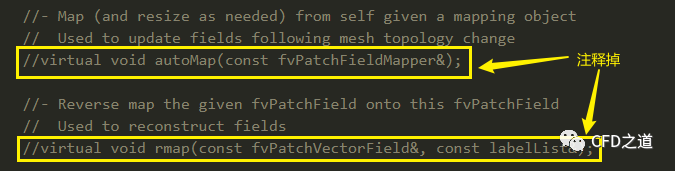
• 注释掉虚函数autoMap与rmap的定义

3 修改源文件

在源文件parabolicVelocityFvPatchVectorField.C中定义功能实现。

• 注释或删掉t()函数
• 在第一个构造函数中添加参数初始化程序代码

// 默认初始化
Foam::parabolicVelocityFvPatchVectorField::
    parabolicVelocityFvPatchVectorField(
        const fvPatch &p,
        const DimensionedField<vector, volMesh> &iF)
    : fixedValueFvPatchVectorField(p, iF),
      maxvalue_(0),
      n_(1, 0, 0),
      y_(0, 1, 0)
{
}

• 修改第二个构造函数

Foam::parabolicVelocityFvPatchVectorField::
parabolicVelocityFvPatchVectorField
(
    const fvPatch& p,
    const DimensionedField<vector, volMesh>& iF,
    const dictionary& dict
)
:
    fixedValueFvPatchVectorField(p, iF),
    maxvalue_(readScalar(dict.lookup("maxvalue"))),
    n_(dict.lookup("n")),
    y_(dict.lookup("y"))
{
    Info << "Using the parabolicVelocity boundary condition" << endl;
    if (mag(n_) < SMALL || mag(y_) < SMALL)
    {
        FatalErrorIn("parabolicVelocityFvPatchVectorField(dict)")
        << "n or y given with zero size not correct"
        << abort(FatalError);
    }
    n_ /= mag(n_);
    y_ /= mag(y_);
 
    fixedValueFvPatchVectorField::evaluate();
}
 

• 修改第三个构造函数

Foam::parabolicVelocityFvPatchVectorField::
    parabolicVelocityFvPatchVectorField(
        const parabolicVelocityFvPatchVectorField &ptf,
        const fvPatch &p,
        const DimensionedField<vector, volMesh> &iF,
        const fvPatchFieldMapper &mapper)
    : fixedValueFvPatchVectorField(ptf, p, iF, mapper),
      maxvalue_(ptf.maxvalue_),
      n_(ptf.n_),
      y_(ptf.y_)
{
}

• 修改第四个构造函数

Foam::parabolicVelocityFvPatchVectorField::
    parabolicVelocityFvPatchVectorField(
        const parabolicVelocityFvPatchVectorField &ptf)
    : fixedValueFvPatchVectorField(ptf),
      maxvalue_(ptf.maxvalue_),
      n_(ptf.n_),
      y_(ptf.y_)
{
}

• 修改第五个构造函数

Foam::parabolicVelocityFvPatchVectorField::
    parabolicVelocityFvPatchVectorField(
        const parabolicVelocityFvPatchVectorField &ptf,
        const DimensionedField<vector, volMesh> &iF)
    : fixedValueFvPatchVectorField(ptf, iF),
      maxvalue_(ptf.maxvalue_),
      n_(ptf.n_),
      y_(ptf.y_)
{
}

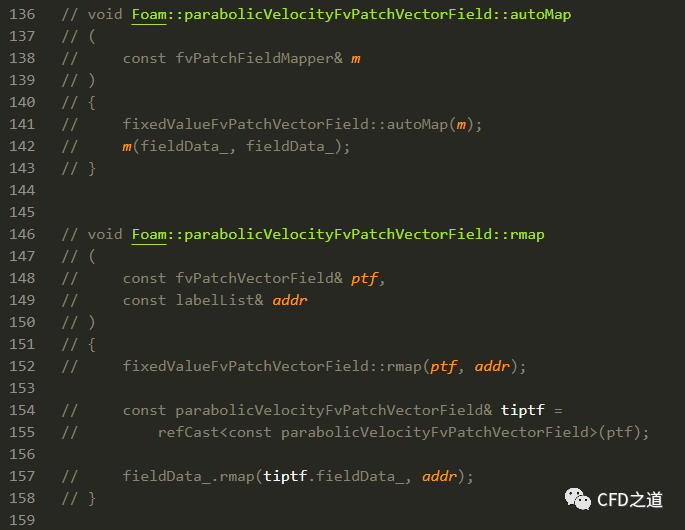
• 删除aotuMap及rmap函数

这里直接将这两个函数给注释掉。

• 修改updateCoeffs()函数

抛物线边界的功能实现是在函数updateCoeffs()中完成的。修改其函数内容：

// updateCoeffs函数用于指定边界上的物理场分布
// 此函数是核心函数，所有的功能均在此实现
void Foam::parabolicVelocityFvPatchVectorField::updateCoeffs()
{
    if (updated())
    {
        return;
    }
  // 得到边界坐标
    boundBox bb(patch().patch().localPoints(),true);
    // 得到边界的中点，因为并非所有时候中点都是零
    vector ctr = 0.5*(bb.max()+bb.min());
    // 得到面向量
    const vectorField &c = patch().Cf();
  // 这里的&符号表示向量点积
    scalarField coord = 2*((c-ctr)&y_)/((bb.max()-bb.min())&y_);
    // 给边界赋值
    vectorField :: operator =(n_*maxvalue_ * (1.0-sqr(coord)));
    
    fixedValueFvPatchVectorField::updateCoeffs();
}

• 修改write函数

// write函数利用Ostream对象将参数写入到文件中
void Foam::parabolicVelocityFvPatchVectorField::write
(
    Ostream& os
) const
{
    fvPatchVectorField::write(os);
    writeEntry(os,"n",n_);
    writeEntry(os,"y",y_);
    writeEntry(os,"maxvalue",maxvalue_);
    writeEntry(os,"value", *this);
}

这里注意writeEntry的调用方式，原文中的写法在新版OpenFOAM中会编译出错。

• 保存源文件。

4 编译源文件

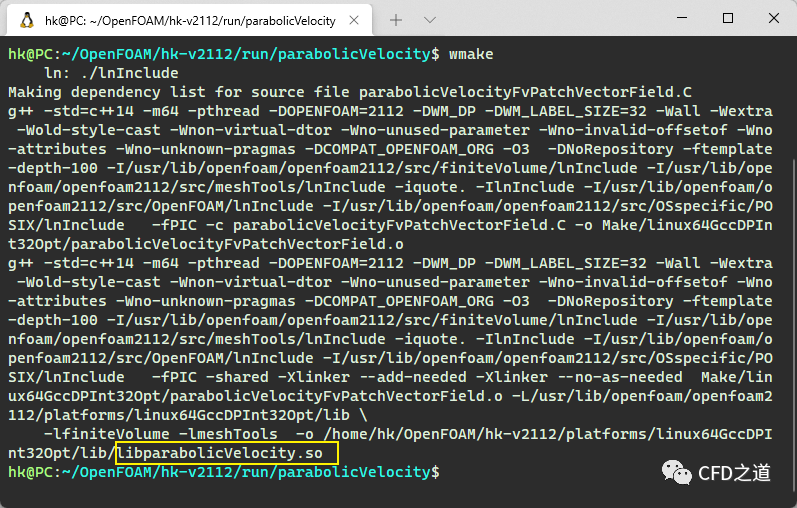
进入到源代码路径，执行下面的命令进行编译。

wmake

如果没有问题的话，编译完成后终端显示如图所示。

5 测试

利用算例库中的pitzDaily算例进行测试。利用下面的代码拷贝文件。

run
cp -r $FOAM_TUTORIALS/incompressible/simpleFoam/pitzDaily pitzDailyParabolicInlet
cd pitzDailyParabolicInlet/

• 修改0/U文件

修改边界inlet的参数：

inlet
{
    type            parabolicVelocity;
    n               (1 0 0);
    y               (0 1 0);
    maxvalue        2;
}

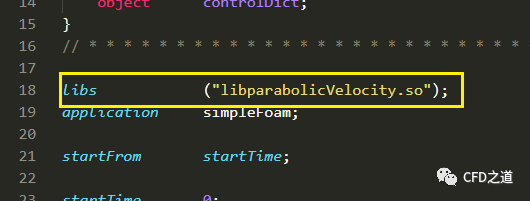
• 修改system/controlDict文件

添加语句libs ("libparabolicVelocity.so");，如下图所示。

• 进行计算

blockMesh
simpleFoam

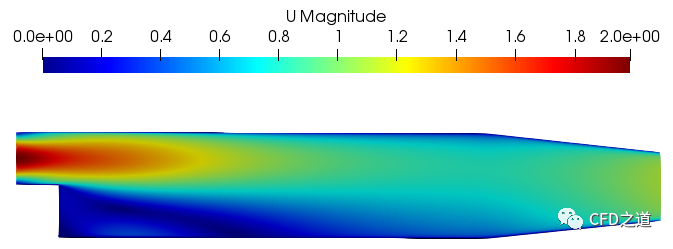
• 计算结果

速度分布如下图所示。

入口速度分布曲线如下图所示。

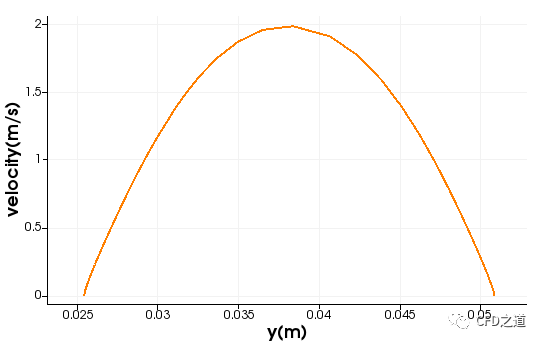
可以看到入口速度是按照要求成抛物线分布。

（完毕）