本案例演示利用OpenFOAM中的基础代码实现SIMPLE算法。

1 SIMPLE算法

对于不可压缩NS方程，可以表示为：

式中有4个待求物理量：。式中为运动压力()，为运动粘度。

方程求解有两个麻烦问题需要处理：

• 没有显式的压力求解方式。压力隐藏在动量方程中，与速度耦合在一起
• 动量方程的求解受到连续方程的约束，即从动量方程中求解得到的速度不一定能够满足连续方程

SIMPLE算法采用下面的步骤进行处理：

1. 将动量方程写成矩阵方程的形式

式中，矩阵为利用有限体积法离散得到的方程系数矩阵。矩阵方程展开成下面的样子：

矩阵的元素可以从任何一本CFD教材中得到。

2. 将矩阵写成下面的形式

其中矩阵为矩阵的对角矩阵，即：

将式(5)代入式(3)，可得到：

式(7)可以得到：

将式(8)代入连续方程式(1)可得到：

挪一下位置，式(9)可以写成下面的形式：

方程(10)常被称为压力poisson方程，求解此泊松方程可以得到压力场。

得到压力场数据后利用式(8)计算速度场，之后反复迭代计算，直到残差达到要求。

SIMPLE算法计算过程中涉及到的一些矩阵包括：

• 矩阵
• 矩阵

由于矩阵为对角矩阵，因此其逆矩阵可以很容易计算得到：

• 矩阵

2 程序实现

利用OpenFOAM中的基础代码实现Simple算法。

2.1 文件准备

利用下面的命令创建文件。

run
foamNewApp SIMPLEdemo
cd SIMPLEdemo
touch createFields.H

程序文件结构如下图所示。

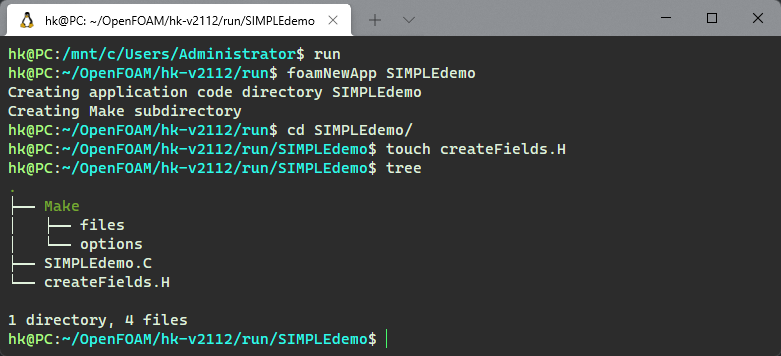
2.2 程序代码

这里采用的是foamNewApp创建的程序文件结构，因此Make文件夹中的内容保持默认即可。

• 头文件createFileds.H包含物理量的准备

 
Info << "读取压力场" << endl;
volScalarField p
(
    IOobject
    (
        "p",
        runTime.timeName(),
        mesh,
        IOobject::MUST_READ,
        IOobject::AUTO_WRITE
    ),
    mesh
);
 
// 定义一个标量p_old，用于存储迭代前的压力
volScalarField p_old
(
    IOobject
    (
        "p_old",
        runTime.timeName(),
        mesh,
        IOobject::NO_READ,
        IOobject::NO_WRITE
    ),
    p
);
 
// 读取速度场U
Info << "读取速度场U" << endl;
volVectorField U
(
    IOobject
    (
        "U",
        runTime.timeName(),
        mesh,
        IOobject::MUST_READ,
        IOobject::AUTO_WRITE
    ),
    mesh
);
 
// 定义通量场phi
Info << "创建通量场" << endl;
surfaceScalarField phi
(
    IOobject
    (
        "phi",
        runTime.timeName(),
        mesh,
        IOobject::NO_READ,
        IOobject::AUTO_WRITE),
    //默认值设置为边界面速度向量插值与面积向量点击
    fvc::interpolate(U) & mesh.Sf()
);
 
// 读取输运参数
IOdictionary transportProperties
(
    IOobject
    (
        "transportProperties",
        runTime.constant(),
        mesh,
        IOobject::MUST_READ_IF_MODIFIED,
        IOobject::NO_WRITE
    )
);
 
dimensionedScalar nu
(
    "nu",
    dimViscosity,
    transportProperties
);
 
// 定义一个字典变量，用于参考压力的读写
IOdictionary fvSolution
(
    IOobject
    (
        "fvSolution",
        runTime.system(),
        mesh,
        IOobject::MUST_READ_IF_MODIFIED,
        IOobject::NO_WRITE
    )
);
 

• 编写源文件SIMPLEdemo.C

#include "fvCFD.H"
 
int main(int argc, char *argv[])
{
    // 检查案例文件结构
    #include "setRootCase.H"
    // 创建Time对象runTime
    #include "createTime.H"
    // 创建fvMesh对象mesh
    #include "createMesh.H"
    //包含前面定义的头文件
    #include "createFields.H"
 
    // 亚松弛因子alpha，从fvSolution字典文件中读取
    scalar alpha;
    fvSolution.lookup("alpha") >> alpha;
    // 参考压力所指定的网格
    scalar pRefCell;
    fvSolution.lookup("pRefCell") >> pRefCell;
    // 参考压力值
    scalar pRefValue;
    fvSolution.lookup("pRefValue") >> pRefValue;
 
    // 试着将读取的值输出到控制台（没什么用，可选）
    Info << nl << "读取了以下参数：" << endl;
    Info << "亚松弛因子alpha = " << alpha << endl;
    Info << "参考压力网格索引：" << pRefCell << endl;
    Info << "参考压力值：" << pRefValue << endl;
 
    // 主循环
    while (runTime.loop())
    {
        Info << nl << "Iteration：" << runTime.timeName() << endl;
        // 定义动量方程
        fvVectorMatrix UEqn(
            fvm::div(phi, U) - fvm::laplacian(nu, U) == -fvc::grad(p));
        // 利用当前的压力场数据求解动量方程，得到速度场
        UEqn.solve();
 
        // 动量方程写成矩阵方程为M*U=Nab(p),可以写成A*U-H=Nab(p)
        // 得到A矩阵和H矩阵，注意A矩阵为标量，H为矢量
        volScalarField A = UEqn.A();
        volVectorField H = UEqn.H();
 
        // 计算A矩阵的逆矩阵,A为对角矩阵，其逆矩阵等于1/A
        volScalarField A_inv = 1.0 / A;
 
        // 定义向量场HbyA = A_inv * H
        volVectorField HbyA = A_inv * H;
 
        // 定义通量场
        surfaceScalarField A_inv_flux = fvc::interpolate(A_inv);
 
        // 求压力泊松方程
        // 方程定义为Nab(A^-1 Nab(p)) = Nab.(A^-1 * H)
        fvScalarMatrix pEqn(
            fvm::laplacian(A_inv_flux, p) == fvc::div(HbyA));
        // 设置参考压力
        pEqn.setReference(pRefCell, pRefValue);
        // 求解方程
        pEqn.solve();
 
        // 对求解得到的压力进行亚松弛
        p = alpha * p + (1.0 - alpha) * p_old;
 
        // 根据新的压力场数据修正速度场U = A^-1 * H - A^-1 * Nab.(p)
        U = A_inv * H - A_inv * fvc::grad(p);
 
        // 更新通量phi
        phi = fvc::interpolate(U) & mesh.Sf();
 
        // 更新边界上的压力场与速度场
        U.correctBoundaryConditions();
        p.correctBoundaryConditions();
 
        // 更新旧压力场
        p_old = p;
 
        // 将得到的物理场写入到文件中
        runTime.write();
    }
 
    // * * * * * * * * * * * * * * * * * * * * * * //
    Info << nl << runTime.printExecutionTime(Info);
    Info << "Endn" << endl;
 
    return 0;
}
 

利用wmake编译程序，确保编译过程中没有错误信息，如下图所示。

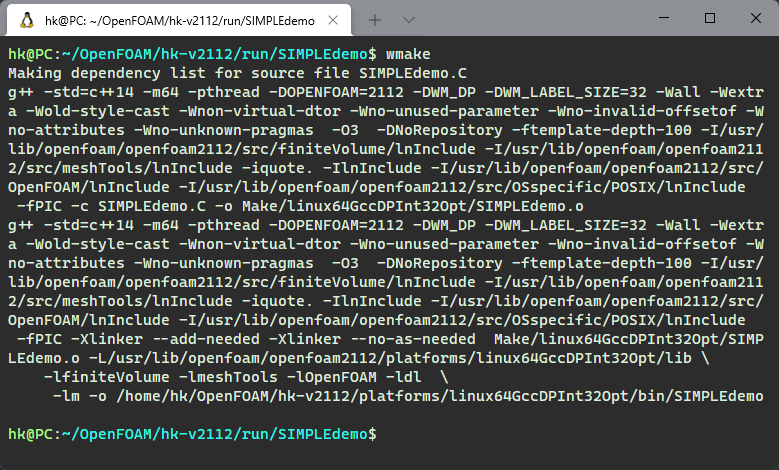
2.3 测试案例

案例采用2D计算模型，长度0.5 m，宽0.1 m，入口流速1 m/s，出口静压0 Pa，其他边界为无滑移壁面。案例的准备与常规案例基本相同，这里仅需要在fvSolution中添加程序中所需的关键字。

• system/fvSolution文件

FoamFile
{
    version     2.0;
    format      ascii;
    class       dictionary;
    location    "system";
    object      fvSolution;
}
// * * * * * * * * * * * * * * * * * * * //
solvers
{
    p
    {
        solver          PCG;
        preconditioner  DIC;
        tolerance       1e-06;
        relTol          0;
    }
 
    pFinal
    {
        $p;
        relTol          0;
    }
 
    U
    {
        solver          smoothSolver;
        smoother        symGaussSeidel;
        tolerance       1e-04;
        relTol          0;
    }
}
 
// 亚松弛因子
alpha 0.01;
// 定义参考压力的网格编号
pRefCell 99;
// 参考压力值
pRefValue 0;
 

计算结果如下图所示。

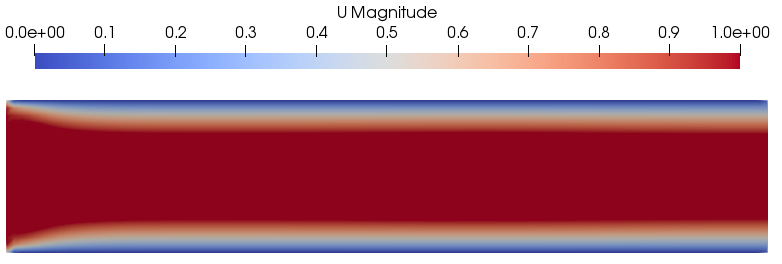
（本文完毕）