SRS模型｜02 LES模型工程应用局限

本文描述大涡模拟（Large Eddy Simulation，LES）应用的局限性。

为理解混合RANS/LES模型存在的原因，必须先了解大涡模拟(LES)的局限性。在过去的几十年中，LES一直是使用最为广泛的SRS模型。LES模型基于只解析大尺度湍流和模型化小尺度湍流的概念。LES 的经典动机是：大尺度取决于流动问题且难以模化，而小尺度变得越来越普遍及各向同性，可以更容易地被模化。

LES 在有限空间区域（通常是网格体积）上对Navier-Stokes方程进行过滤，旨在仅解析大于过滤器宽度的湍流部分，而对小于过滤器的湍流结构进行模化处理（通常采用简单的涡粘模型进行模化处理）。

LES中的过滤操作定义为：

式中，为空间过滤器。

Navier-Stokes 方程在过滤后会得到以下形式（忽略密度脉动）：

过滤操作使得方程具有额外的应力项：

尽管推导过程中存在差异，但额外的亚格子应力张量通常与RANS中使用的涡流粘度模型相同：

这种模拟方法的重要实际意义在于，如果在两种情况下都使用涡粘模型，则RANS和LES的动量方程是相同的。换句话说，Navier-Stokes方程对起推导一无所知。它们从湍流模型中得到的唯一信息是涡粘水平。根据这一点，方程将在RAN或LES模式(或某些中间模式)下运行。过滤后的Navier-Stokes方程与RANS方程具有一致的形式是混合RANS/LES湍流模型的基础。显然只需切换模型(和数值)即可将它们引入到同一组动量方程中。

经典的大涡模拟模型Smagorinsky(1963)模型的形式：

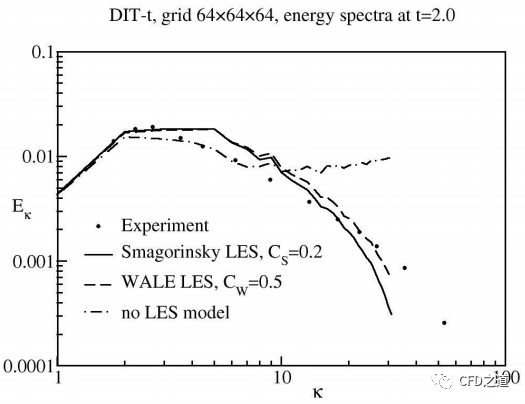
式中，为网格间距；为应变率标量； 为常数。这显然是一个相当简单的公式，表面LES模型无法提供最小尺度的高精度表示。从实际应用的角度来看，可能也并不需要非常详细的建模。LES更合适的目标不是模拟未解析尺度涡对已解析尺度涡的影响，而是模拟最小解析尺度涡的耗散。这可以从下图中看出，该图显示了衰减各向同性湍流的湍流能谱。 为湍流能量，其为波数  的函数。小  值表示大涡流，大值表示小涡流。湍流在湍流谱中从小波数向高波数移动。在完全解析的湍流模拟（直接数值模拟，DNS）中，湍流通过粘度在最小的尺度上耗散为热量。耗散量通过下式计算：

式中，为非常小的运动分子粘度。由于最小尺度的速度梯度很大，耗散仍然是有限值的。

然而，LES计算通常是在太粗而无法解析最小尺度的数值网格上执行的。在当前的例子中，大涡模拟的截止极限(分辨率极限)在k=10左右。大涡模拟中最小分辨尺度的速度梯度比DNS极限下的速度梯度要小得多，因此分子粘度不足以提供正确的耗散水平。在这种情况下，适当的耗散量可以通过增加涡粘度来实现：

涡粘度通过在LES网格极限下提供正确的耗散量来校准。可以在下图中看到效果，图中展示的是在没有LES模型和使用不同的LES模型的情况下执行DIT情况的LES。当 LES 模型被激活时能量被耗散，模式为所有分辨率的尺度提供了一个敏感的谱。换句话说，LES 并未模拟未解析的小尺度湍流对较大的已解析尺度的影响，而是将湍流耗散为热量（耗散的能量相对于流体的热能通常非常小，除了高马赫数流动外通常不必考虑。）

这一讨论表明，LES是一种相当简单的技术，其并不能提供可靠的建模骨架，即便是更复杂的LES模型(如Dynamic Models)也是如此。动态涡粘LES模型(见Guerts 2004)的设计目的是根据较大尺度(通常是过滤器宽度的两倍)的流动条件来估计网格极限下所需的耗散水平，从而减少对模型校准的需要。然而，这样的模型也只能为能量耗散提供合适的涡粘度水平。因此在 LES 框架内，必须在空间和时间上求解工程师感兴趣和相关的所有流动特征和影响，这使得 LES 成为一项非常耗费 CPU 的技术。

更苛刻的是将 LES 应用于工程流动中的典型的壁面有界流。大涡的湍流长度尺度 可以表示为：

其中，为壁面距离；为常数。换句话说，即使是（局部）最大的尺度在壁面附近也变得非常小，并且在所有三个空间维度和时间上都需要高分辨率。

对  的线性相关性表明壁面附近的湍流长度尺度接近于零，因此这将需要一个无限精细的网格来求解湍流结构。然而实际情况并非如此，因为分子粘度会阻止小于 Kolmogorov 极限的尺度。这体现在粘性或层流子层上，这是一个非常靠近壁面的区域，在该区域湍流受到抑制，并不需要求解。然而，粘性子层的厚度是流动雷诺数 Re 的函数。在较高的 Re 数下，粘性子层变得越来越薄，从而允许越来越小的涡存在，而这些小涡都需要求解。

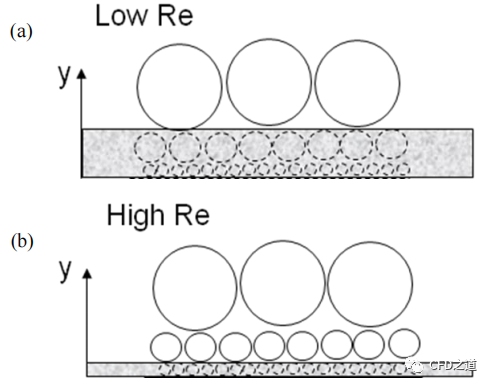
下图显示了壁面附近湍流结构的草图（如流向垂直于观察者的通道流）。图片的上半部分代表低 Re 数，下半部分代表较高 Re 数的情况。灰色框表示两个不同 Re 数条件下的粘性子层。粘性子层内的结构如灰色框内的圆圈所示。现实中并不存在粘性阻尼，只有粘性子层之外（即灰色框上方）的结构需要解析。由于高 Re 情况下粘性子层的厚度减小，因此需要更大的分辨率来解析所有激活的尺度。壁面解析LES 对于中到高雷诺数来说计算开销非常大，这是 LES 不适合大多数工程流动的主要原因。

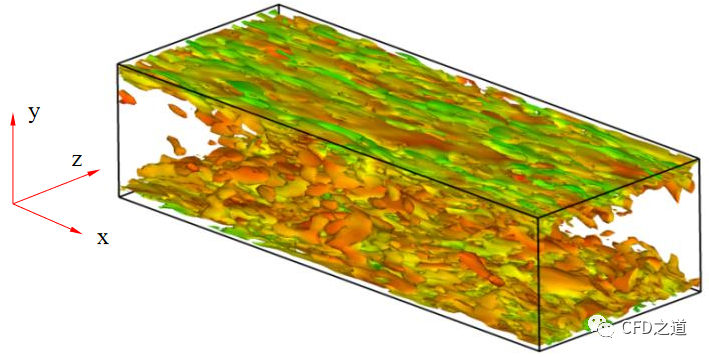
对于下图所示的简单周期性通道流，可以估计壁面解析LES的雷诺数依赖性(x-流动方向，y-壁面法线方向，z-展向方向，H-通道高度)。

LES的典型分辨率要求为：

式中，为流向方向上的无量纲网格间距；为展向方向的无量纲网格间距；为横跨半个通道高度的网格单元数量。根据定义有：

根据雷诺数的定义：

可得到三方向上网格数量：

对这个简单的流体域，需要的网格数量如下表所示。

基于体积速度的雷诺数 比基于摩擦速度的雷诺数大10倍左右。注意基于 h=H/2。网格单元的数量随着 Re 数的增加而急剧增加，即使对于非常简单的流体流动也需要大量的计算资源。另外还需要减少时间步长以保持恒定的 CFL 数（）。

通道流的 Re 数尺度可以通过应用壁面函数来减少，随着 Re 数的增加，y+值不断增加。然而，壁面函数是模型不确定性的重要来源，其会破坏模拟的整体准确性。此外，RANS 模型的经验表明，为复杂几何生成高质量的壁面函数网格是一项非常具有挑战性的任务。对于 LES 应用更是如此，用户必须控制所有三个空间维度的分辨率以符合 LES的需求。

对于外部流动，边界层的相对厚度(如相对于翼型弦长的边界层厚度)会产生额外的Re数效应。当雷诺数较高时，边界层相对于物体的尺寸变得非常薄。假设每个边界层体积的分辨率不变，Spalart(1997,2000)在最有利的假设下对高雷诺数空气动力流动的计算能力需求进行了估计。即便如此，计算资源需求仍然过多，除了简单的流动外，即使是对几十年的计算能力增长进行乐观估计，也无法满足这一要求。

虽然高 Re 数流的计算要求由相对薄的边界层主导，但低 Re 数流动的情况通常同样不利，因为层流-湍流转捩效应占主导地位，需要进行求解。基于叶轮机械叶片的简化几何模拟(例如Michelassi，2003)，下表给出了带有端壁的单个涡轮叶片的估计值：

考虑到透平机械公司的目标是整机(或至少是其中的重要部分)的模拟，假设大涡模拟将成为工业CFD模拟的主要元素是不现实的，即使对于如此低Re数(Re~1e5)的应用。但是，LES可以在对此类流动的组成部分(如冷却孔或主动流动控制)的详细分析中发挥作用。

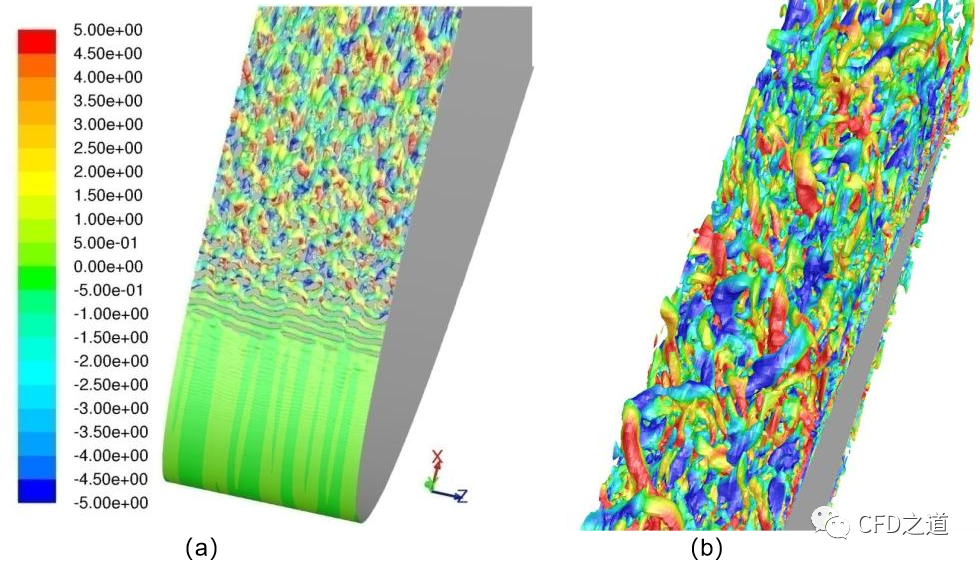
所有这些并不意味着壁面有界流动的大涡模拟完全不可行，只是这种模拟的成本很高。下图显示了在NACA 0012翼型周围使用Wale模型的大涡模拟所采用的计算网格。使用该方向的周期性边界条件，计算区域在展向方向上被限制在翼型弦长的5%范围内。在雷诺数Re=1.1e6时，估计了5%的跨度范围是允许湍流结构在不被周期边界条件同步的情况下发展的最小区域尺寸。这一估计是基于前置RANS计算得到的后缘边界层厚度。该边界层厚度约为2%弦长。网格在展向方向上有 80 个网格，总共有 11e6 个网格。在不可压缩模式下使用 Fluent 以 a=7.3° 的攻角进行模拟。弦长设置为 c=0.23 [m]，自由流速度 U=71.3 [m/s]，流体为标准条件下的空气。时间步长设置为 Dt= 1.5×10-6 [s]，在边界层内给出 CFL~0.8 的 Courant 数。

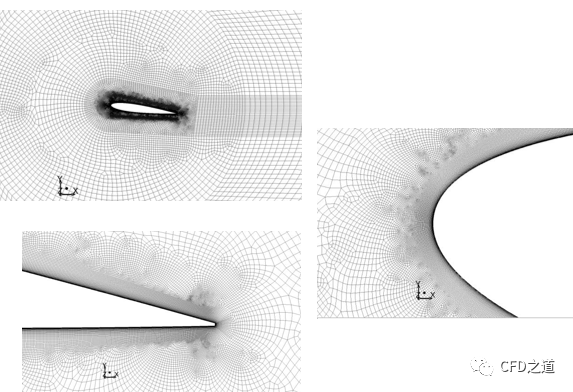
下图显示了前缘 (a) 和后缘 (b) 附近的湍流结构。在前缘附近，可以清楚地看到层流-湍流转捩，其是由层流分离气泡触发的。在后缘附近，湍流结构已经相对较大，但在展向方向上仍然显得不同步(没有轴向在展向方向上的大尺度二维结构)。

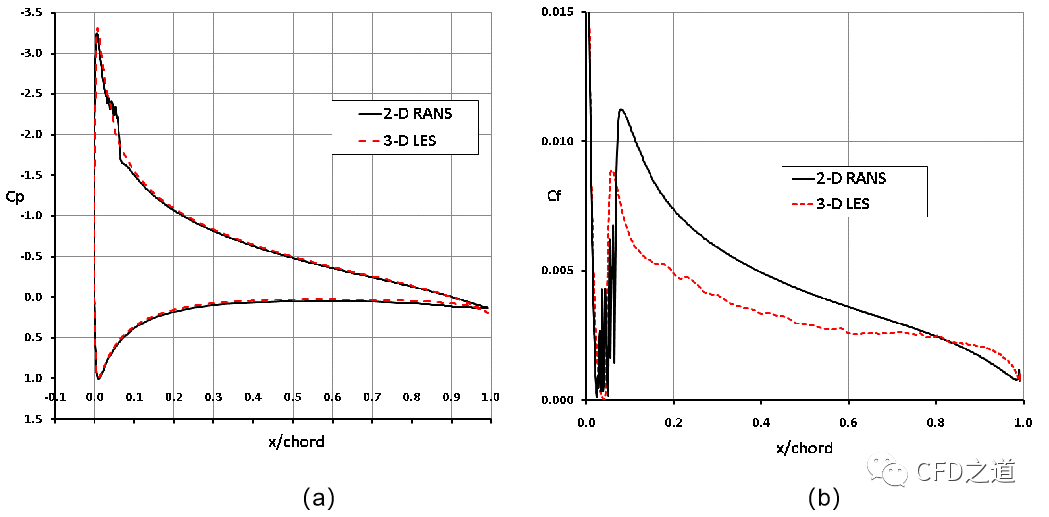
在开始平均化过程之前，大约模拟了1e4个时间步。下图(a)显示了翼型吸力侧的壁面压力系数Cp和图(b)壁面剪切应力系数Cf与使用SST模型的RANS计算(Menter，1994)的比较。这里不打算详细讨论模拟过程，但将壁面剪且应力与校准好的RANS模型进行比较表明，网格的分辨率仍然不足以捕捉近壁面细节。因此在前缘区与SST模型相比，壁面剪应力被明显低估了约30%。随着尾缘的接近，对比效果改善，这主要是因为边界层厚度增加，而壁面剪且应力减小，这意味着大涡模拟获得了更高的相对分辨率。基于此模拟，估计需要在流向和展向两个方向上将网格细化2倍，才能再现正确的壁面剪应力。虽然这样的分辨率并不超出现有计算机的能力范围，但对于日常模拟来说，它的计算开销仍然太高了。

总体而言，在可预见的将来，工业流动的LES将被限制在对不涉及壁面边界层的流动模拟上，或在强烈减少的几何形状中的壁面边界流动，优先在低Re数下。传统LES方法的局限性是混合RANS-LES模型发展的驱动力。