SRS模型｜03 常用的SRS模型

本文描述常见的SRS模型。

3.1 SAS模拟方法

本文描述尺度自适应模拟（Scale-Adaptive Simulation，SAS）的基本介绍。

原则上，所有的RANS模型都可以在非稳态模式(URANS)下求解。然而，经验表明，经典的URANS模式不能提供任何湍流谱内容，即便是网格和时间步长的分辨率足以满足这一目的也不行。长期以来，人们一直争辩说这种行为是RANS平均化过程(通常是时间平均化)所导致的自然结果，RANS平均化过程从速度场中消除了所有与湍流相关的内容。通过这一观点，我们得出结论：URANS只有在“尺度分离”的情况下才能工作。例如，解决频率比湍流低得多的时间变化。一个例子是绕过缓慢振荡翼型的流动，其中湍流完全由RANS模型模拟，并且仅在时间上解决了缓慢的叠加运动。这种情况的一个临界情况是流过钝体，就像横流中的圆柱体。对于这样的流动，即使没有独立的外力，URANS 模拟也提供了不稳定的介绍结果。产生的涡旋脱落频率不一定比最大湍流尺度的频率低很多。下图描述了这种情况。它表明，即使在如 Re=1e6 的相对较高雷诺数时，URANS 模型（在这种情况下为 SST）也会产生单模涡旋脱落。涡一直延伸到圆柱尾迹中，并且保持单一频率。这与宽带湍流谱的实验观测结果相矛盾。

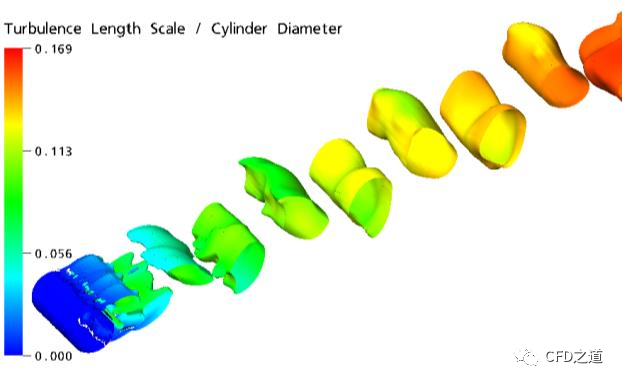
然而，如一些出版物(如Menter和Egorov ，2010，Egorov等，2010)所示，可以基于可追溯到Rotta(见Rotta，1972)的理论概念推导出一类RANS模型，其性能类似于定常流动中的标准RANS模型，但允许为某些类型的非定常流动形成宽带湍流谱。这种模型被称为尺度自适应仿真(Scale-Adaptive Simulation，SAS)模型。下图说明了这种情况，该图显示了与上图相同的模拟参数，但使用的是 SAS-SST 模型。因此，上图中看到的行为并非所有 RANS 模型都固有，而仅适用于以特殊方式派生的模型。

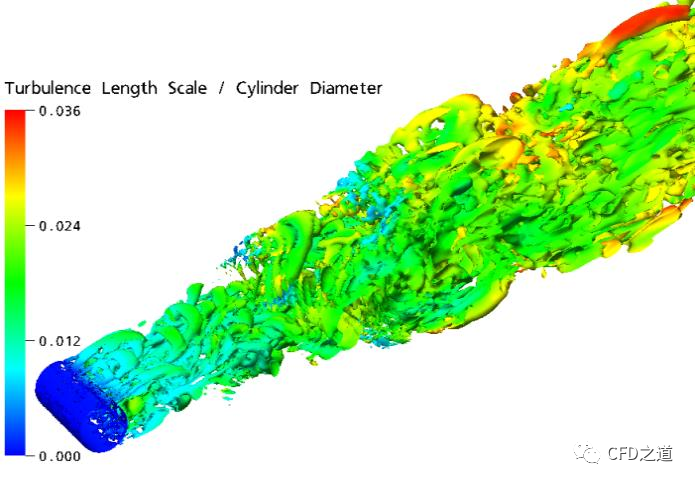
SAS模型的概念在引用的参考文献中有非常详细的描述，在此不再重复。然而需要提供基本的模型公式来讨论模型的特性。标准RAN和SAS模型之间的区别在于对尺度定义方程(通常是、或方程)的处理上。在经典的RANS模型中，尺度方程是基于与k方程的类比，使用简单的量纲分析来建模的。SAS模型的尺度方程是基于Rotta提出的湍流长度尺度的精确输运方程，该方法2010年被Menter和Egorov重新修正，避免了原始Rotta模型的一些局限性。结果表明，速度场的二阶导数需要包含在尺度方程的源项中。最初的SAS模型(Menter和Egorov 2010)被表示为两方程模型，其中变量用于尺度方程：

主要的新项是包括von Karman长度尺度 的项，该项没有出现在任何标准的RANS模型中。二阶速度导数允许模型将其长度尺度调整为那些已在流动中解析的结构。此功能在标准RANS模型中不存在。这导致了上图中所示的行为，与此类流动的实验观测结果更接近。

可以将项转换并实现为任何其他尺度定义方程，从而获得SAS功能，就像SAS-SST模型的情况一样。对于SAS-SST模型，变换后的w方程中的附加项被设计为对SST模型的边界层RANS性能没有(或至少是最小)影响，但可以对自由剪切流产生适度的影响(Davidson，2006)。

对于有壁面边界的流动，SAS模型将保持稳态的RANS模式，而在具有大而不稳定的分离区的流动中，SAS模型可以切换到SRS模式。

3.2 分离涡模拟方法

分离涡流模拟(Detached Eddy Simulation，DES)由Spalart和他的同事(Spalart，1997,2000，Travin，2000，Stletts，2001)提出的，通过构造一种基于所提供的网格分辨率在RAN和LES之间切换的混合格式来消除LES模型的主要局限性。通过这种形式，RANS模型完全覆盖了壁面边界层，而远离壁面的自由剪切流则采用LES模式计算。该格式在数学上相对简单，可以建立在任何RANS湍流模型之上。DES在湍流领域获得了极大的关注，因为它是第一个允许将SRS功能包含到常见工程流动模拟中的SRS模型。

在DES模型中，RAN和LES之间的切换基于如下标准：

式中，为局部计算网格的最大长度；双方程模型（k-epsilon、k-omega模型）的实际表达式为：

当网格尺寸细化到极限值时i，DES限制器被激活，并将模型从RANS模式切换到LES模式。对于壁面边界层，只要满足条件即可保持RANS模型，其中为边界层厚度。

DES模型的目的是在附着流动区域以RANS模型运行，在远离壁面的分离区域切换到LES模式。这表明，原始DES公式及其后续版本在切换到网格间距作为定义长度尺度后，要求网格和时间步长分辨率达到LES的要求。一旦限制器被激活，模型就会失去RANS校准，所有相关的湍流信息都需要求解。由于这个原因，在自由剪切流中，DES方法并没有提供比标准LES模型更少的计算成本。然而DES允许用户避免在LES模式下覆盖壁面边界层所带来的高计算成本。

同样重要的是，DES限制器可以通过再附边界层内的网格细化来激活。然而这是不可取的，因为它通过降低涡流粘性来影响RANS模型，从而导致网格诱导分离(GIS)，正如Menter和Kuntz(2002)所讨论的那样，边界层可以根据网格间距在任意位置分离。为了避免这种限制，遵循 Menter 和 Kuntz (2003) 的“屏蔽”边界层免受 DES 限制器的建议，Spalart等人(2006)将DES概念扩展到Delayed DES(DDES)。 DDES 扩展也可以应用于 DES-SA 公式，产生 DDES-SA 模型；以及应用于 SST 模型，产生 DDES-SST 模型。

因此，对于双方程模型，k方程中的耗散项被重新表示为：

函数的设计方式是在壁面边界层内给出，在远离壁面的地方给出。这个函数的定义很复杂，因为其涉及到当流动从壁面分离时，在适当的屏蔽和不抑制已解析湍流的形成之间取得平衡。当函数混合到边界层边缘附近的LES中时，不可能实现完美的屏蔽。DDES的极限通常在的范围内，因此允许比DES小5倍的网格，而不会对RANS覆盖的边界层产生负面影响。然而，即使经常达到这个限制，即便使用DDE也可能出现GIS。

ANSYS CFD 中有许多 DDES 模型可用，这些模型在 RANS 和 LES 之间的切换方面遵循相同的基本思想，它们的不同之处主要在于RANS 功能，应相应地进行选择。

本文描述分离涡模拟（Detached Eddy Simulation，DES）的基本情况。

3.3 SDES模拟

屏蔽分离涡模拟（Shielded Detached Eddy Simulation，SDES）是DDES模型家族的成员，但为屏蔽函数和网格尺度的定义提供了替代方案。其对湍流模型的影响一如既往地表示为k方程中的附加汇项：

屏蔽函数能比比上述相应的函数提供更强的屏蔽。因此，可以减少基于网格长度定义的模型自然屏蔽。SDES模型中使用的网格长度尺度定义为：

第一部分为传统的LES网格长度尺度定义，第二部分基于DES中的最大网格长度。但是，因子0.2可确保对于高度拉伸的网格，网格长度尺度比DES/DDES小5倍。在LES模式中，由于网格长度尺度以二次形式进入涡旋粘性的定义中，这意味着在这种情况下减小了25倍。结果表明，这极大地减少了经常观察到的DES/DDES模型从RAN到LES‘过渡’缓慢的问题。需要注意的是，这种更具侵略性的长度尺度与传统DDES屏蔽功能的组合将严重降低DDES的屏蔽特性，因此不推荐使用。

SDES模型常数也与DES/DDES模型不同，DES/DDES模型是基于衰减各向同性湍流(Decaying Isotropic Turbulence，DIT)进行校准的，目的是使湍流谱与特定运行时间后的数据相匹配。然而在工程流动中，人们通常必须处理剪切流动，而剪切流动应该使用减小的Smagorinky常数。这可以通过设置来实现。网格长度尺度的重新定义和修正后的常数相结合，使得在拉伸网格上分离剪切流时的涡粘性减小了约60倍，这将导致从RANS到LES的过渡更快。

屏蔽函数的公式化使得其能够在任何网格上提供基本上渐近的屏蔽。。在平板试验中，该极限值被推到以下。

下面的测试案例显示了SDES/SBES模型相对于DDES改进的屏蔽性能。案例展示的是轴对称几何结构中的扩散流动，具有小的分离气泡。由于逆压梯度的存在，边界层增长很快，而的大幅增加导致很难实现屏蔽。

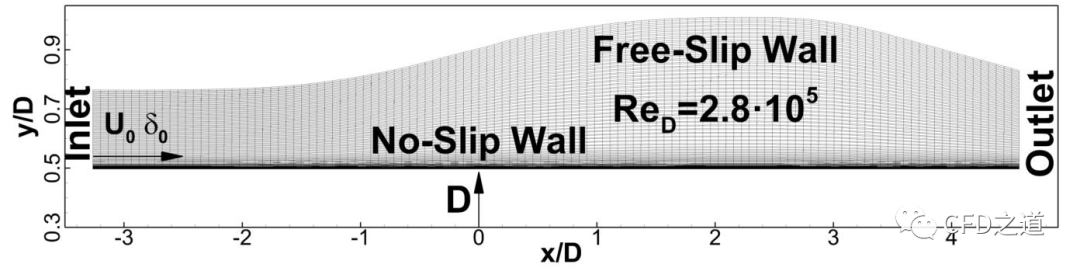
计算区域如上图所示。区域沿流动方向的长度约为7.8·D(D是圆柱体的直径，x/D=0对应于实验中的分离点)。对于此流动，使用标准RANS网格，沿流向和圆周方向的步长分别为和(圆周方向的网格步长因轴对称几何形状而沿径向变化)。这里是入口截面的边界层厚度。壁面网格的高度被选择为在整个区域内满足条件，并且边界层内大约有30层网格。

从下图所示的SBES和DDES混合函数的轮廓可以看出，SBES覆盖了整个边界层，包括由于分离气泡而导致的边界层的快速增长区域，而DDES只保留了入口处的区域部分。这意味着在你呀压力梯度条件下，DDE的屏蔽性能实质上受到损害。

下图所示的涡粘度场也有类似的观测结果。SBES的涡粘度水平与SST模型(未显示)相当，而DDES模型在逆压梯度区产生的涡粘度水平要低得多。

3.4 SBES模型

SBES模型的概念建立在SDES公式的基础上。在SDES模型之外，SBES还使用屏蔽函数在RANS和LES下的不同湍流模型之间进行显式切换。一般而言，这意味着湍流应力张量：

式中，为应力张量的RANS部分，为应力张量的LES。在两个模型部分都基于涡粘性概念的情况下，公式简化为

如果没有强屏蔽，这样的公式是不可行的。当使用来自 DDES 模型的常规屏蔽函数时，相应的模型将无法在任何网格上保持零压力梯度 RANS 边界层。

相对于其他全局混合RANS/LES模型，目前推荐使用SBES模型。它具有以下优势：

• RANS边界层的渐近屏蔽
• 在LES区域中显式切换到用户指定的LES模型
• 从RAN到LES区域的快速“过渡”
• 基于屏蔽函数的RANS和LES区域清晰可视化
• 一次在LES/WMLES模式下的壁面型LES功能

3.5 大涡模拟

不同LES模型的详细信息可以在相应求解器的用户文档和理论文档中找到。如前文所述，大涡模拟的主要目的是为最小的(未解析的)尺度涡提供足够的阻尼。出于这个原因，不建议使用复杂的公式，而是停留在简单的代数模型上。使用最广泛的LES模型是Smagorinsky(1963)模型：

Smagorinsky模型的主要缺点是对于层流剪切流，它的涡粘性不为零()，为此，该模型还要求在粘性子层中设置近壁面阻尼函数。对于简单的层流剪切流，需要一个能够自动提供零涡粘性的LES公式。这在计算层流-湍流转捩流动时尤为重要，因为Smagorinsky模型会对层流产生负面影响。

提供此功能的最简单模型是Nicoud和Ducros（1999）的壁适应局部涡流粘度模型（Wall-Adapting Local Eddy Viscosity，WALE）。Dynamics LES模型也可以实现同样的效果，但代价是复杂度稍高。经典的大涡模拟都没有解决工业上的主要问题，即在中到高雷诺数时，壁面有界流动的计算成本过高。

然而，在雷诺数非常低的情况下，LES可以作为一种工业选择。在这种条件下，壁面边界层内可能是层流，湍流值在分离剪切层和分离的流动区域中存在。这种情况可以通过分析给定流定的RANS涡粘解来确定。在边界层内湍流粘度与分子粘度之比小于的情况下，可以假设边界层为层流，不需要解析近壁面湍流。在低雷诺数的阀门或其他小规模设备周围的流动中，可以观察到这种现象。

大涡模拟也可以应用于自由剪切流，与壁面有界流动相比，这种流动对分辨率的要求要低得多。

3.6 WMLES模型

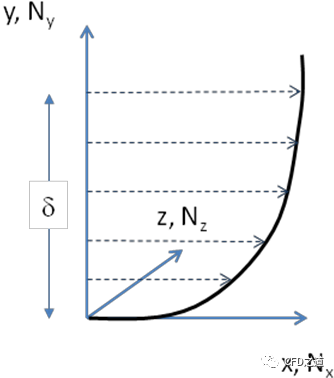
壁面模拟LES(Wall Modeled LES，WMLES)是经典LES的替代方法，其降低了传统壁面解析LES的严格且依赖于Re数的网格分辨率要求。WMLE模型的基本思想如下图所示。如前文所述，近壁湍流长度尺度随与壁面距离线性增加，从而在接近壁面时产生越来越小的涡流。这种影响受到分子粘度的限制，分子粘度会抑制粘性子层内的涡。随着Re数的增加，粘性子层变薄，涡旋变得越来越小。为了避免这些小的近壁面尺度的分辨率，可以将RANS和LES模式合起来，使RANS模式覆盖近壁层，然后在网格间距变得足以分辨局部尺度时切换到LES公式。这在图中可以看到，其中RANS层延伸到粘性子层之外，从而避免了解析图中描绘的内部“第二”行涡。

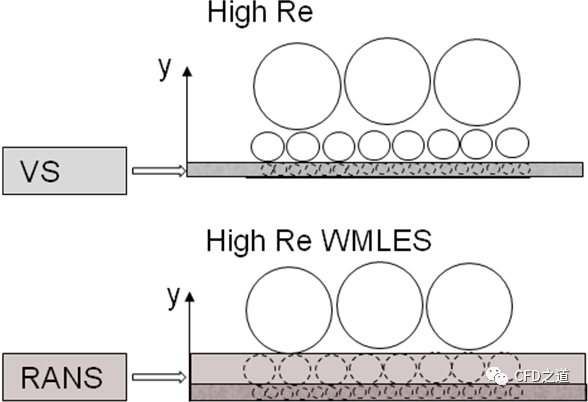
ANSYS CFD中的WMLES公式是基于Shur等人(2008)的公式：

式中，为壁距，为冯·卡门常数，为应变率，为近壁阻尼函数。该公式是为了适应ANSYS通用CFD程序的需要而提出的。在壁面附近，min函数选择Prandtl混合长度模型，而在远离壁面位置切换到Smagorinsky模型。

对于壁面边界层流动，WMLES的分辨率要求取决于模型公式的细节。在ANSYS Fluent和ANSYS CFX中，它们是(假设此估计的x为流向，y为墙法线，z为展向方向，如下图所示)：

式中，Nx、Ny和Nz分别是每个边界层厚度在流向、壁面法线和展向方向上的网格单元数量。换句话说，覆盖一个边界层体积需要大约6000-8000个网格单元，这也是低雷诺数下经典LES模型的最小分辨率。实际上，在低雷诺数条件下，WMLES基本上变成了经典的LES。WMLES的优点是相对于边界层厚度的分辨率要求与雷诺数无关。

3.7 Embeded/Zonal LES

ELES背后的思想是在预处理阶段用不同的湍流处理预定义不同的区域。在模拟之前，计算区域被分成RANS和LES部分。在不同区域之间，湍流模型从RANS切换到LES/WMLES。为了保持一致性，通常在RANS-LES界面处引入合成湍流。ELES实际上并不是一种新模型，而是一种以分区方式结合现有技术要素的模型组合。因此，每个区域的建议与适用于单个模型的建议相同。

在ANSYS Fluent中可以使用Embedded LES（Cokljat等，2009），该模型允许将大多数RANS模型与预定义RANS和LES区域中的所有非动态LES模型分别组合。使用涡方法（Vortex Method）在RANS-LES界面上实现了从模拟湍流到解析湍流的转换（Mathey等，2003）。

在CFX中，使用一种称为分区强制LES模型(Zonal Forced LES，ZFLES)的方法可以实现类似的功能(Menter等，2009年)。该模拟基于预先选择的RANS模型，在由CEL表达式指定的LES区域中，动量方程和湍流方程中的强制项被激活。这些项将RANS模型推向WMLES模型。此外，在RANS-LES界面处还会产生合成湍流。

ANSYS Fluent中还有一个附加选项，涉及使用全局湍流模型（SAS、DDES、SDES、SBES），并在预定义界面激活合成湍流的生成。代码负责通过界面平衡已解析和已模拟的湍流。该选项可用于在自然流非稳定性不足的情况下强制全局混合模型进入非稳定状态。与在不同区域使用不同的模型的ELES不同，该模型在界面的上游和下游使用相同的湍流模型。

这种强迫也可以通过在ANSYS CFX中指定一个薄的LES区域并在全局使用SAS或DDES/SDES/SBES模式来实现。SBES模型最适合此场景。

3.8 非定常入口/界面湍流

经典LES要求在湍流入口/界面（RANS-LES界面）向LES区域提供非定常脉动。这使得LES比通常指定平均湍流量（k和e，或k和w）的分布的RANS的要求更高。一个例子是完全紊流的通道（管道）流，流体在入口以完全紊流状态进入区域，用户需要通过非定常的入口速度分布在这样的入口位置提供合适的解析湍流。入口分布的组成方式必须使其时间平均值与正确的平均流动入口分布以及所有相关湍流特性(湍流时间和长度尺度、湍流应力等)相对应。对于完全湍流的槽道和管流，可以通过在流动方向上应用周期性边界条件来规避这一要求。因此，流动由沿流向作用的动量方程中的源项驱动。通过这种“技巧”，在出口处离开该区域的湍流在进口处再次进入该区域，从而避免了需要明确指定非定常湍流分布。这种方法显然只能用于非常简单的问题中，其要求在流向上有足够长的区域，以允许在区域内形成独立于周期边界的湍流结构。

在大多数实际情况下，几何不允许完全周期性的模拟。然而，它可以在入口处具有完全发展的分布（同样通常是管道/通道流）。在这种情况下，可以在单独的周期性区域上执行周期性前置模拟，然后将在该模拟的任何横截面获得的非定常分布插入复杂 CFD 区域的入口。这种方法需要直接耦合两个单独的 CFD 模拟，或存储来自周期性模拟的足够数量的非定常分布以供完整模拟读入。

然而，在实际情况下，入口分布可能不会完全发展，并且没有简单的方法来产生一致的入口湍流。在这种情况下，可以根据RANS给定的入口分布生成合成湍流。这些通常是从LES入口上游的区域的前置RANS计算获得的。

目前有很多产生合成湍流的方法。在 ANSYS Fluent 中，使用最广泛的方法是涡旋法 (Vortex Method，VM)（Mathey 等，2003 年），该方法在入口处生成了大量离散的旋涡，通过对这些旋涡的分布、强度、尺寸进行模拟，以提供真是湍流的理想特性。 VM 的输入参数是来自上游 RANS 计算的两个尺度（k 和 e，或 k 和 w）。 CFX 使用通过合适的谐波函数产生合成湍流作为 VM 方法的替代方案（如 Menter 等，2009）。

壁面有界流动中高质量合成湍流的特点是在入口下游迅速恢复时间平均湍流应力张量。这可以通过绘制敏感量（如时间平均壁面剪切应力或传热系数）并观察其在入口下游的变化来检查。此外，还建议使用Q标准的等值面（）（S-应变率，-涡度）来直观地研究湍流结构。即使在模拟中经过几百个时间步，也可以完成此操作。

由于合成湍流不可能在所有方面都与真实湍流重合，因此应避免将入口/界面设置在具有强烈非平衡湍流活动的为准。在边界层流动中，这意味着入口或RANS-LES界面应该位于任何强非平衡区(例如分离区)上游若干层(至少~3-5)厚的边界层处。入口/界面下游的边界层需要以足够高的空间分辨率进行解析。

本文译自《Best Practice: Scale-Resolving Simulations in ANSYS CFD》
原文作者：F.R. Menter

”