一维热传导方程为：

式中，为场变量；为时间；为介质扩散率。

前面的课程中使用的FTCS格式中，对时间项采用的向前差分格式只有一阶精度，我们可以想办法构造更高精度的时间格式，如本文后面将要使用的Runge-Kutta方法。

1 离散方程

Runge-Kutta法试图在时间点与之间应用更多的中间点计算来提高时间项离散精度。这里采用文献[16]所提供的一种三阶精度的Runge-Kutta格式来离散传热方程的时间项。对于空间项依然使用二阶中心差分格式。这种Runge-Kutta离散方法的离散误差为。

三阶Runge-Kutta格式对传热方程时间项进行离散后得到的方程为：

2 程序代码

可以编写程序代码：

using Printf
# -------------------基础测试数据------------------------#
# x_l与x_r分别为计算域坐标
# dx,dt分别为空间网格尺寸与时间步长
# t为最终时刻
x_l = -1.0
x_r = 1.0
dx = 0.025
dt = 0.001
t = 1.0
 
# nx与nt分别为网格数量与时间步数
nx = Int64((x_r - x_l) / dx)
nt = Int64(t / dt)
 
# alpha为物性参数
alpha = 1 / (pi * pi)
 
u = Array{Float64}(undef, nx + 1, nt + 1)
x = Array{Float64}(undef, nx + 1)
u_e = Array{Float64}(undef, nx + 1)
u_error = Array{Float64}(undef, nx + 1)
 
for i = 1:nx+1
    x[i] = x_l + dx * (i - 1)  # 得到网格点的x坐标
    u_e[i] = -exp(-t) * sin(pi * x[i]) # 得到理论值用于后面比较
end
# --------------------------------------------------------------#
 
# 利用中心差分计算方程的右侧项
# r = α ∂2u/∂x2
function rhs(nx, dx, u, r, alpha)
    for i = 2:nx
        r[i] = alpha * (u[i+1] - 2 * u[i] + u[i-1]) / (dx * dx)
    end
end 
 
# 三阶龙格库塔法时间离散
function numerical(nx, nt, dx, dt, x, u, alpha)
    un = Array{Float64}(undef, nx + 1) # 存储每个时间步的数值解
    ut = Array{Float64}(undef, nx + 1) # 存储RK积分的临时数组
    r = Array{Float64}(undef, nx)
 
    k = 1 
    for i = 1:nx+1
        un[i] = -sin(pi * x[i])
        u[i, k] = un[i]
    end
 
    # 边界条件
    un[1] = 0.0
    un[nx+1] = 0.0
    ut[1] = 0.0
    ut[nx+1] = 0.0
 
    for j = 2:nt+1
        rhs(nx, dx, un, r, alpha) 
        for i = 2:nx
            ut[i] = un[i] + dt * r[i]
        end
 
        rhs(nx, dx, un, r, alpha)
        for i = 2:nx
            ut[i] = 0.75 * un[i] + 0.25 * ut[i] + 0.25 * dt * r[i]
        end
 
        rhs(nx, dx, un, r, alpha)
        for i = 2:nx
            un[i] = (1.0 / 3.0) * un[i] + (2.0 / 3.0) * ut[i] + (2.0 / 3.0) * dt * r[i]
        end
 
        k = k + 1
        u[:, k] = un[:]
    end
end
 
# -----------------------------------------------------------#
 
numerical(nx, nt, dx, dt, x, u, alpha)
u_error = u[:, nt+1] - u_e
 
# 将数据写入到文件中
field_final = open("field_final1.csv", "w");
write(field_final, "x", " ", "ue", " ", "un", " ", "uerror", " n")
 
for i = 1:nx+1
    write(field_final, @sprintf("%.16f", x[i]), " ", @sprintf("%.16f", u_e[i]), " ",
        @sprintf("%.16f", u[i, nt+1]), " ", @sprintf("%.16f", u_error[i]), " n")
end
 
close(field_final)

计算结果及离散误差如下图所示。

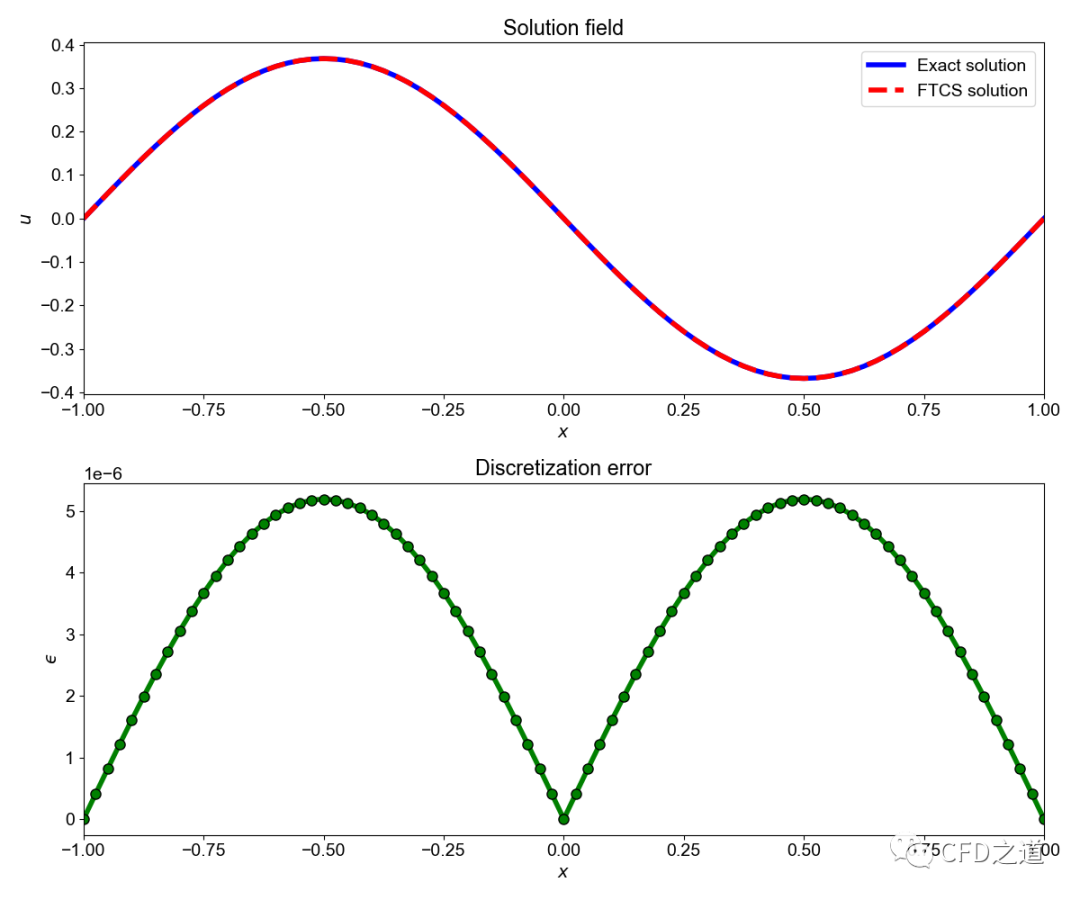
3 尝试

对程序代码进行以下修改并观察计算结果：

• 网格尺寸不变，将时间步长dt成倍增大
• 时间步长不变，将网格尺寸dx成倍增大或减小
• 组合时间步长及网格尺寸

这里所使用的三阶Runge-Kutta方法依然是一种显式算法，因此在计算过程中时间步长不能太大，若想要使用大的时间步长，只能通过增大网格尺寸来维持计算稳定。

4 参考文献

[16] Gottlieb, S.; Shu, C.W. Total variation diminishing Runge-Kutta schemes. Math. Comput. Am. Math. Soc.1998, 67, 73–85.