一维热传导方程为：

式中，为场变量；为时间；为介质扩散率。传热方程描述了介质中场变量温度随时间的演化。

热传导方程的离散有多种方法，如有限体积法[11]、有限差分法[12]、有限元法[13]、谱方法[14]等。本文研究的是对所有偏微分方程(PDE)进行离散的有限差分方法，此方法方法相对简单，在学习CFD的初期就很容易理解。有限差分法将线性或非线性偏微分方程转化为一组线性或非线性常微分方程(ODE)，这些常微分方程可以用矩阵代数技术来求解。

在推导热方程的有限差分格式之前，在平面上定义网格点。设和分别为空间和时间方向上的网格间距，如下图所示，对于任意整数和，有。这里使用符号表示。

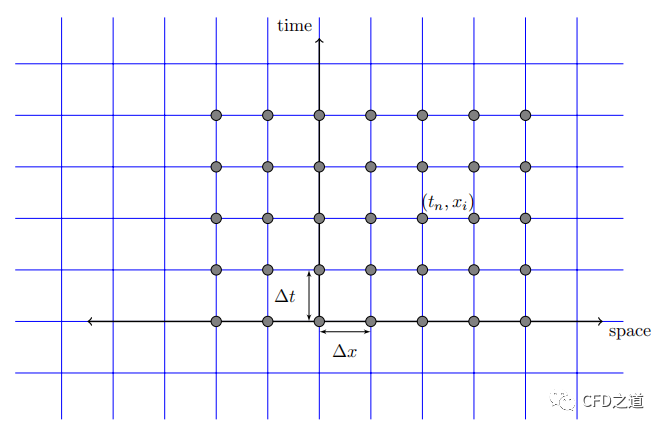
有限差分法利用泰勒级数展开得到偏微分方程组的离散近似。

函数关于点的泰勒级数展开式由下式给出：

式中表示n的阶乘，为截断项，给出了阶泰勒级数展开式与原函数之间的差别。将原微分方程的精确解与有限差分近似解之差称为离散误差或截断误差。离散误差中的先导项决定了有限差分格式的精度。任何偏微分方程的有限差分格式都必须具有两个性质：一致性和稳定性，才能保证收敛。这里推荐一本教科书Finite difference schemes and partial differential equations”[15]，其详细地解释了有限差分格式的数值行为。本文主要研究有限差分法在计算流体力学中的应用。

下文分别使用FTCS、Runge-Kutta、Crank-Nicolson、ICP格式对方程进行离散求解，并将数值解与解析解进行比较。方程(1)的解析解为：

同时计算绝对误差：

1 离散格式推导

推导离散热方程的时间向前空间中心(Forward Time Central Space, FTCS)数值格式。利用离散域的泰勒级数时间展开式，可以得到：

方程(4)为传热方程时间项的一阶精度表达式。为了获得传热方程二阶项的有限差分表达式，可以使用泰勒级数展开：

式(5)与式(6)相加得到二阶偏微分项的表达式：

舍弃高阶无穷小项，并将式(7)其代入式(1)，可以得到：

重新排布各项，可写成显式格式：

上述格式记为格式，此离散格式在时间上是一阶精度，在空间上是二阶精度。可以使用较多的网格点来获得高阶公式，以获得更好的近似值。如果给出了热传导方程的初始解，那么就可以使用式(9)进行求解。

可以从式(9)中观察到，下一个时间步长的解仅取决于前一个时间步长的解。这些数值格式被称为显式数值格式，它们很容易编写程序代码。然而显式格式受到一些稳定性准则的限制，这些稳定性准则限制了可以在空间和时间方向上使用的最大步长，因此显式格式的计算量很大。

2 程序分析及代码

测试算例：

• 计算区域
• 物性参数
• 初始边界条件：
• 空间网格尺寸，时间步长

首先初始化数组，并利用初始条件对数组中的所有元素赋值。

使用式(9)计算得到一个时间步长后的计算结果，将该求解结果存储在矩阵的第一列中，该矩阵维度为，其中是计算区域的空间分割数量，是初始时间和最终时间之间的时间步数。

写成计算程序如下。

using Printf
 
# x_l与x_r分别为计算域坐标
# dx,dt分别为空间网格尺寸与时间步长
# t为最终时刻
x_l = -1.0
x_r = 1.0
dx = 0.025
dt = 0.001
t = 1.0
 
# nx与nt分别为网格数量与时间步数
nx = Int64((x_r - x_l) / dx)
nt = Int64(t / dt)
 
# alpha为物性参数
alpha = 1 / (pi * pi)
 
# 定义一些数组用于存储结果数据
x = Array{Float64}(undef, nx + 1)    # 存储某一时间点上的数值解
u_e = Array{Float64}(undef, nx + 1)  # 存储解析解
un = Array{Float64}(undef, nt + 1, nx + 1) # 存储所有时间点数据
u_error = Array{Float64}(undef, nx + 1) # 存储每个节点上的误差
 
# 初始化
for i = 1:nx+1
    x[i] = x_l + dx * (i - 1) # 得到网格节点的x坐标
    un[1, i] = -sin(pi * x[i]) # 初始化边界节点值
    u_e[i] = -exp(-t) * sin(pi * x[i]) # 解析解t=1.0
end
 
beta = alpha * dt / (dx * dx)
 
# 时间推进,得到最终时刻各节点上的值
for k = 2:nt+1
    for i = 2:nx
        un[k, i] = un[k-1, i] + beta * (un[k-1, i+1] - 2 * un[k-1, i] + un[k-1, i-1])
    end
    un[k, 1] = 0.0  # 边界值x=-1
    un[k, nx+1] = 0.0 # 边界值x=1
end
 
u_error = un[nt+1, :] - u_e
 
# 将数据写入到文件中
field_final = open("field_final.csv", "w")
write(field_final, "x", " ", "ue", " ", "un", " ", "uerror", "n") #写入表头
 
# 循环写入最终时刻各节点上的值到文件中
for i = 1:nx+1
    write(field_final, @sprintf("%.16f", x[i]), " ", @sprintf("%.16f", u_e[i]), " ",
        @sprintf("%.16f", un[nt+1, i]), " ", @sprintf("%.16f", u_error[i]), "n")
end
close(field_final)

运行程序后生成CSV数据文件，其中保存最终时刻（1s时刻）的各节点值，如下图所示。

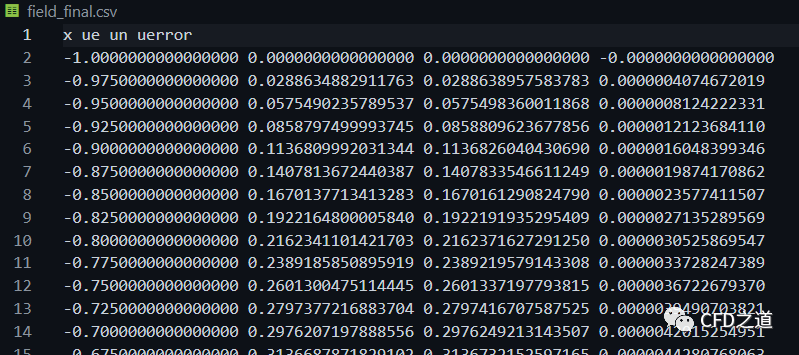
可以写个图形绘制程序将CSV中的数据读取并显示出来（这个代码留着后面还有用）。

# 注意在使用之前先安装包PyPlot、CSV及DataFrames
using PyPlot
using CSV
using DataFrames
 
# 设置图形字体及字号
rc("font", family = "Arial", size = 15.0)
 
# 读取文件
final_field = CSV.read("field_final.csv", DataFrame)
 
# 将数据转换为数字
x = convert(Array, final_field[:, 1])
u_e = convert(Array, final_field[:, 2])
u_n = convert(Array, final_field[:, 3])
u_error = convert(Array, final_field[:, 4])
 
# 以绝对值方式显示误差
for i = 1:Int64(length(u_error))
    u_error[i] = abs(u_error[i])
end
 
fig = figure("FTCS", figsize = (12, 8));
ax1 = fig[:add_subplot](2, 1, 1);
ax2 = fig[:add_subplot](2, 1, 2);
 
ax1.plot(x, u_e, lw = 4, ls = "-", color = "b", label = "Exact solution")
ax1.plot(x, u_n, lw = 4, ls = "--", color = "r", label = "FTCS solution")
ax1.set_xlabel("$x$")
ax1.set_ylabel("$u$")
ax1.set_title("Solution field")
ax1.set_xlim(-1, 1)
ax1.legend(fontsize = 14, loc = 0)
 
ax2.plot(x, u_error, marker = "o", markeredgecolor = "k",
    markersize = 8, color = "g", lw = 4)
ax2.set_xlabel("$x$")
ax2.set_ylabel("$ϵ$")
ax2.set_title("Discretization error")
ax2.set_xlim(-1, 1)
 
plt[:subplot](ax1);
plt[:subplot](ax2);
 
fig.tight_layout()
# fig.savefig("ftcs.pdf")
plt.show()

图形输出结果如下图所示：

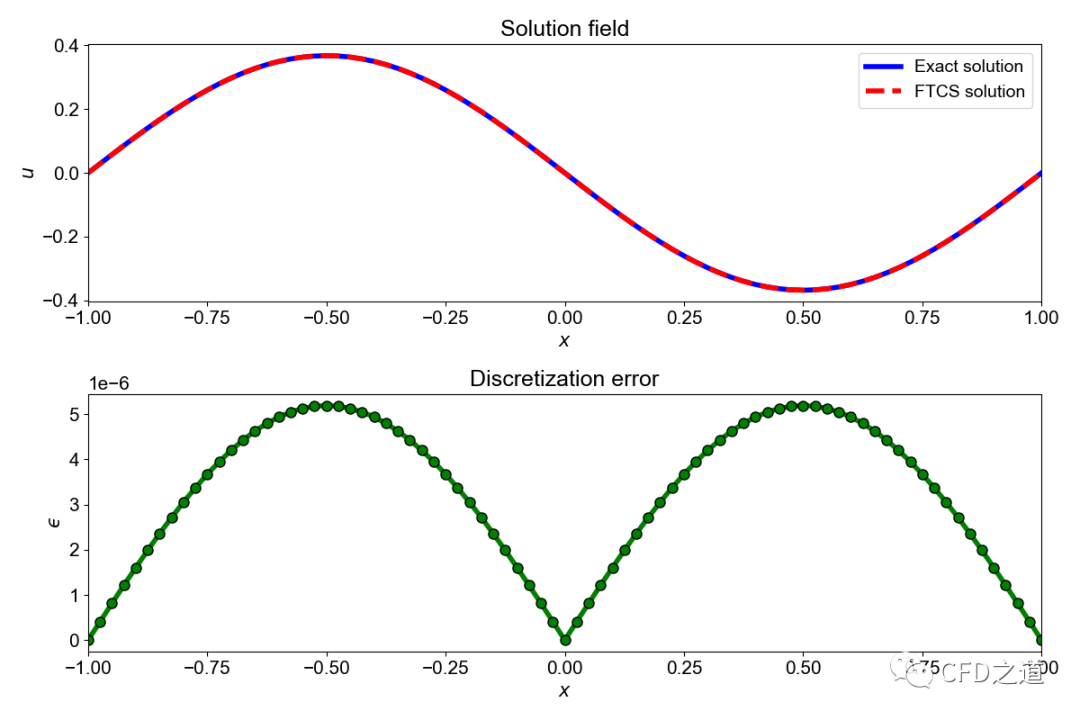
Julia的计算速度是真不错，但画图速度就不敢恭维了。

”

若想要查看物理量随时间变化，可以添加以下代码：

for i = 1:50:nt+1
    PyPlot.cla()
    plot(x,un[i,:],color="red",linewidth=2)
    PyPlot.title(@sprintf("times=%.3f s",i*dt))
    PyPlot.xlim(-1,1)
    PyPlot.ylim(-1,1)
    PyPlot.grid()
    PyPlot.pause(0.2)
end
PyPlot.show()

运行后如下如下图所示。时间足够长的话，结果会变成一条直线。

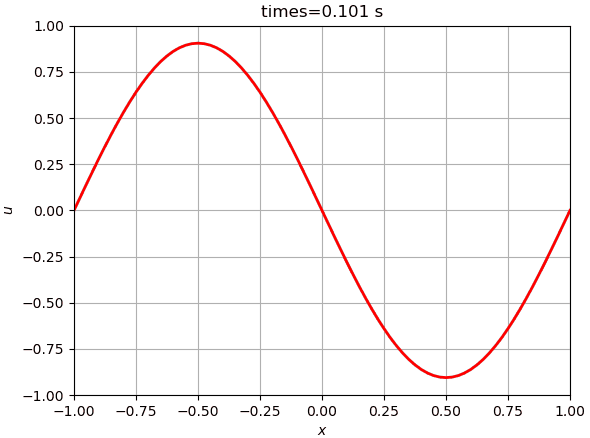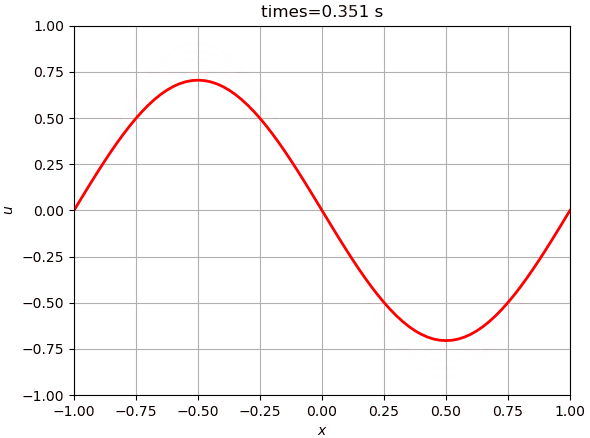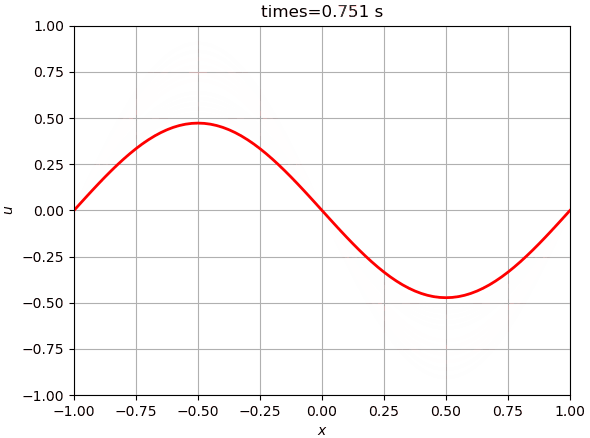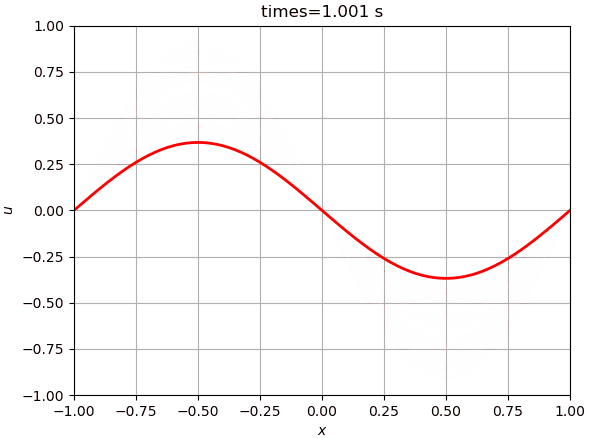
3 尝试

尝试对程序进行以下改变，观察计算结果：

• 修改时间步长dt，将其值放大10倍及缩小10倍
• 修改网格尺寸dx，将其值放大10倍及缩小10倍
• 组合以上因素进行计算
• 修改边界条件继续计算

显式计算对时间步长非常敏感，其要求较小的时间步长。网格尺寸对时间步长也有较大的影响，通常网格尺寸减小会要求更小的时间步长。

4 参考文献

[11] Versteeg, H.K.; Malalasekera, W. An Introduction to Computational Fluid Dynamics: The Finite Volume Method;Pearson Education: New York, NY, USA, 2007.

[12] Moin, P. Fundamentals of Engineering Numerical Analysis; Cambridge University Press: New York, NY, USA, 2010.

[13] Strang, G.; Fix, G.J. An analysis of the Finite Element Method; Prentice-Hall: Englewood Cliffs, NJ, USA, 1973;Volume 212.

[14] Canuto, C.; Hussaini, M.Y.; Quarteroni, A.; Thomas, A., Jr. Spectral Methods in Fluid Dynamics; Springer Science& Business Media: Berlin,Germany, 2012.

[15] Strikwerda, J.C. Finite Difference Schemes and Partial Differential Equations; Society for Industrial & Applied Mathmatics (SIAM): Philadelphia, PA, USA, 2004; Volume 88.