CFD Julia是一个编程模块,其包含了从一维传热方程到二维不可压缩Navier-Stokes流动问题的Julia程序设计。这是个利用Julia撸CFD的基础教程,适合作为计算流体力学课程的课后作业。
Julia是个不错的计算机程序设计语言,主要面向的是数据分析、数值计算之类强调计算性能的工作场合。官方介绍Julia兼具C语言的高性能及Python的高效率,是求解器开发界的潜力股语言。
1 基本介绍
CFD Julia的github仓库地址:https://github.com/surajp92/CFD_Julia。由于Julia最近几个版本更新变化较大,仓库中的很多代码需要经过一些调整才能运行。
更详细信息可参考:A Learning Module Structuring an Introductory Course on Computational Fluid Dynamics(https://www.mdpi.com/2311-5521/4/3/159)

涉及内容包括:
| Index | Description |
|---|---|
| 01 | 1D heat equation: Forward time central space (FTCS) scheme |
| 02 | 1D heat equation: Third-order Runge-Kutta (RK3) scheme |
| 03 | 1D heat equation: Crank-Nicolson (CN) scheme |
| 04 | 1D heat equation: Implicit compact Pade (ICP) scheme |
| 05 | 1D inviscid Burgers equation: WENO-5 with Dirichlet and periodic boundary condition |
| 06 | 1D inviscid Burgers equation: CRWENO-5 with Dirichlet and periodic boundary conditions |
| 07 | 1D inviscid Burgers equation: Flux-splitting approach with WENO-5 |
| 08 | 1D inviscid Burgers equation: Riemann solver approach with WENO-5 using Rusanov solver |
| 09 | 1D Euler equations: Roe solver, WENO-5, RK3 for time integration |
| 10 | 1D Euler equations: HLLC solver, WENO-5, RK3 for time integration |
| 11 | 1D Euler equations: Rusanov solver, WENO-5, RK3 for time integration |
| 12 | 2D Poisson equation: Finite difference fast Fourier transform (FFT) based direct solver |
| 13 | 2D Poisson equation: Spectral fast Fourier transform (FFT) based direct solver |
| 14 | 2D Poisson equation: Fast sine transform (FST) based direct solver for Dirichlet boundary |
| 15 | 2D Poisson equation: Gauss-Seidel iterative method |
| 16 | 2D Poisson equation: Conjugate gradient iterative method |
| 17 | 2D Poisson equation: V-cycle multigrid iterative method |
| 18 | 2D incompressible Navier-Stokes equations (cavity flow): Arakawa, FST, RK3 schemes |
| 19 | 2D incompressible Navier-Stokes equations (vortex merging): Arakawa, FFT, RK3 schemes |
| 20 | 2D incompressible Navier-Stokes equations (vortex merging): Hybrid RK3/CN approach |
| 21 | 2D incompressible Navier-Stokes equations (vortex merging): Pseudospectral solver, 3/2 dealiasing, Hybrid RK3/CN approach |
| 22 | 2D incompressible Navier-Stokes equations (vortex merging): Pseudospectral solver, 2/3 dealiasing, Hybrid RK3/CN approach |
2 练习环境搭建与配置
2.1 安装Julia
-
进入Julia官网https://julialang.org/,下载安装文件并进行安装
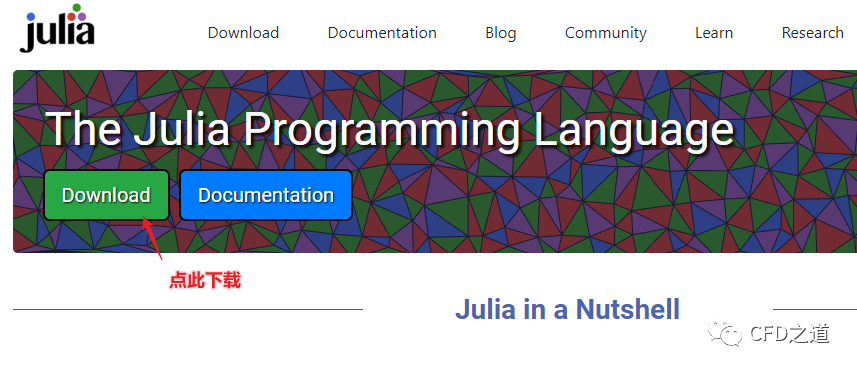
安装过程很简单,一路Next即可。
2.2 设置国内镜像源
Julia官方源下载速度奇慢,还有很多包在国内访问不到。国内热心网友做了镜像源,比较靠谱的镜像是北京外国语大学。之前浙大也有个镜像源,有一阵子访问不到,现在不知道什么情况。北外的源设置可以参考其官网https://mirrors.bfsu.edu.cn/help/julia/。
windows系统想要设置永久国内源可以这样做:
-
打开文件 C:用户(用户名).juliaconfigstartup.jl
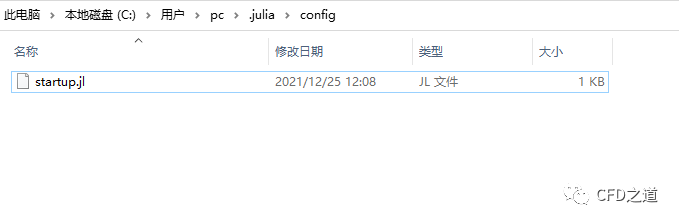
-
添加内容 ENV["JULIA_PKG_SERVER"] = "https://mirrors.bfsu.edu.cn/julia",如下图所示,保存文件即可
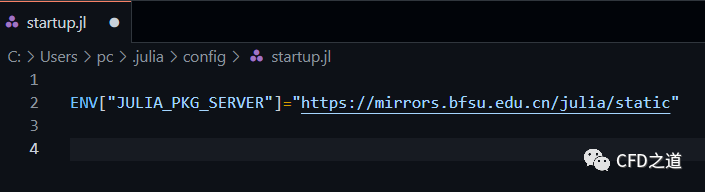
设置完毕后可以测试。
进入Julia环境,输入命令versioninfo(),若如下图所示则表示修改成功。
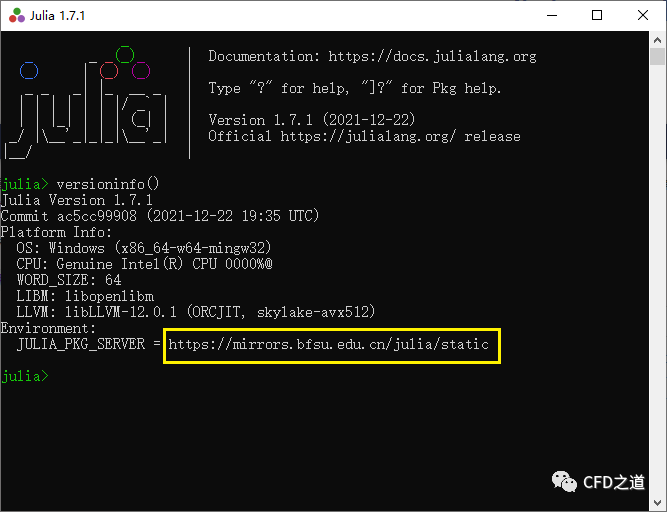
注:修改镜像源不是必须的,若本机访问外网速度可以的话,也可以不用修改镜像源。不过基于各方面原因,国内访问外网速度通常都超慢。
”
2.3 安装一些必要的包
Julia提供了一些基础程序设计功能,大量的特殊功能需要借助功能包来实现。这里以科学计算中最常见的绘图包PyPlot安装为例描述在Julia中程序包的安装过程。
-
启动Julia
-
依次输入以下命令
using Pkg
Pkg.add("PyPlot")
如下图所示。
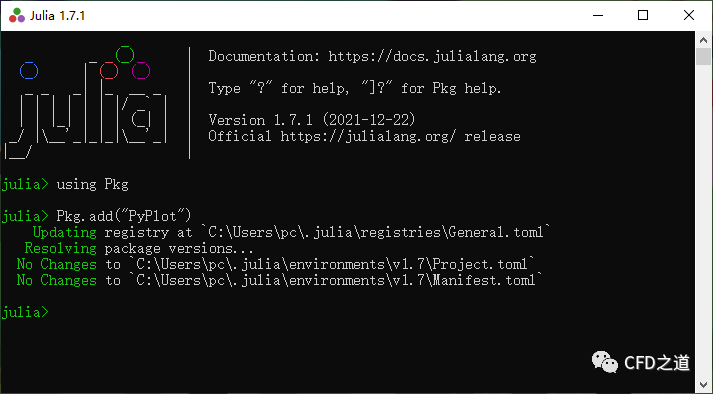
安装完毕后,输入命令Using PyPlot,如下图所示,若没有任何错误提示,则表示该包安装成功。
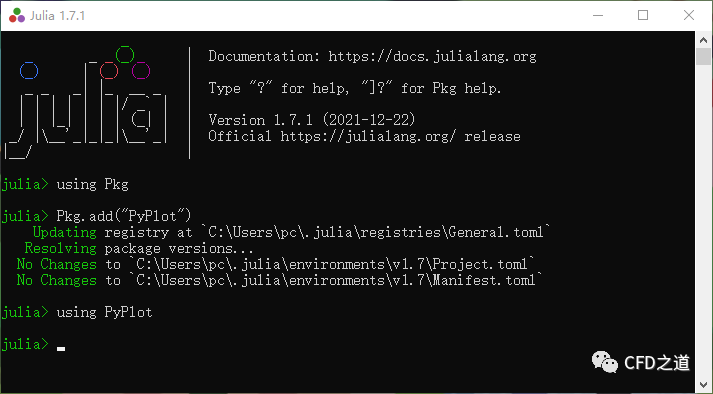
相同的方式可以使用命令Pkg.add("IJulia")安装IJulia包,该包可以与Jupyter配合使用,非常方便。
2.4 在vs code中使用Julia
julia官方提供了vs code插件。
-
搜索并安装插件Julia
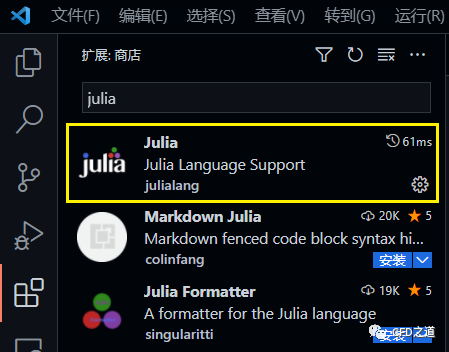
-
若想要在vscode中利用Jupyter编写Julia代码,还可以搜索并安装Jupyter
(本文结束)
本篇文章来源于微信公众号: CFD之道








评论前必须登录!
注册