将压力降-速度数据表拟合成以下的函数形式:
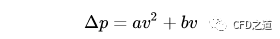
利用matlab或scipy只需要少数几行语句即可完成此类函数拟合。然而在微信小程序中使用的javascript,而且还对代码容量作了限制,大的数学计算库没法直接用,只能自己造轮子了。
最小二乘法是一种普遍使用的函数拟合方法,其通过最小化误差平方和来寻找给定数据的最佳函数匹配,尤其适合于函数形式确定的数据拟合。最小二乘法的基本思路:假设有一组实验数据(xi,yi ), 事先知道它们之间应该满足某函数关系yi=f(xi),通过这些已知信息,确定函数f中的一些参数。
例如,如果函数f是线性函数f(x)=ax^2+b, 那么参数 a和b就是需要确定的值。如果用p表示函数中需要确定的参数,那么目标就是找到一组p,使得下面的函数S的值最小:
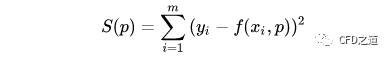
当误差最小的时候可以理解为此时的系数为最佳的拟合状态。
下面是来自百度文库中关于最小二乘法拟合的计算方法(https://wenku.baidu.com/view/a64b55c23c1ec5da50e270d0.html),留此备忘。
设拟合函数为:
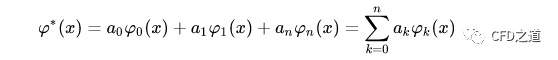
由最小二乘法原则,应使:
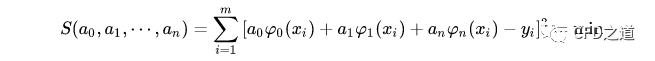
对函数S求偏导数并令其为零,即:
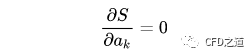
可得到:
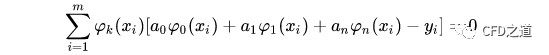
若对于任意函数h(x),g(x)引入记号:
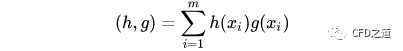
即有:
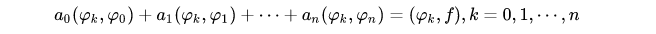
写成矩阵形式为:
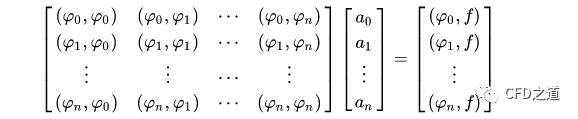
该矩阵方程组称之为法方程组或正规方程组。
当采用多项式进行拟合时,则有:
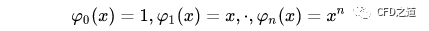
相应的法方程改写为:

求解该线性方程组,可得到a0,a1,…,an等参数值。
若截距为0,则系数矩阵去掉第一行与第一列,变量矩阵与结果矩阵去掉第一个元素。
以一个简单的案例来描述整个过程。
如需要拟合数据表:
| 速度(m/s) | 压力降(Pa) |
|---|---|
| 20 | 197.8 |
| 50 | 948.1 |
| 80 | 2102.5 |
| 110 | 3832.9 |
要将该数据拟合成多项式:
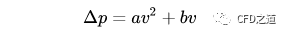
有m=4,n=2。
可以以下轮子代码来解决:
import numpy as np
import matplotlib.pyplot as plt
X = np.array([20,50,80,110])
Y = np.array([197.8,948.1,2102.5,3832.9])
plt.plot(X, Y, 'ro')
# 生成系数矩阵A
def gen_coefficient_matrix(X, Y):
N = len(X)
m = 2
A = []
# 计算每一个方程的系数
for i in range(m):
a = []
# 计算当前方程中的每一个系数
for j in range(m):
a.append(sum(X ** (i + j+2)))
A.append(a)
return A
# 计算方程组的右端向量b
def gen_right_vector(X, Y):
N = len(X)
m = 2
b = []
for i in range(m):
b.append(sum(X ** (i+1) * Y))
return b
A = gen_coefficient_matrix(X, Y)
print(A)
b = gen_right_vector(X, Y)
print(b)
a1, a2 = np.linalg.solve(A, b)
# 生成拟合曲线的绘制点
_X = np.arange(0, 130, 10)
_Y = np.array([a1 * x + a2 * x ** 2 for x in _X])
plt.plot(X, Y, 'ro', _X, _Y, 'b', linewidth=2)
plt.title("y = {}x + {}$x^2$ ".format(a1, a2))
plt.show()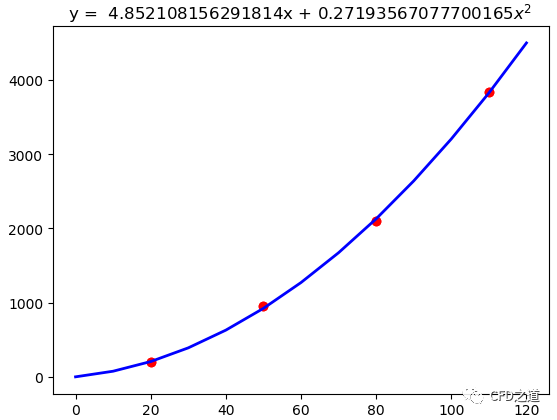
这个拟合结果与excel得到的完全一致。
这里用了numpy中的线性方程求解包linalg。不过对于二元一次方程组,用高斯消去法也就一两句代码的事情。
需要注意并非所有的数据都可以用二阶多项式来拟合,有时候实验数据实在不像话,可能导致最小二乘法最后阶段的线性方程组极度病态,求出乱七八糟的解来。
终于把轮子造完了,javascript代码也搞定,,懒得瘦身了。
//函数参数分别为速度列表与压降列表,类型为数组,确保元素数量一致
Binomialfit: function(velArray, pressureArray) {
//下面要进行函数拟合
//构造AX=B的矩阵方程
var A = new Array();
var B = new Array();
var m = velArray.length; //m为数据点的个数
var sumxx = 0;
var sumxxx = 0;
var sumxxxx = 0;
var sumxy = 0;
var sumxxy = 0; //定义系数矩阵
for (var i = 0; i < m; i++) {
sumxx += Math.pow(velArray[i], 2);
sumxxx += Math.pow(velArray[i], 3);
sumxxxx += Math.pow(velArray[i], 4);
sumxy += (velArray[i] * pressureArray[i]);
sumxxy += (Math.pow(velArray[i], 2) * pressureArray[i]);
}
A.push(sumxx);
A.push(sumxxx);
A.push(sumxxx);
A.push(sumxxxx);
B.push(sumxy);
B.push(sumxxy);
var C = new Array(); //用来放置结果,最终拟合方程为y=C[0]x+C[1]x^2
//直接求解方程,二元一次方程很简单,直接用小学学过的方法解了
//这里要防止分母为零,谁也预料不到用户的输入,没准就碰上了呢
if ((A[1] * A[3] != A[2] * A[1]) && (A[1] * A[2] != A[3] * A[0])) {
C[0] = (B[0] * A[3] - B[1] * A[1]) / (A[0] * A[3] - A[2] * A[1]);
C[1] = (B[0] * A[2] - B[1] * A[0]) / (A[1] * A[2] - A[3] * A[0]);
} else {
wx.showModal({
title: '',
content: '数据矩阵存在问题,无法解析!',
success(res) {
if (res.confirm) {
} else if (res.cancel) {}
}
})
}
return C;
}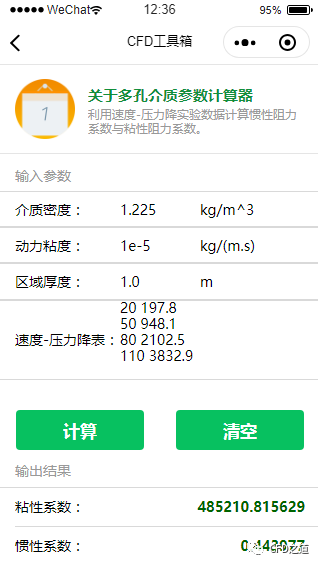
界面做的挫,将就用吧!重新造轮子很是麻烦,估计有N多Bug,懒得去补了~
此文仅为备忘!!
本篇文章来源于微信公众号: CFD之道








评论前必须登录!
注册