本文描述Fluent中提供的宽带噪声模型。

注：本文内容取自Fluent Theory Guide。

”

1 Proudman’s Formula

Proudman^[1]利用Lighthill的声比拟方法导出了无平均流条件下各向同性湍流产生的声功率计算公式。Lilley^[2]考虑Proudman的原推导中忽略的延迟时差重新推导了公式。两种推导得到单位体积产生声功率(W/m3)：

式中，与分别Wie湍流速度与长度尺度；为声速；为模型常数。

利用与可将式(1)改写为：

式中：

在Fluent中，基于Sarkar和Hussaini^[3]在对各向同性湍流进行直接数值模拟的校准，将调整后的常数设为0.1。

Proudman的公式给出了在给定的湍流场中局部对单位体积总声功率的贡献的近似度量。但是在解释结果时应考虑到推导过程中的假设，例如高雷诺数，小马赫数，湍流各向同性和平均运动为零。

2 Jet Noise Source Model

这个轴对称射流的源模型是基于Goldstein^[4] 的工作，其修改了Ribner^[5]最初提出的模型，以更好地解释轴对称湍流射流的湍流各向异性。

在Goldstein的模型中，湍流射流单位体积产生的总声功率由下式计算：

式中，与分别为接收器所在位置的径向坐标和角坐标；为定义的射流单位体积的定向声强，其表示为：

上式中的变量为修正对流系数，其定义为：

且有：

剩余参数定义包括：

式中，及与计算中选择的湍流模型有关。当选择使用RSM模型时，其通过相应的正应力得到。而对于其他双方程湍流模型，其通过下面两个式子得到：

Fluent通过下式输出单位为W/m3及dB的声功率：

式中，为参考声功率，默认情况下。

3 边界层噪声源模型

在低马赫数下，考虑由湍流边界层流过固体而产生的远场噪声通常是由实际意义的。Curle’s integral^[6]基于声类比方法可用于估计固体表面对总声功率的局部贡献。因此可从Curle积分开始：

式中，为发射时间()；为积分面。

之后可以利用以下公式估算远场中的声强：

式中，为相关区域；；为与壁面法向之间的夹角。

整个固体壁面发出的总声功率可通过下式计算得到：

其中，

可以解释为固体表面单位面积对总声功率的局部贡献。表面压力和相关区域的时间导数均方根依据湍流量（如湍动能，耗散率和壁切变）进行近似估算。

4 线性欧拉方程中的源项

线性Euler方程（LEE）可以从Navier-Stokes方程派生得到，该方程从将流动变量分解为均值开始，并假设声学分量远小于流动变量均值及湍流分量。声速分量的线性欧拉方程可以写成：

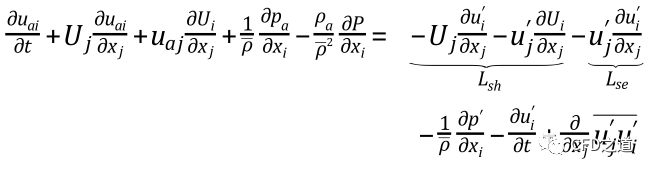
式中，下标表示相应的声学分量；上标表示湍流分离。

上面方程的右侧可以被视为负责噪声生成的有效来源项，其中，涉及湍流的前三项是主要贡献者。前两项表示为通常成为剪切噪声源，因为其涉及到平均剪切。第三项标识为常称之为自噪声源项，其仅涉及湍流速度分量。

利用随机噪声产生及辐射方法(stochastic noise generation and radiation, SNGR^[7] )获取计算LEE源项所需的湍流流场。在giant方法中，湍流速度场及其导数是通过N阶傅里叶模数之和计算得到。

式中，分别为与波数向量相关的傅里叶模数的幅值、相位以及方向向量。

注意LEE中的源项是一个向量，根据当前问题的维度，其具有两个或三个分量。

5 Lilley方程源项

Lilley方程是一个三阶波动方程，该方程可以结合可压缩流体质量与动量守恒推导出来。当忽略粘性项时，该方程可写成：

式中，。

在稳态流动下，Lilley方程可以线性化：

其中，为湍流速度分量。

将其代入前面的方程，得到：

使用SNGR方法合成的平均速度场和湍流（波动）速度分量，可以评估公式中所得的源项。与LEE的源项一样，公式中的源项根据是否涉及平均速度梯度（剪切噪声或自噪声）进行分组，并在Fluent中单独输出。

参考资料