本文描述Fluent DEM模型的一些基础理论及使用方法。

离散元方法（Discrete Element Method，DEM）适用于模拟颗粒物质(如砾石、煤等)。这种模拟的特点是颗粒占有很大的体积分数，颗粒与颗粒之间的相互作用非常重要，而颗粒与流体的相互作用可能重要，也可能不重要。典型的应用包括：料斗、提升管、填充床、流化床、气力输送等。

注：本文内容取自Fluent文档。

”

1 基础理论

DPM模型将移动的颗粒简化为移动的质点，对颗粒形状及其体积进行了模化，计算过程中忽略了颗粒周围的流动细节（例如旋涡脱落、流动分离、边界层等）。基于牛顿第二定律，颗粒运动的控制方程表示为：

DEM基于Cundall及Strack ^[1]的研究工作，考虑颗粒碰撞力的作用（俗称的软球模型）。这些力被归入上面方程的项中。颗粒碰撞产生的力由其变形决定，而变形量是由两对球体之间（或球体与边界之间）的重叠量进行度量，如下图所示。

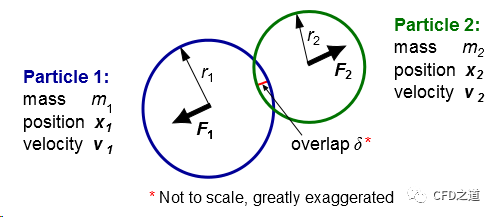
Fluent中可以使用以下形式的颗粒碰撞力：

• Spring
• Spring-dashpot
• Hertzian
• Hertzian-dashpot
• Friction
• Rolling friction

对于给定的碰撞对，法向接触力的弹簧常数的大小至少应满足以下条件：对于该碰撞对中最大的颗粒包及最大相对速度，弹簧常数应足够高以在一个碰撞对中形成两个颗粒包，最大重叠量与颗粒包直径相比不太大。 可以使用以下公式估算弹簧常数的值：

式中，为颗粒包直径；为颗粒质量密度；为两个碰撞颗粒的相对速度；为允许重叠的直径分数。

碰撞时间尺度估计为，其中为颗粒包的质量，定义为。

2 Spring Collision Law

对于线性弹簧碰撞模型，定义单位向量为：

其中，分别为颗粒1与颗粒2 的位置。

重叠量定义为：

其中，分别为颗粒1与颗粒2的半径。

作用在颗粒1上的力可通过下式进行计算：

同样根据牛顿第三定律，作用在颗粒2上的力为：

3 Spring-Dashpot Collision Law

弹簧阻尼碰撞模型在弹簧模型的基础上考虑了阻尼项。因此除了需要指定弹簧常数之外，还需要指定阻尼系数，这里。

为计算碰撞力，先定义一些物理量。

式中，为损失因子；分别为颗粒1与颗粒2的质量；为简化质量；为碰撞时间尺度；分别为颗粒1与颗粒2的速度；为相对速度；为阻尼系数，。

根据前面的表达式，作用在颗粒上的作用力为：

4 Hertzian Collision Law

赫兹碰撞定理^[2]是一个非线性碰撞力，其定义为：

式中，通过颗粒的弹性模量与泊松比计算得到：

式中，分别为颗粒1与颗粒2的弹性模量；分别为颗粒1与颗粒2的泊松比。

5 Hertzian-Dashpot Collision Law

在赫兹碰撞率的基础上考虑阻尼，碰撞力表示为：

6 Friction Collision Law

基于库仑摩擦定律得到：

式中，为摩擦系数；为法向接触力。

摩擦系数为相对切向速度的函数：

• 当：

• 当且：

• 当：

其中，为黏着哦摩擦系数；为滑动摩擦系数；为高速极限摩擦系数；为滑动速度；为极限速度；为一个决定接近的速度的参数。

下图为一个摩擦系数与其影响因素曲线。

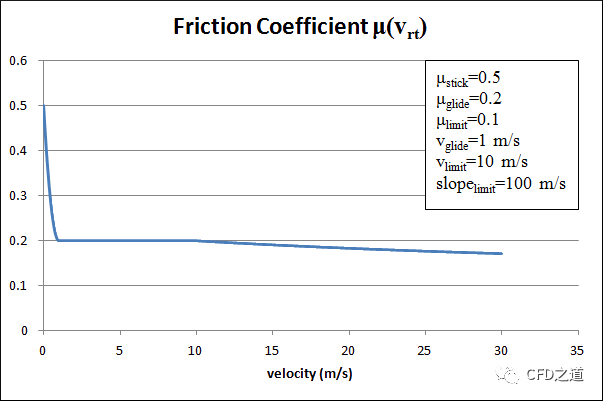
7 Rolling Friction Collision Law

滚动摩擦力计算为：

式中，为滚动摩擦系数；为法向接触力。滚动摩擦力只作用于颗粒-颗粒或颗粒-壁面接触点的局部力矩，根据相对力矩的大小，滚动摩擦力可能会也可能不会抑制相对角速度。

8 Fluent中使用DEM模型

采用以下步骤激活DEM模型。

1、激活DEM模型

在Physical Models选项卡中激活选项DEM Collision，如下图所示。

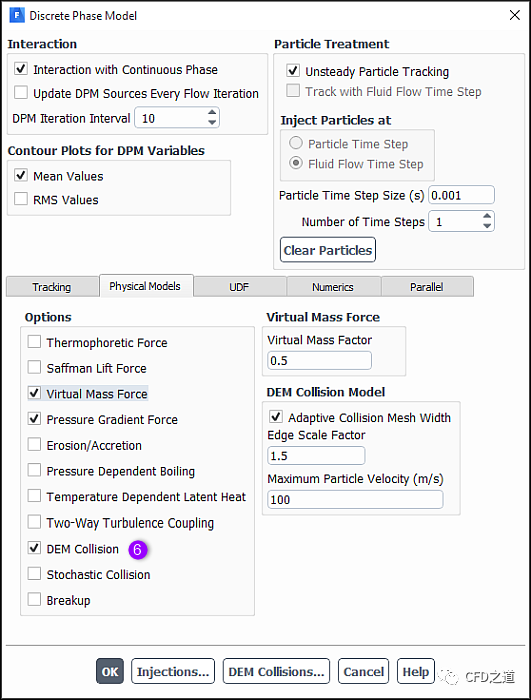
激活模型DEM Collision后，面板中会多出一些DEM Collision Model设置参数;

2、指定碰撞参数

点击按钮**DEM Collisions…**可打开DEM Collisions对话框，在其中创建颗粒碰撞材料属性。

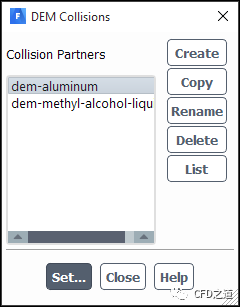
设置法向与切向接触力模型，如下图所示。

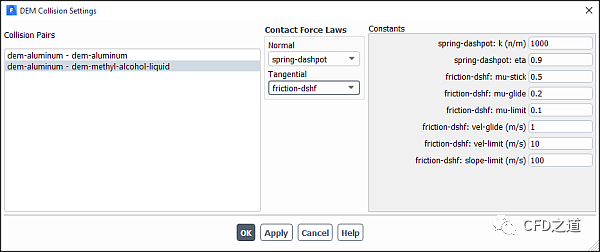
3、指定边界条件

在壁面边界中指定DEM颗粒碰撞对，如下图所示。

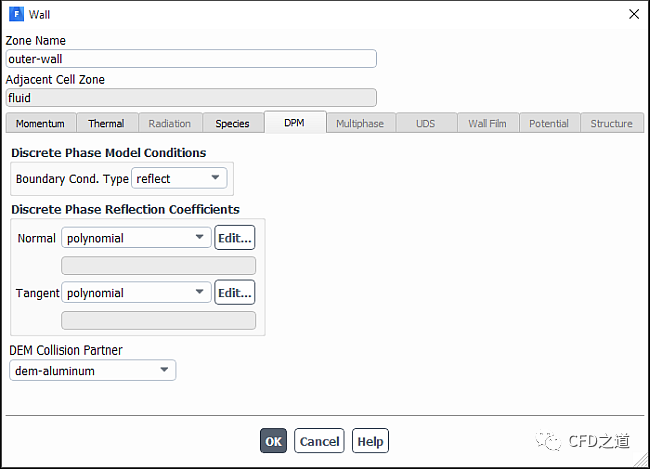
4、DEM模型的一些限制

限制包括：

• 不能使用轴对称几何
• 不能使用动网格
• 不能使用欧拉壁膜模型
• 切应力边界条件不能用于壁面
• Marangoni应力边界条件不能用于壁面
• 在接触过程中DEM颗粒不传递热量

个人观点：就目前来说，Fluent中内置的DEM与其他CFD软件中内置的DEM（如STAR CCM+）相比，最多也就算个玩具，真要做流体与DEM耦合计算的话，利用Fluent+Rocky DEM或Fluent+EDEM耦合是较好的选择。

参考资料