本文描述Fluent中宏观颗粒模型（Macroscopic Particle Model，MPM）所涉及的一些基础理论。

注：

注：本文内容取自Fluent Theory Guide。

”

传统DPM模型适用于颗粒尺寸小到足矣被视为网格单元内的质点，且在流体与内颗粒总体积较少（一般少于10%）的情况下。在这些问题中，颗粒-颗粒以及颗粒-流体之间的相互作用是通过动量、质量以及热量传递进行考虑。然而，当颗粒尺寸大于流体单元时，必须考虑颗粒的体积对流场的影响。Fluent宏观颗粒模型（Macroscopic Particles Model，MPM）能够考虑大(宏观)颗粒的行为以及颗粒与流体、壁面和其他颗粒之间的相互作用。

1 模型概述及局限性

宏观颗粒模型（Macroscopic Particle Model，MPM）是一种基于UDF的跟踪宏观粒子的准直接数值方法^[1]，该模型可以考虑大颗粒在流体中的运动，以及颗粒与颗粒、颗粒与壁面之间的相互作用。MPM模型适用于传统质点颗粒模型无法求解的拉格朗日颗粒流，常用于颗粒尺寸至少为20~30倍网格尺寸场合下。

MPM并非通用模型。该模型在颗粒雷诺数且流体与颗粒的密度比接近1时能够获得比较好的计算结果。对于其他的及的场合，阻力计算可能会不精确，不过当阻力计算不甚重要时也可以使用MPM模型 。

MPM模型提供了一些特殊的处理方式，可以处理如下的问题：

• 流动阻塞与动量交换
• 计算颗粒的阻力和粒径
• 颗粒-颗粒和颗粒-壁面的碰撞与摩擦
• 颗粒的沉积和堆积
• 颗粒-颗粒及颗粒-壁面的吸引力

MPM模型在使用时存在一些局限：

• 无法考虑质量传递及辐射
• MPM与运动/变形网格不兼容
• 由于在每个颗粒时间步内只处理一个碰撞事件，因此不支持对密实度大的粒子进行模拟
• 与DPM粒子没有直接的相互作用(碰撞)
• 可以与多相模型耦合使用，但是需要手动设置源项(质量、动量和热量)
• MPM模型与网格分界面不兼容

2 动量传递

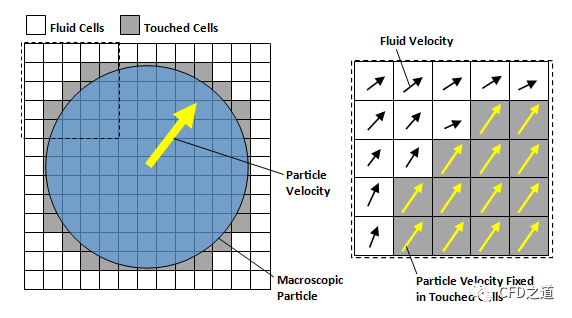
在每个时间步长内，与颗粒相接触的流体单元内的速度通过颗粒速度（平移与旋转）与主流流速之间通过体积分数加权进行计算。另外，所有被颗粒接触的网格单元内的流动速度被强制使用源项从颗粒速度外插到网格中心。因此，与颗粒接触的流体单元中的流速主要由颗粒的速度决定。

3 作用在颗粒上的力与力矩

作用在颗粒上的阻力和力矩通过包含速度、压力以及剪切应力分布的显式表达式来计算。作用在宏观颗粒上的力与力矩在方向上的分量包含虚质量力、压力以及粘性力的分量：

虚质量力分量可表示成：

式中，为单元内流体质量；及为流体及颗粒在方向上的速度；为流动时间步长。

作用在颗粒上方向的压力分量可表示为：

式中，为压力；为与颗粒接触的流体单元的表面积；为从流体网格中心到颗粒中心的向量；为向量沿方向的笛卡尔分量。

粘性力在方向的分量为：

式中，为垂直于平面沿着正方向的剪切应力；为向量在方向的笛卡尔分量。

基于流体作用在颗粒上的力和力矩，在每个流动时间步长内计算新的颗粒位置、速度和加速度。

4 颗粒碰撞

Fluent提供了一种硬球碰撞算法来计算颗粒-颗粒及颗粒-壁面之间的碰撞。所有的碰撞假定是二元的和准瞬态的，并且单点接触。该算法考虑了颗粒在碰撞过程中的冲力和动量，并考虑了能量耗散。

注：

MPM模型使用的是硬球模型。

”

两个粒子在碰撞时的运动可以表示为：

式中，下标1与2表示碰撞的颗粒；为颗粒质量；为颗粒的惯性矩；及分别为颗粒的线性速度与角速度；上标0表示颗粒的在碰撞前的速度；为颗粒半径；为冲力；为法向单位向量。

法向冲力可表示为：

粘滞碰撞的切向冲力表示为：

滑动碰撞的切向冲力表示为：

在上面的方程中，及分别为法向与切向恢复系数；为摩擦系数；为切向单位向量；；为两个颗粒的相对速度（旋转或平移速度）。

5 场力

Fluent MPM模型自动考虑颗粒所受到的重力与福利。

其他颗粒-颗粒的场力，如电磁力、静电力或内聚力等可通过下式进行表示：

式中，为颗粒的质量；为颗粒与之间的距离；为用户指定的颗粒常数。

颗粒与壁面场力定义为：

式中，为颗粒与壁面的最近距离；为自定义颗粒常数。

常数及的正负决定颗粒与颗粒及颗粒与壁面场力是引力还是斥力。

6 颗粒沉积和堆积

对于过滤/分离类型的应用，利用基于临界碰撞速度算法实现粒子沉积和在指定表面堆积的现象的模拟。如果粒子速度低于用户指定的临界冲击速度，则粒子将粘附到壁上， 如果粒子速度高于临界冲击速度，则粒子将从壁面反弹。沉积的粒子被指定零速度和零加速度。

参考资料