接上文DPM｜04 液滴传热与传质[1]，本文描述固体颗粒燃烧过程中的传热与传质。

4 固体脱挥（Law 4）

当燃烧颗粒（Combusting Particle）的温度达到其汽化温度时，且当颗粒的质量大于颗粒中非挥发物的质量时，可以应用Law 4。

Law 4的应用条件为：

且：

式中，为当选择了Wet Combusting时所设置的蒸发/沸腾物料的质量分数（若未选择湿燃烧模型，。如公式（1）所示，当应用Law 4时，沸点与汽化温度应该相等。当激活湿燃烧模型时，与指的是液滴介质的沸点与汽化温度。

Fluent中提供了四种脱挥模型（Devolatilization Models）：

• constant rate model （默认模型）
• single kinetic rate model
• Competing Rates (Kobayashi) Model
• Chemical Percolation Devolatilization (CPD) model

脱挥模型可以在固体颗粒的材料设置对话框中进行选择设置，默认情况下选择的是constant rate model，如下图所示。

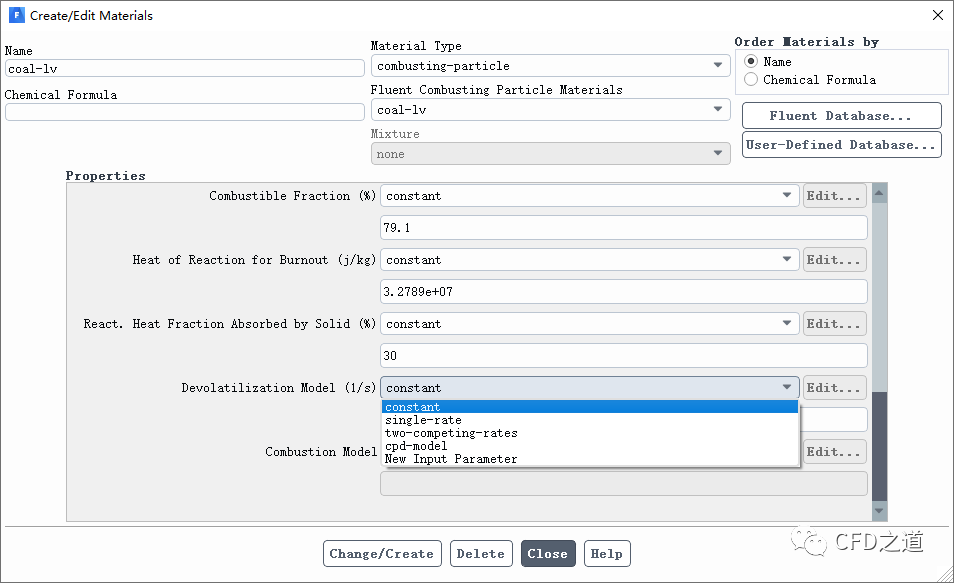
4.1 The Constant Rate Model

恒速率挥发模型指定挥发物以恒定速度释放^[1]：

式中，为颗粒质量，kg；为初始颗粒中的挥发分含量；为初始颗粒质量，kg；为挥发速率，。

速率常数在燃烧颗粒的材料属性中进行指定。Fluent材料数据库中为每种可用的燃烧颗粒材料指定了默认挥发率50 。一个有代表性的挥发速率为12 ，该数据来自于Pillai^[2]对煤燃烧的研究。恰当地使用恒挥发速率要求恰当地设置控制挥发开始的汽化温度。颗粒的挥发分作为挥发性组分进入气相。一旦进入气相，挥发物就会根据输入的气相化学模型进行反应。

4.2 Single-Rate Model

Single Kinetic Rate模型假定挥发速率与颗粒中剩余的挥发分数量有关：

式中，为颗粒的质量，kg；为初始颗粒中的挥发分质量分数；为蒸发/沸腾材料的质量分数（激活了湿燃烧模型）；为初始颗粒质量，kg；为动力学速率，。

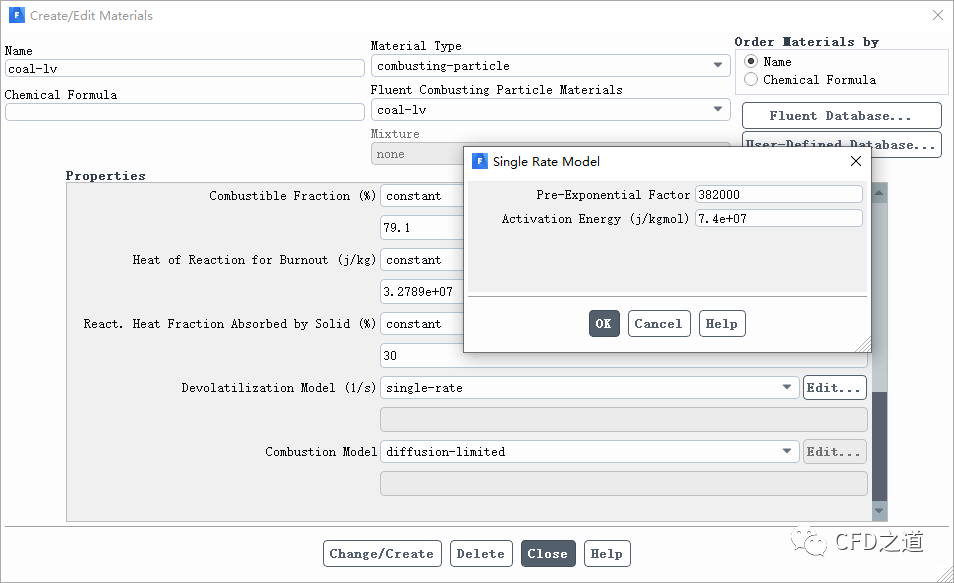
注意，式中颗粒挥发分质量分数应当设置一个比化学分析确定的值稍高的数据；动力学速率通过Arrhenius公式计算（需要指定指前因子及活化能，如上图所示）：

Fluent材料数据库包含速率常数的默认值，以及每种可用的燃烧颗粒材料的默认值。

Single Kinetic Rate模型可以表达为解析格式：

这是通过假设颗粒温度在离散时间步之间只有微小的变化而得到的。

4.3 Two-Competing-Rates Model

Fluent还提供了Kobayashi^[3]所提出动力学挥发率表达式：

式中，及为在不同的温度范围内控制挥发的竞争速率。对这两个动力学速率进行加权，得到了一个挥发率的表达式：

式中，为随时间波动的挥发率；为初始颗粒质量；为产出率；为颗粒中的灰分含量。

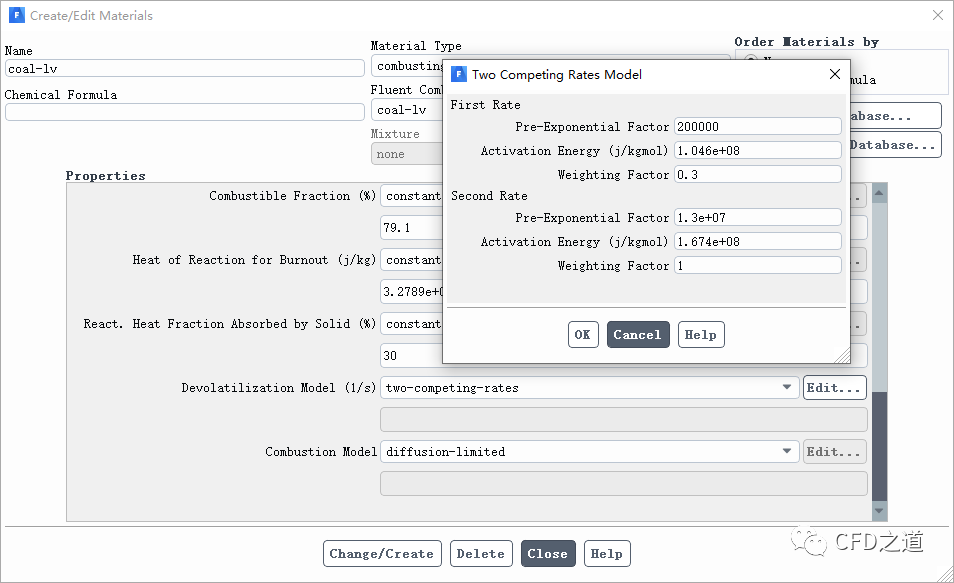
模型需要输入动力学速率参数、、和，以及两个竞争反应的产率及。Fluent对第一(慢)反应的产出率默认值为0.3，对第二(快)反应的产出率默认值为1.0。文献建议设置为近似分析确定的挥发物的比例，因为这个比例代表低温下的挥发。第二个，应该设置得接近1，其为高温下挥发物的产出率。

4.4 CPD Model

在煤热解过程中，煤结构晶格中芳香族团簇之间的不稳定键被裂解，产生两类碎片。一组碎片具有较低的分子量(相应地具有较高的蒸气压)，并以轻气体的形式从煤颗粒中逸出。另一组碎片由焦油气体前体组成，这些前体具有相对较高的分子量(相应的蒸气压较低)，在典型的脱挥条件下，往往会在煤中停留很长一段时间。在此期间，煤晶格的重新连接(称为交联)可能发生。高分子量化合物加上残留晶格称为超质体。煤颗粒的软化行为是由脱挥发过程中产生的超质体的数量和性质所决定的。脱挥发作用后残留的部分晶格结构由炭和矿物复合灰分组成。

这个模型较为复杂，主要用于煤热解过程。详细的理论模型可参阅Fluent Theory Guide。

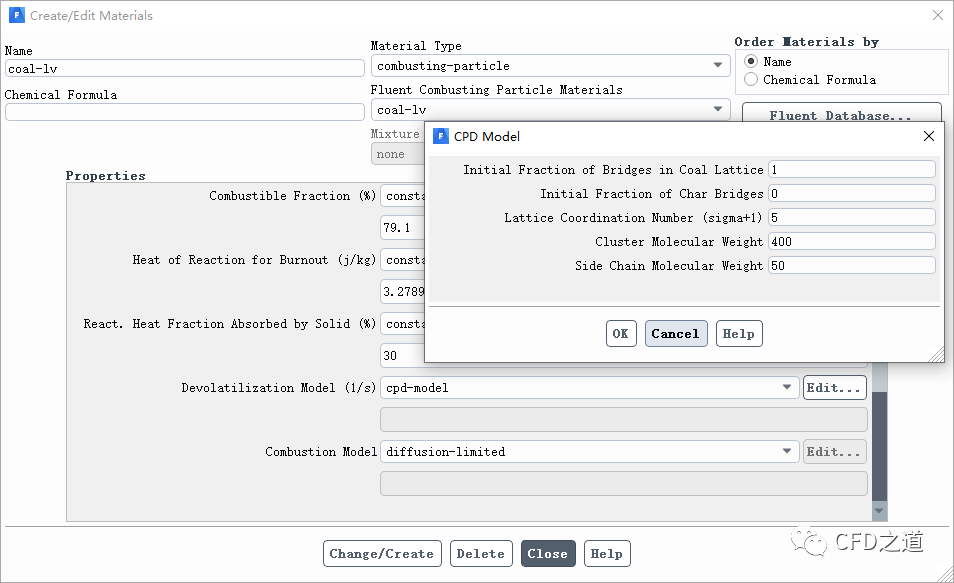
模型输入参数如下图所示：

• initial fraction of bridges in the coal lattice, 
• initial fraction of char bridges, 
• lattice coordination number, 
• cluster molecular weight, 
• side chain molecular weight, 

其中前四个是由NMR实验数据得到的煤结构量。最后一个量是根据煤级来估计的，它代表了原煤中存在的煤焦桥，或者代表了在脱挥过程中很早就形成的煤焦桥。下面是一些不同类型的煤参数（仅供参考）。AR是来自Argonne premium sample bank的8种煤，Sandia指的是Sandia实验室检测的煤炭，AFR为Advanced Fuel Research检测的煤， ACERC是在先进燃烧工程研究中心检测的三种类型的煤。

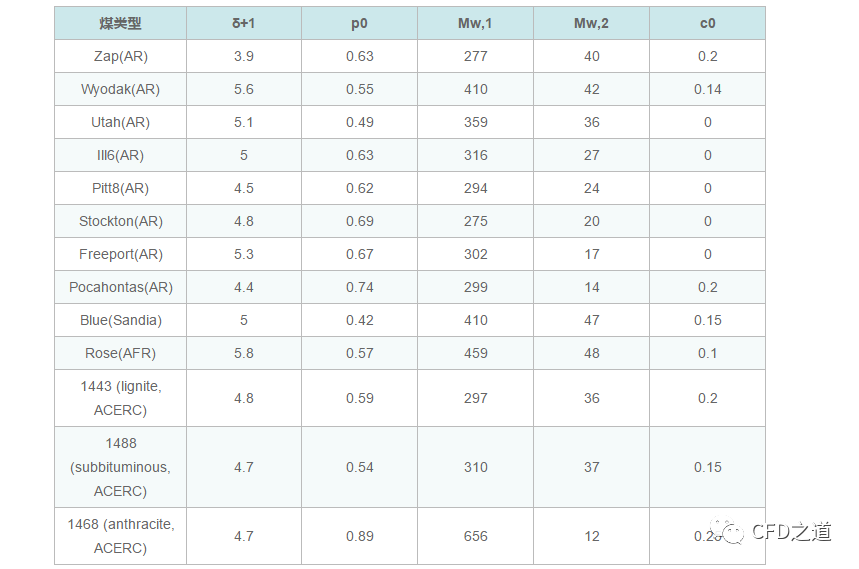
模型参数输入如下图所示。

4.5 颗粒脱挥膨胀

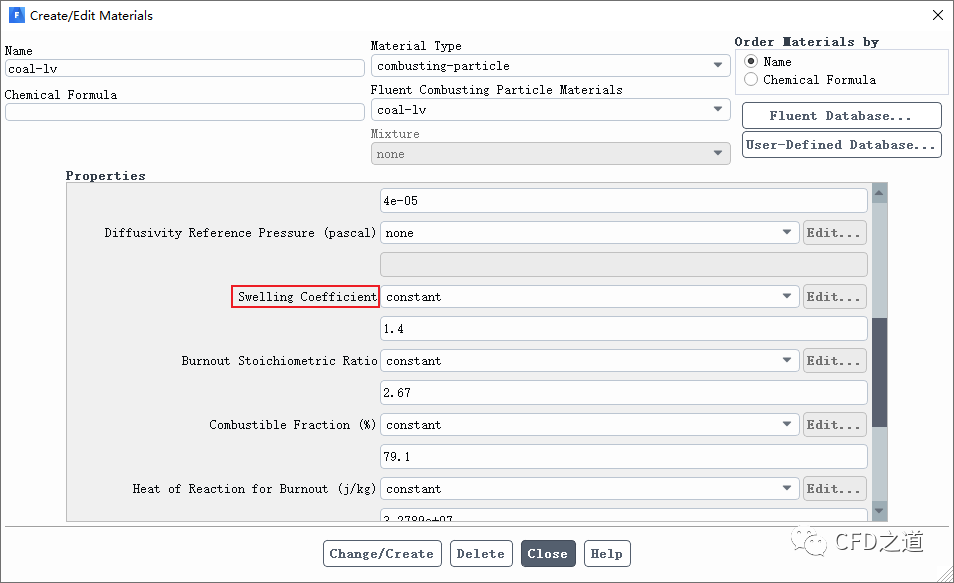
颗粒在脱挥过程中的粒径变化根据用户定义的膨胀系数（Swelling coefficient，）进行计算：

式中，为脱挥之前颗粒的粒径；为当前颗粒粒径。

当膨胀系数为1.0时，粒径保持不变。当膨胀系数为2.0时，挥发分全部汽化后，颗粒粒径增大一倍，当溶胀系数为0.5时，最终粒径为初始粒径的一半。

4.6 脱挥过程中颗粒传热

在脱挥过程中对颗粒的热传递包括对流和辐射(若激活了辐射模型)的贡献:

默认情况下，假设粒子的温度和质量在时间步长之间不发生显著变化，方程通过下面的方式计算:

式中：

由此可以得到脱挥过程中颗粒的温度变化。

5 表面燃烧（Law 5）

当固体颗粒的挥发组分完全挥发后，表面反应开始消耗颗粒的固态可燃部分。此时Law 5开始激活启用。

Law 5的作用范围：

且：

当可燃部分被消耗后，颗粒可能会包含一些残留的灰烬，此时这些可燃灰烬会遵循惰性加热Law 6。

除多表面反应模型外，表面燃烧反应消耗颗粒的反应物含量，其满足表面“燃尽”反应的化学计量要求：

式中，以每质量焦炭的氧化剂的质量来定义，氧化剂和产物的组分在入射器对话框中指定，如下图所示。

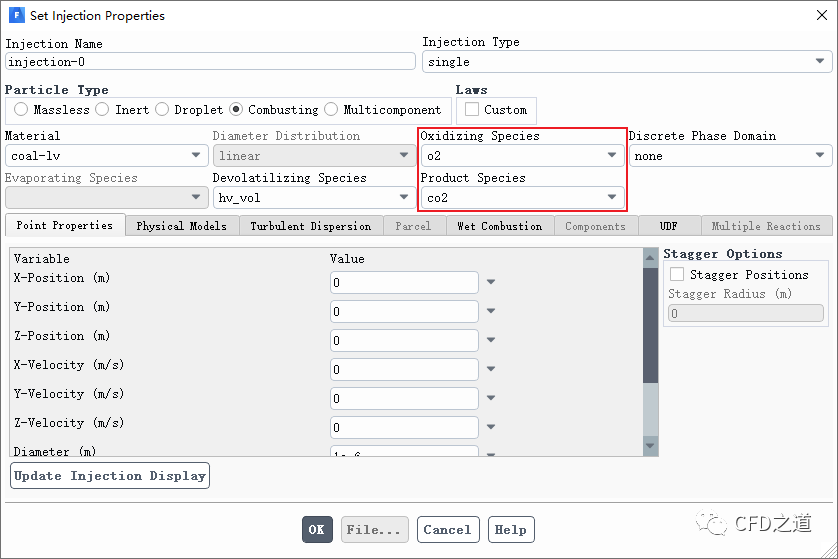
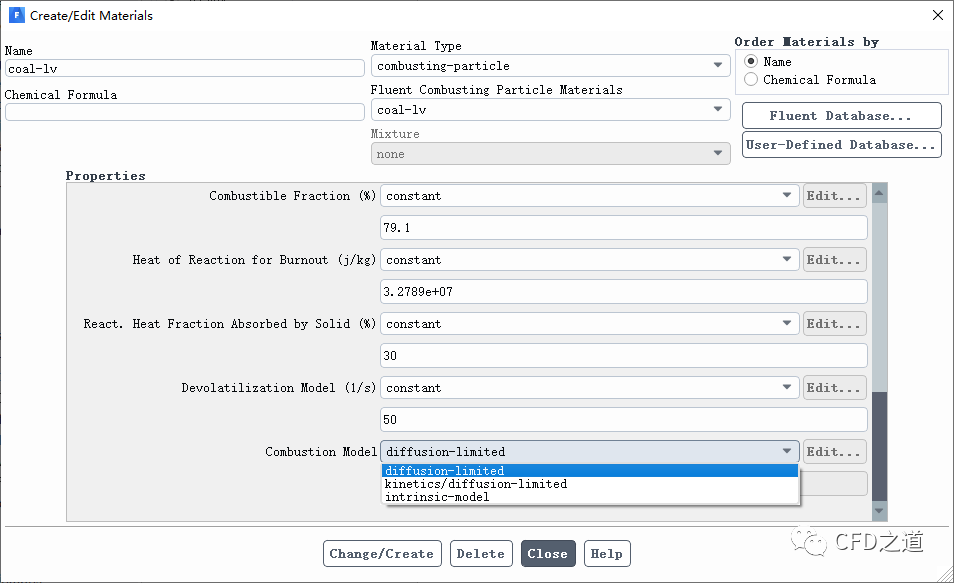
Fluent为燃烧颗粒提供了四种非均相表面反应速率模型：

• diffusion-limited rate model (the default model)

• kinetics/diffusion-limited rate model

• intrinsic model

• multiple surface reactions model

5.1 Diffusion-Limited Model

有限扩散表面反应速率模型是Fluent的默认模型，其假定表面反应速率由气体氧化剂向颗粒表面的扩散决定：

式中，为主流氧化剂的扩散系数，m2/s；为气相中氧化剂的当地质量分数；为气相密度；为化学计量系数。

方程由Baum and Street^[4]模型推导出，其忽略了动力学对表面反应速率的贡献。该模型模型假设颗粒的直径不变。由于颗粒质量减小，有效密度减小，导致炭颗粒的孔隙增大。

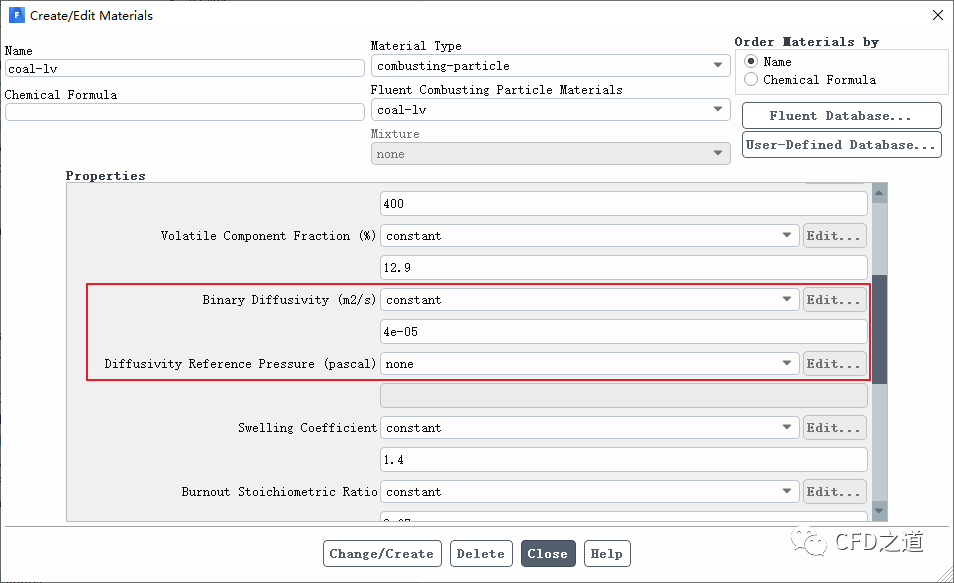
当在Fluent中采用此模型时，需要指定2个参数：

• binary diffusivity：对应模型中的
• diffusivity reference pressure：扩散率参考压力

5.2 Kinetic/Diffusion-limited Model

Kinetic/Diffusion-limited Model假定表面反应速率由动力学或扩散速率决定。Fluent采用Baum和Street模型和Field模型^[5]。

其中扩散速率系数为:

动力学速率为：

焦炭燃烧速率：

式中，为表面积()，为燃烧颗粒周围气体中氧化剂的分压，为动力学速率，包含化学反应对炭颗粒内表面(固有反应)和孔隙扩散的影响。在 Fluent对方上式中的氧化剂质量分数进行了改写：

在此模型中，假设颗粒粒径保持不变，允许密度减小。

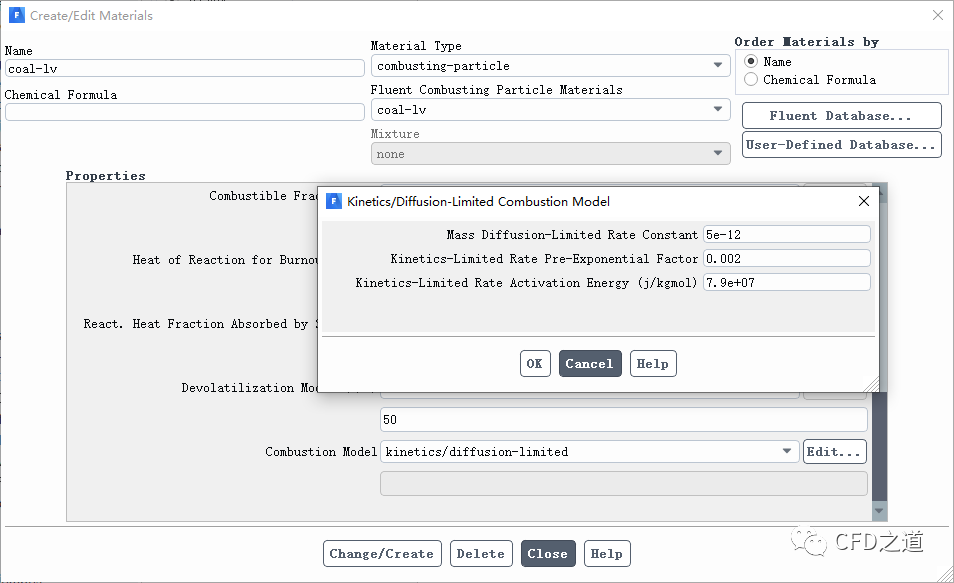
在Fluent中选用此模型时，需要输入3个参数：

• mass diffusion limited rate constant：对应模型中的参数
• kinetics limited rate pre-exponetial factor：对应模型中的参数
• kinetics limited rate activation energy：对应模型参数

5.3 Intrinsic Model

Fluent中的Intrinsic Model基于Smith模型^[6]，模型假设反应的阶次为1。与动力学/扩散模型一样，intrinsic模型假设表面反应速率包括体扩散和化学反应的影响。扩散速率系数采用下式进行计算：

化学反应速率通过下式进行计算：

式中，为有效因子，即在不存在孔隙扩散阻力的情况下，实际燃烧速率与可达到速率的比值：

式中的为：

式中，为主流气体中的氧化剂密度；为颗粒孔隙中的有效扩散系数。

上式中的可表示为：

其中，为分子扩散系数，为颗粒孔隙度:

式中的与分别为热解炭的名义密度与真实密度。

式中为孔隙弯曲度，Fluent中默认值为，对应孔隙与外表面的平均相交角度为45°。

为Knudsen扩散系数：

式中，为颗粒温度；为炭颗粒的平均孔隙半径，可使用汞孔隙度法测定。

为焦炭颗粒的内比表面积，在本模型中假设在焦炭燃烧过程中保持不变。各种热解焦炭的内比表面积数据可见文献^[7]。焦炭燃烧时的内表面积平均值高于热解过程。

定义为Arrhenius形式：

式中为指前因子；为活化能。

为更充分地描述燃烧过程中焦炭颗粒大小(以及密度)的变化，可以指定燃烧模式，将焦炭颗粒直径与燃尽程度联系起来:

其中，为颗粒质量，为颗粒初始质量。

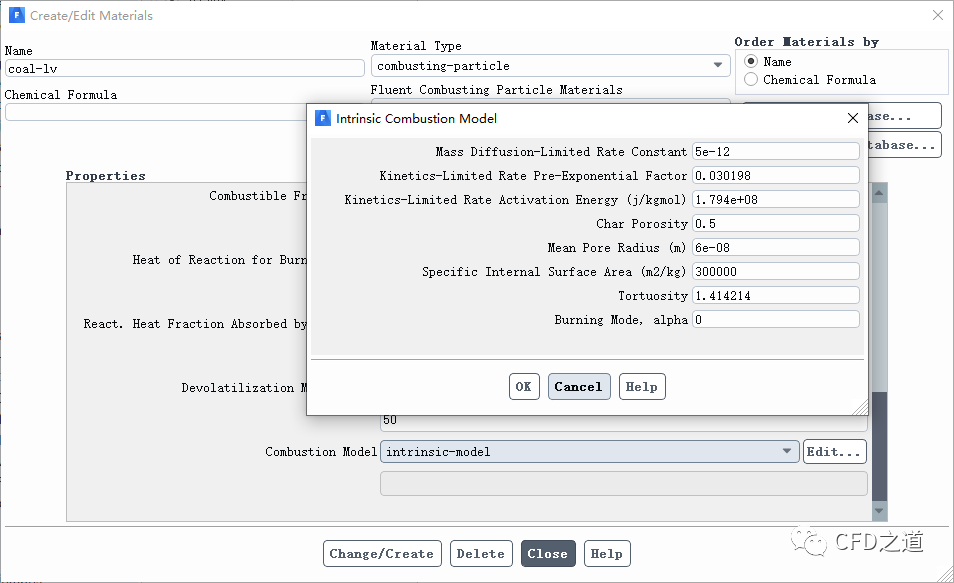
Fluent中intrinsic-model模型参数输入如下图所示。

• mass diffusion limited rate constant：模型中的
• kinetics limited rate pre-exp. factor：模型中的
• kinetics limited rate active energy：模型中的
• char porosity：模型中的
• mean pore radius：模型中的
• specific internal surface area：模型中的
• tortuosity：模型中的
• burning mode：模型中的

参考资料