利用Fluent的离散相模型可以对反应颗粒或液滴进行模拟。Fluent中包含多种传热传质关系,本文将介绍这些关系中使用的物理模型。
注:本文内容取自Fluent Theory Guide。
Fluent中的这些传热传质定律包括:
-
Inert Heating or Cooling (Law 1/Law 6) -
Droplet Vaporization (Law 2) -
Droplet Boiling (Law 3) -
Devolatilization (Law 4) -
Surface Combustion (Law 5) -
Multicomponent Particle Definition (Law 7)
当选择不同的颗粒模型时,将会激活不同的Laws。如下表所示。
| 颗粒类型 | 描述 | 激活的Law |
|---|---|---|
| Massless | - | - |
| Inert | 惰性加热/冷却 | 1,6 |
| Droplet | 加热/蒸发/沸腾 | 1,2,3,6 |
| Combusting | 加热/汽化/挥发/非均相反应 | 1,4,5,6 |
| Multicomponent | 多组分液滴/颗粒 | 7 |
除了系统内置的传热传质律外,用户也可以利用UDF自定义传质传热律。
可以通过选择Wet Combustion来扩展combusting颗粒,使其可以考虑蒸发/沸腾问题。
1 惰性加热/冷却(Law 1/6)
惰性加热或冷却定律(定律1和定律6)适用于颗粒温度低于汽化温度,或颗粒挥发分未完全挥发完时。
这些应用条件可表示为:
-
Law 1
-
Law 6
式中,为颗粒的温度;为颗粒的汽化温度;为颗粒的初始质量;为颗粒挥发后的质量;为颗粒挥发分质量分数。
当使用定律1或定律6时,Fluent使用一个简单的热平衡模型将颗粒温度、对流换热以及颗粒表面的辐射吸收/发射关联起来:
式中,为颗粒质量,kg;为颗粒的比热容,J/(kg.K);为颗粒的表面积,m2;为连续相的当地温度,K;为对流换热系数,W/(m2-K);为颗粒的发射率;为玻尔兹曼常数,;为辐射温度, K。
方程忽略了颗粒内部热阻,假设颗粒内部温度均匀分布。
上面的热平衡方程采用近似的线性化形式进行时间积分,假设粒子温度从一个时刻缓慢地变化到下一个时刻:
在计算颗粒轨迹时,Fluent对方程进行积分,得到下一时刻的颗粒温度:
式中,为积分时间步长,且有:
对流换热系数通过使用Ranz和Marshall关联模型[1]进行计算:
式中,为颗粒粒径,m;为连续相的热导率,W/m-K;为基于颗粒粒径及相对的速度的雷诺数;为连续相的Prandtl数,。
在定律1和定律6中,颗粒/液滴不与连续相交换质量,也不参与任何化学反应。
2 液滴蒸发(Law 2)
定律2用于预测离散相液滴的蒸发。
定律2在液滴的温度达到蒸发温度时开始,一直持续到液滴达到沸点,或者直到液滴中的挥发分已全部挥发完
汽化定律的开始时刻由参数决定。注意,一旦汽化开始(液滴达到温度阈值),其将持续汽化(即使液滴温度降低到以下)。只有当液滴温度低于其露点温度时,蒸发过程才会停止。在此期间,液滴将一直遵循定律2,但无法预测蒸发。当液滴温度达到其沸点时,液滴汽化通过沸腾率预测,此时遵循定律3。
2.1 扩散控制模型
在定律2中,当汽化速率较慢时,质量传递可以认为是由梯度扩散控制的,液滴蒸汽进入气相的通量与液滴表面和本体气体的蒸汽浓度差有关:
式中,为蒸气的摩尔通量,Kmol/m2-s;为质量传递系数,m/s;为液滴表面的蒸气浓度,kmol/m3;为主流相中的蒸气浓度,kmol/m3。
注:Fluent的蒸发定律假设为正(蒸发)。如果存在负的条件(即液滴温度低于露点且存在冷凝条件),则Fluent将液滴视为惰性(此时)。
计算液滴表面蒸气浓度时,假设界面蒸气分压等于液滴温度下的饱和蒸气压:
式中,为普适气体常数。
主流中的蒸气浓度可以从输运方程中计算得到:
式中,为组分的摩尔分数;为局部压力;为主流温度。传质系数通过Sherwood模型计算得到:
式中,为主流中的蒸汽相扩散系数,m2/s;为Schmidt数,;为颗粒粒径,m。
液滴减少的质量通过下式计算:
式中,为组分的分子量,kg/kmol;为液滴质量,kg;为液滴的表面积,m2。
2.2 对流/扩散控制模型
对于高蒸发速率,蒸发介质从液滴表面到主流气相(Stefan流)的对流流动变得非常重要。
Fluent利用下式进行颗粒质量计算:
式中,为液滴质量,kg;为传质系数,m/s;为液滴表面积,m2;为气体密度,kg/m3。
为Spalding质量数,通过下式计算:
其中,为液滴表面蒸气的质量分数;为主流中的蒸气质量分数。
2.3 热解
单速率热解模型使用如下Arrhenius表达式计算液滴向体气相的传质速率:
式中,为液滴质量,kg;为液滴直径,m;为指前因子,kg/s-m;为活化能,J/kg;为颗粒温度,K。
简化的恒速热解模型为:
其中,为速率常数,1/s;为液滴初始质量。
2.4 定义饱和蒸气压及扩散系数
在模型定义过程中,必须将饱和蒸气压定义为温度的多项式或分段线性函数。注意,饱和蒸汽压的定义非常重要,因为其用于获得蒸发过程的驱动力。在问题定义中,应该为整个可能的液滴温度范围内的温度提供精确的蒸气压值。饱和蒸汽压力数据可以从物理或工程手册中获得。
在离散相材料属性设置过程中,必须输入扩散系数。注意,在离散相模型中不会使用为连续相介质指定的扩散系数。
可以将二元扩散系数(binary diffusion coefficient)定义为常数或连续相温度的函数。或者可以将二元扩散系数定义为膜平均温度的函数,该值计算为:
式中,为液滴温度,K;为主流气体温度,K;为平均系数。
也可以选择基于单位路易斯数的假设来让Fluent计算扩散系数:
式中,为气相混合物中组分的质量扩散率;为混合热导率;为混合密度;为混合比热。
根据Polling等[2]的研究结论,对于中低压力(如压力),二院扩散系数与压力成反比,则有:
其中,为组分在参考压力下的二元扩散系数。
2.5 定义沸点及潜热
沸点与潜热是作为液滴介质的常数属性输入的。Fluent中材料数据库中的材料默认沸点对应于该材料在1atm的压力下的沸点。潜热数据对应于该沸点下的潜热。
在蒸发过程中,随着颗粒温度变化,潜热也随着温度的变化而变化:
式中,为沸点,K;为沸点温度条件下的潜热,J/kg;以及分别为气相与液相的比热,J/kg/K。
对于大气压或近大气压条件下的模拟,介潜热随液滴温度的变化一般较小,通常可以忽略不计。若要考虑液滴温度对于潜热的影响,可以在离散相模型对话框中选择选项Temperature Dependent Latent Heat。
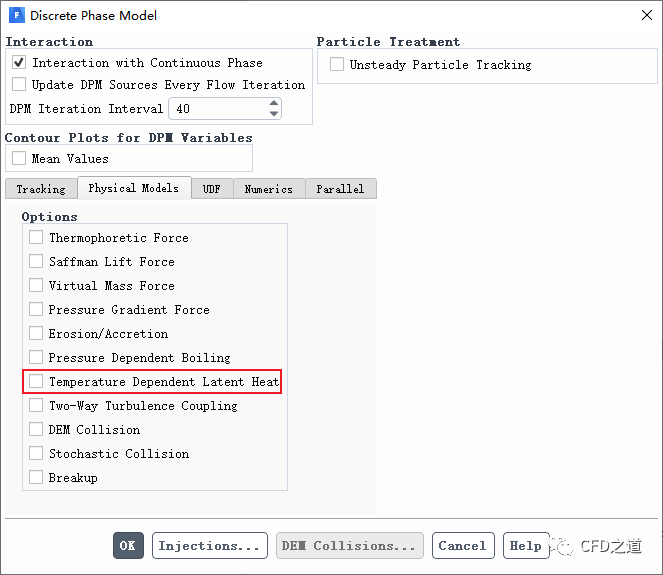
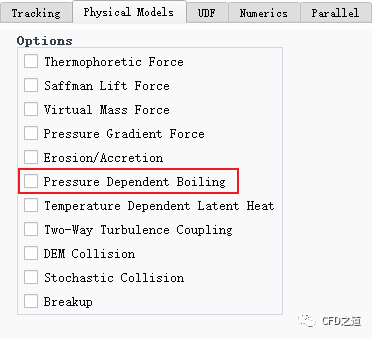
如果模拟中的压力与大气压不同,此时应当修改沸点,使其与液滴蒸发区域的平均压力下的沸点保持一致,或者启用选项Pressure Dependent Boiling。如果修改了液滴材料的沸点,此时也应当相应地修改潜热值。
2.6 传热给液滴的热量
液滴温度根据热平衡计算进行更新,该热平衡将液滴中的显热变化与液滴与连续相之间的对流和潜热传递联系起来:
式中,为液滴的比热容,J/kg-K;为液滴温度,K;为对流换热系数,W/m2-K;为连续相的温度,K;为液滴蒸发率,kg/s;为潜热,J/kg;为颗粒发射率;为波兹曼常数,,为辐射温度,,为入射辐射强度。
只有当激活了辐射模型(P-1或DO模型),并且在DPM模型中激活了选项Particle Radiation Interaction后,传热计算中才会考虑辐射能量。
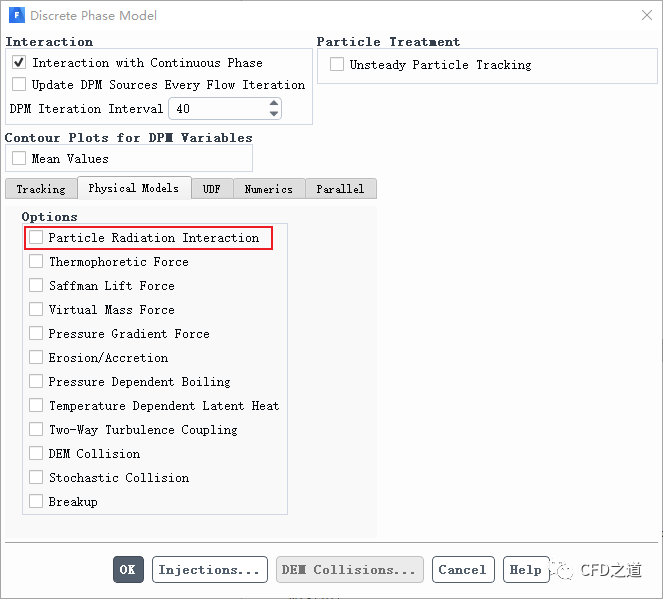
在随后的连续相能量方程的计算中,从颗粒传递到气相或从气相传递到颗粒的热量被作为能量源/汇处理。
采用Convection/Diffusion Controlled model计算汽化率时,上式中的对流换热系数通过修正的数进行计算:
式中,为颗粒粒径,m;为 连续相的热导率,W/m-K;为雷诺数;为连续相的Prandtl数,。
为Spalding传热数,其定义为:
式中,为传递给液滴的热量,W;为液滴蒸发率,kg/s;为液滴蒸汽的比热,J/kg-K。
3 液滴沸腾(Law 3)
当液滴温度达到其沸点时,且液滴中仍含有可蒸发的质量时(液滴质量大于非挥发分的质量),可以应用Law 3预测离散相液滴的对流沸腾。其应用条件表示为:
当液滴温度达到其沸点时,颗粒沸腾速率通过方程计算:
颗粒粒径通过下式计算:
式中,为气相比热容,J/kg-K;为液滴密度,kg/m3;为雷诺数;为连续相的Prandtl数;为气相的热导率,W/m-K。
注:在Fluent 2019R3之前的版本中,上面的公式中Prandtl数采用的是常数0.45。
上式由恒压定常流动条件下推导而来,但要注意,该模型为了保证沸腾现象发生要求,且液滴温度在沸腾过程中始终保持在恒定温度。
当激活辐射模型时,Fluent对上面的方程进行了修改:
当指定沸腾率时,液滴温度被嘉定为恒定温度。液滴蒸发所需的能量在气相能量方程中作为(负)源项出现。
参考资料
W. E. Ranz and W. R. Marshall, Jr. Vaporation from Drops, Part I. Chem. Eng. Prog. 48(3). 141–146. March 1952.
[2]
B. E. Poling, J. M. Prausnitz, and J. P. OConnell. The Properties of Gases and Liquids. McGraw-Hill, New York, 5th edition. 2001.
本篇文章来源于微信公众号: CFD之道








评论前必须登录!
注册