本文介绍Fluent中的5种雾化喷嘴基础理论及其参数设置。
注:内容取自Fluent Theory Guide及Fluent User Guide。
Fluent为液滴喷雾的模拟提供了一些专门的入射模型。与其他常规入射器模型需要指定颗粒的粒径、位置以及初始速度不同,喷雾入射器无需指定这些参数。雾化模型利用喷嘴的物理参数(如喷嘴直径和质量流量)来计算初始液滴的大小、速度及位置。
在真实的雾化器模拟中,液滴在空间上的分散角度以及释放的时间都必须是随机分布的。对于Fluent中非雾化器类型的颗粒入射,所有液滴在时间步开始时沿固定轨迹注入计算区域。雾化器模型采用随机轨迹实现随机分布。
Fluent中提供了5种雾化器模型:The Plain-Orifice Atomizer Model(平口喷嘴雾化模型)、The Pressure-Swirl Atomizer Model(压力旋流雾化模型)、The Air-Blast/Air-Assist Atomizer Model(空气辅助雾化模型)、The Flat-Fan Atomizer Model(转杯雾化模型)及The Effervescent Atomizer Model(气泡雾化模型),可以在入射器创建对话框中选择。
1 平口喷嘴雾化模型
平口喷嘴雾化器是最常见也是最简单的雾化器。然而,喷嘴内部流动及外部雾化的物理过程却并不简单。在Fluent的平面孔板雾化器模型中,液体通过喷嘴加速形成液体射流,之后射流破碎形成液滴。这个看似简单的过程其物理原理却异常复杂。平面孔板可以在三种不同的状态下工作:单相状态、空化状态和Flipped状态[1]。这些状态之间的转换是突然的过程,并且产生截然不同的液滴。喷嘴内部状态决定了喷嘴出口的速度、初始液滴大小和液滴分散的角度。
单相喷嘴流动状态如下图所示,喷嘴内充满了液体。
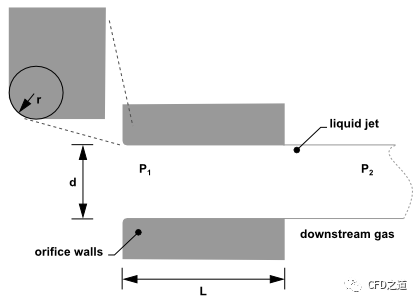
空化状态喷嘴流动如下图所示,喷嘴内在进气口的拐角后形成气穴。
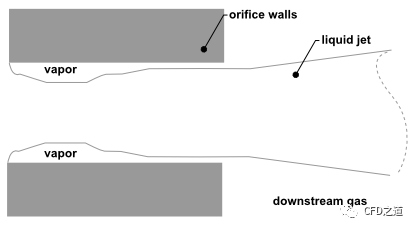
Flipped状态如下图所示,喷嘴内液体射流被气体包裹。
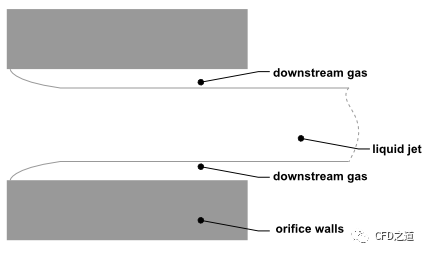
1.1 喷嘴内部状态
喷嘴内部的流动状态对其外部喷雾具有重要对应性,因此为准确的预测喷雾特征,必须正确识别喷嘴内部的流动状态。然而目前还没有一个确切的理论用于确定喷嘴内部的流动状态,很多时候需要依赖于从实验数据中获取的经验模型。Fluent利用几个无量纲参数来确定平面孔板雾化器模型内部的流动状态,这些参数如表所示。
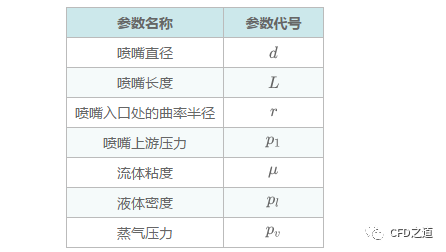
这些参数可以组合成无量纲特征长度,如r/d和L/d,以及基于水力“水头”的雷诺数和空化数()等无量纲数。
收缩系数定义为收缩液流的截面积除以喷嘴总横截面积。Fluent采用下式计算收缩系数:
式中,参数取常数0.611。
1.2 流量系数
描述喷嘴性能的另一个重要参数是流量系数()。流量系数是通过喷嘴的质量流量与理论最大质量流量的比值:
式中,为喷嘴的有效流量,其定义为:
其中,为软件中指定的质量流量,为azimuthal stop angle与azimuthal start angle之差:
其中,azimuthal stop angle与azimuthal start angle均为指定参数。请注意,输入的质量流率应该与指定的开始角度和停止角度相匹配,换句话说应该按照所指定的扇形段指定正确质量流率。若的值为,则有效质量流量与对话框中指定的质量流量一致。
空化数是预测空化开始的一个重要参数。在短尖锐喷嘴中空化产生时。Fluent采用下面的经验公式进行估计:
同样,发生flip时的临界空化数通过下式计算:
若,则一般认为不可能发生flip,此时。利用参数及可判断喷嘴内的流动形态。
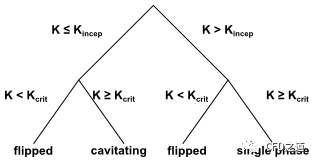
-
单相流动喷嘴()
流量系数通过下式计算:
式中,为极限流量系数,。
-
空化喷嘴()
其流量系数通过下式进行计算:
式中,为前文提到的收缩系数。
-
Flipped喷嘴()
流量系数:
采用迭代法求解喷嘴流量方程,并根据流动状态给出相应的流量系数关系。喷嘴状态可能随着上游或下游压力的变化而变化。喷嘴状态确定后,可以计算出口速度,确定喷雾角度以及初始液滴大小分布。
1.3 出口速度
对于单相喷最,可以通过假设出口流速均匀,利用质量守恒估算出口速度:
对于空泡喷嘴,Schmidt和Corradini[2]已经证明其出口流速不均匀。其推导出了一个空化喷嘴的出口面速度计算公式:
对于Flipped喷嘴,出口速度由质量守恒及减少的流动面积的值来计算:
1.4 喷雾角
喷雾角()通过下式[3]进行计算:
无论是单相喷嘴还是空化喷嘴,喷雾角都取决于气体和液体的密度比以及参数。对于Flipped喷嘴,其喷雾角为常数。
参数必须指定,其与给定喷嘴的形状有关。值越大,喷雾范围约窄。Reitz提出了参数的计算公式:
喷雾角对喷嘴的内部流态非常敏感。因此在实际应用中可能为空化喷嘴选择比单相喷嘴更小的值。典型值范围从4.0到6.0。
1.5 液滴直径分布
入射器的一个关键特征时是液滴大小的分布。对于雾化入射器,液滴直径分布与喷嘴内部状态密切相关。Fluent喷雾模型使用了一个双参数的Rosin-Rammler分布,通过最可能的液滴尺寸及分布参数进行表征,最可能的液滴尺寸有Sauter平均直径[4]得到。
-
单相喷嘴
Wu等[5]利用下式计算:
式中,,其为基于充分发展的紊流管流的射流出口径向积分长度尺度,为韦伯数,其定义为:
式中,为液滴表面张力系数。
-
空化喷嘴
对于空化喷嘴,Fluent对的计算方式进行了细微修改。前面使用的初始射流直径由空化孔板出口的有效面积计算得到,因此定义射流的有效直径。
空化喷嘴的长度尺度,式中定义为:
-
flipped喷嘴
对于flipped喷嘴,初始液滴直径设置为液体射流的直径:
式中,定义为最可能直径。
指定液滴大小分布所需的第二个参数为分布指数。分布指数通常采用经验常数,如下表所示:
| 喷嘴状态 | Spread Parameter |
|---|---|
| 单相 | 3.5 |
| 空化 | 1.5 |
| flipped | ∞ |
Lefebvre给出了rosinr-rammler分布的Sauter平均直径和最可能直径之间的一般关系。
此时,液滴的大小、速度和喷雾角度已经全部确定。
1.6 Fluent输入参数
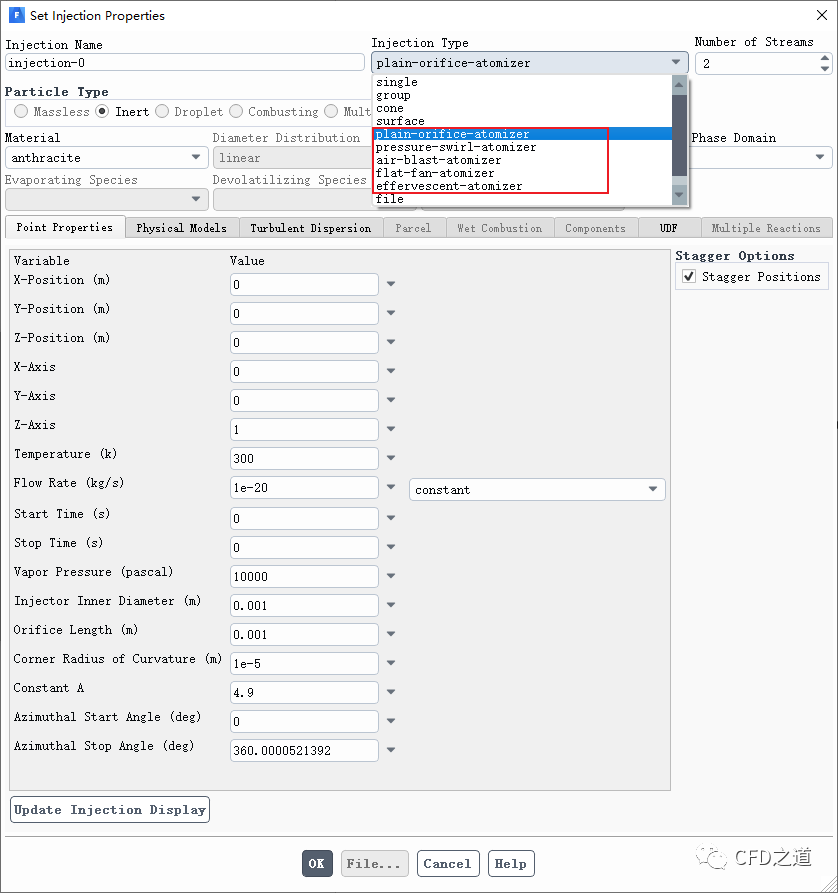
平口喷嘴雾化模型的输入界面如下图所示。

输入参数包括:
-
Position:指定喷嘴所在的空间位置。包括X-Position、Y-Position、Z-Position -
Axis:指定喷嘴轴向的坐标向量,包括X-Axis、Y-Axis、Z-Axis -
temperature:指定颗粒温度 -
Flow Rate:指定颗粒流量。注意此质量流量应与Azimuthal Start Angle及Azimuthal Stop Angle相适应 -
Start Time、Stop Time:指定颗粒入射时间 -
Vapor Pressure:指定蒸气压,对应理论模型中的 -
Injector Inner Diameter:指定颗粒的粒径,对应理论模型中的 -
Orifice Length:指定喷嘴的长度,对应理论模型中的 -
Corner Radius of Curvature:指定入口转角曲率半径,对应理论模型中的 -
Constant A:喷雾角相关参数,对应理论模型中的 -
方位角:包括Azimuthal Start Angle及Azimuthal Stop Angle,指定喷嘴几何的回转角度
2 压力旋流雾化器模型
另一种重要的喷嘴类型就是压力-旋流雾化喷嘴。气体透平工业的人把它称作单相喷嘴(simplex atomizer)。这种喷嘴,然后流体通过一个称作旋流片的 喷头被加速后,进入中心旋流室。在旋流室内,旋转的液体被挤压到固壁,在流体中心形成空气柱,然后,液体以不稳定的薄膜状态从喷口喷出,破碎成丝状物及液滴。在气体透平、燃油炉、直接喷射点火式汽车内燃机的液体燃料燃烧中,压力-旋流雾化喷嘴使用很广泛。液体从内部流到完全雾化的过程可分为三个步骤:液膜形成、液膜破碎及雾滴形成。喷嘴结构如下图所示。
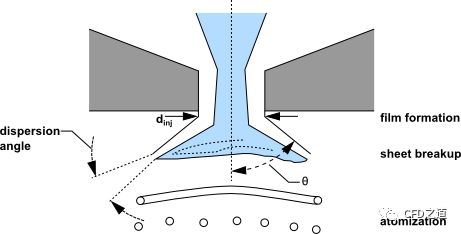
空气和液膜之间的相互作用还没有被很好地理解。目前人们普遍认为是气动力的不稳定性导致了液膜的破裂。数学分析假设Kelvin-Helmholtz波在液膜上增长并最终将液体分解成液带,然后液带由于不稳定性而分裂成液滴。一旦液滴形成,喷雾的演化就由阻力、碰撞、聚结以及二次破碎决定。
Fluent中使用的压力旋流雾化模型使用的是Schmidt等[6]提出的Linearized Instability Sheet Atomization(LISA)模型。LISA模型分为两个阶段:
-
液膜形成 -
液片破碎以及雾化
2.1 液膜形成
液体在喷射器内的离心运动产生了一个被液体薄膜包围的空气核心。喷射器出口处的油膜厚度与质量流量有关:
式中,为喷射器出口直径;为有效质量流量;为喷射器出口位置的轴向速度分量。这些量取决于喷射器的内部结构,很难从基本原理计算出来。假设总速度与喷射器压力有关:
其中,为速度系数。Lefebvre[7]指出,是喷射器器设计和注入压力函数。若将旋流孔视为喷嘴,并假设压力降主要产生于孔口位置,则为流量系数的函数。对于进气角尖锐且为4的单相喷嘴,典型值为0.78或更小。如果喷嘴发生空泡,其值可能低至0.61。因此,0.78可以被认为是的一个实用的上限。其他动量损失大约会使减少10%,其值约0.7。
空气芯尺寸要求为非负意味着对薄膜厚度的约束为:
结合前面的方程课得到轴向速度存在以下约束:
假设喷雾半锥角为,则有,因此可得到的约束关系:
Fluent中,采用下面的方式决定:
假设已知,则可通过式(2)得到,同时可计算出速度:
此时在喷雾器出口处,液膜厚度和轴向速度分量已知。速度的切向分量()等于喷嘴出口下游液膜的径向速度分量。假定喷嘴出口下游速度的轴向分量保持不变。
2.2 液片破碎及喷雾
压力旋流雾化模型包括喷嘴周围气体流动、液体粘度和表面张力对液片破裂的影响。该模型的理论发展细节在Senecal等[8]中给出。
模型假设二维、粘性、不可压的液片厚度,以速度穿过静止的、无粘的不可压缩气体介质。液体及气体的密度分别为及,液体粘度为,坐标系统定义在运动的液片上,将无限小波扰动频谱:
施加于初始定常运动上。扰动频谱导致液体和气体的速度与压力波动。上式中,为初始波振幅;为波数;为复增长率。最不稳定扰动的最大值为,后面将其表示为,并认为其对液片的破碎负责。因此,需要得到一个频散关系,从这个关系中可以计算出最不稳定的扰动。
Squire [9], Li和Tankin[10],以及Hagerty和Shea[11]已经证明存在两种求解模式,其满足上下界面边界条件下的控制方程。第一个计算模式称为反对称模式,在上下界面有同相波。 第二种求解模式称为对称模式,这种模式的波在上下界面的相位不一致。许多作者(例如Senecal等人[12])已经证明,在低速度和低气液密度比的情况下,波的增长主要是由反对称模式决定的。此外在高速流动中对称模式和反对称模式变得难以区分。在Fluent中,雾化模型是建立在液片反对称波生长的基础上的。
如Senecal等推导的,反对称模式的分散关系为:
式中,,。
在临界韦伯数以上(基于液体速度、气体密度和液片半厚度),增长最快的波是短波;当时,波长要比液片的厚度大。现代高压燃油喷射系统的速度足够高,以确保液膜韦伯数远远高于这一临界极限。
忽略二阶粘度项,上式可简化为:
对于与液片厚度相比较长的波,采用[Dombrowski和Johns][12]提出的液片崩解机理。对于长波,一旦非稳定波达到一个临界振幅,就假定液带是在液片破裂过程中形成的。如果扰动在破裂时达到某值,则可以计算破裂时间:
[12]: 12 "N. Dombrowski and W. R. Johns.The Aerodynamic Instability and Disintegration of Viscous Liquid Sheets". Chemical Engineering Science. 18. 203. 1963. "
液片破碎以及液带形成的长度通过下式计算:
式中,是一个关于液片的经验常数,通常需要指定。默认值12由Weber[13]对液体射流的理论计算中得到。Dombrowski和Hooper[14]表明,在韦伯数从2~200的范围内,液片常数为12的值与实验中纸张破裂长度一致。
在断裂点形成的液带直径可通过质量平衡得到。假设液带是由每个波长两次撕裂形成的,那么得到的直径:
式中,为最大增长率所对应的波数。液带直径取决于液片厚度,液片厚度是断裂长度的函数。薄膜厚度由雾化器出口处的破碎长度和从雾化器中心线到液片中间线的径向距离计算:
这种机制不适用于与液片厚度相比较短的波。对于短波,液带直径被假设为与分解液膜的波长成线性比例:
式中,为液带常数,默认值0.5。
在长波或短波情况下,液带到液滴的破裂根据Weber对毛细管不稳定性的分析:
式中,为Ohnesorge数,其为Reynold数与Weber数的组合。一旦从上式确定后,此时假设液滴直径符合Rosin-Rammler分布的液滴大小,其分布指数为3.5,默认分散角为6°。使用此模型时,必须指定喷雾锥角。
2.3 Fluent参数设置
压力旋流喷雾模型的设置对话框如下图所示。
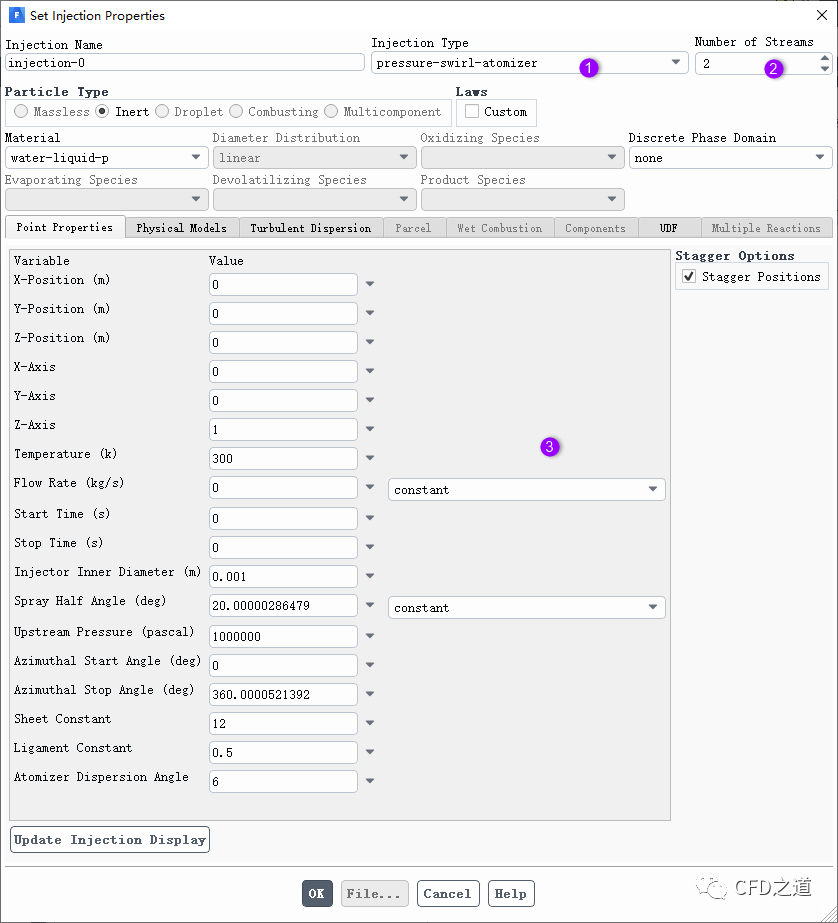
输入参数包括(与平口喷嘴喷雾模型相同的参数,这里不再列出):
-
Spray Half Angle:旋转体的半锥角,对应理论模型中的 -
Upstream Pressure:上游来流的绝对压力,对应理论模型中的 -
Sheet Constant:液片常数,对应理论模型的,默认值12对于Weber数2~200适用 -
Ligament Constant:液带直径 -
Atomizer Dispersion Angle:喷雾分散角。
3 空气辅助雾化器模型
为了加速液膜的破碎,喷嘴经常会添加上辅助空气。液体通过喷座的作用形成液膜,空气则直接冲击液膜以加速液膜的破碎。这种雾化被称为空气辅助雾化 或气泡(air-blast)迸裂雾化(依赖于空气量及其速度)。通过辅助空气的作用,可以得到更小的雾滴。这种提高雾化质量的作用机制并不清楚。一般的看法是,辅助空气加剧了液膜的不稳定性。同时,空气有助于液滴的分散,防止液滴间的碰撞。空气雾化喷嘴同压力-旋流雾化喷嘴一样被广泛应用,尤其是用在要求雾化粒径很小的场合。
FLUENT 中的空气雾化模型由压力-旋流雾化模型所衍生。有个不同点是,在空气辅助雾化模型里,用户需要直接设定液膜厚度。因为空气雾化喷嘴的液膜形成机制很多,所以必须要有此设定。这样,在空气辅助雾化喷嘴模型里就没有压力-旋流雾化模型里所具有的液膜形成方程。
用户还必须设定液膜与空气间的最大速度差。尽管这个量可以计算出来,但设定一个值之后用户就可以不必计算喷嘴的内部流动了。这个特点对大区域(喷嘴相对很小)的流动模拟很方便。
其他方面的设定与压力旋流雾化喷嘴模型的一样。用户必须设定质量流率和喷射角度。液膜离开喷口之后,它的初始轨道沿着设定的喷射角。如果初始液膜的轨道指向中心线,那么,喷射角度为负值。用户还需要设定喷口处液膜的内外半径。
空气辅助雾化模型不包含内部气体的流动。在 FLUENT 中,用户必须把喷嘴内的空气流动设定为边界条件。空气流动可看作一般的连续相的流动,不需要做特别的处理。
雾化器示意图如下图所示:
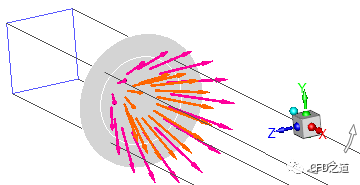
Fluent中设置该雾化器参数的对话框如下图所示:
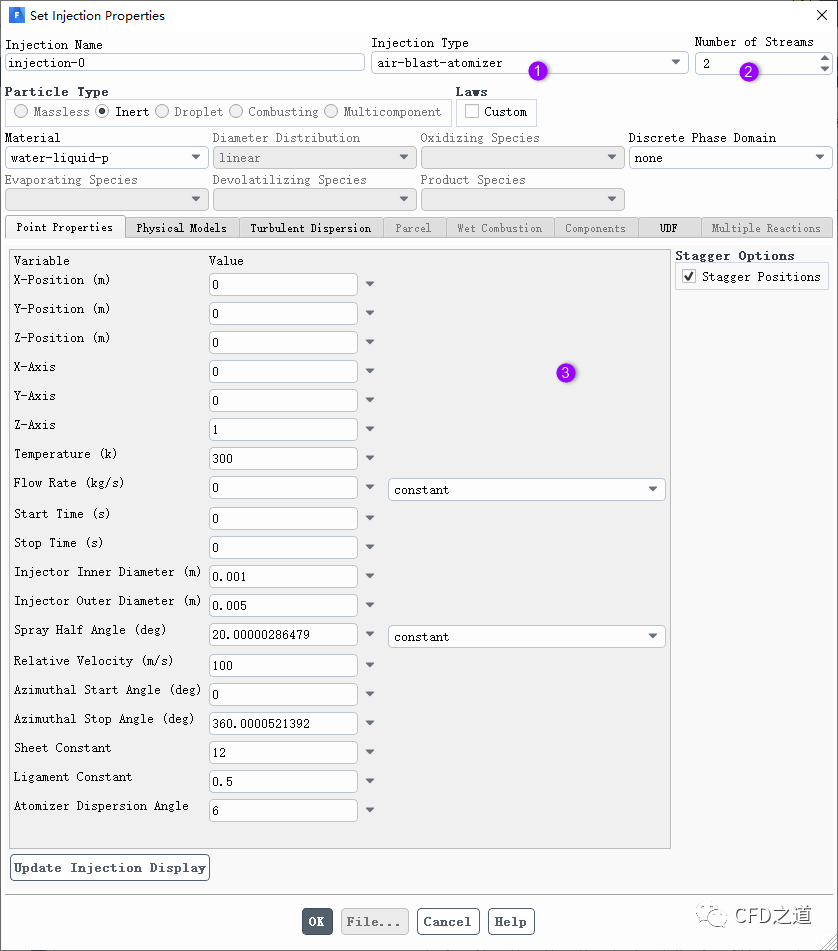
额外的设置参数包括:
-
Injector Inner Diameter、Injector Outer Diameter:雾化器的内外直径,用于计算液片厚度 -
Spray Half Angle:设置液膜离开喷雾孔末端时的初始轨迹,对应理论模型中的 -
Relative velocity:指定液片与空气之间的最大相对速度
4 转杯雾化模型
转杯雾化喷嘴与压力-旋流雾化喷嘴很类似,只不过该喷嘴并非形成旋流,而是形成液膜。液体从宽而薄的喷口出来后形成平面液膜,继而破碎成液滴。一般认为,它的雾化机理与压力旋流雾化喷嘴类似。一些学者认为转杯雾化喷嘴(由冲击射流雾化而来)的雾化机理与平面液膜的雾化类似。在这种情况下,可以应用转杯雾化模型。该模型只能应用与三维的情况下。
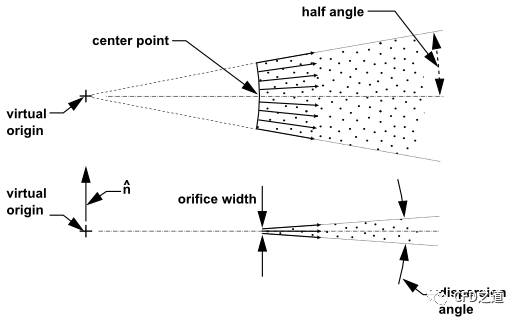
转杯雾化的破碎计算与压力旋流雾化器中液片的破碎计算非常相似。液片分解成液带,然后形成单独的液滴。唯一的区别是对于短波,转杯模型中的液片被假定为在半波长间隔中形成液带。因此对于短波,液带直径为:
其他的处理方式与压力旋流雾化模型一致。
模型设置对话框如下图所示。
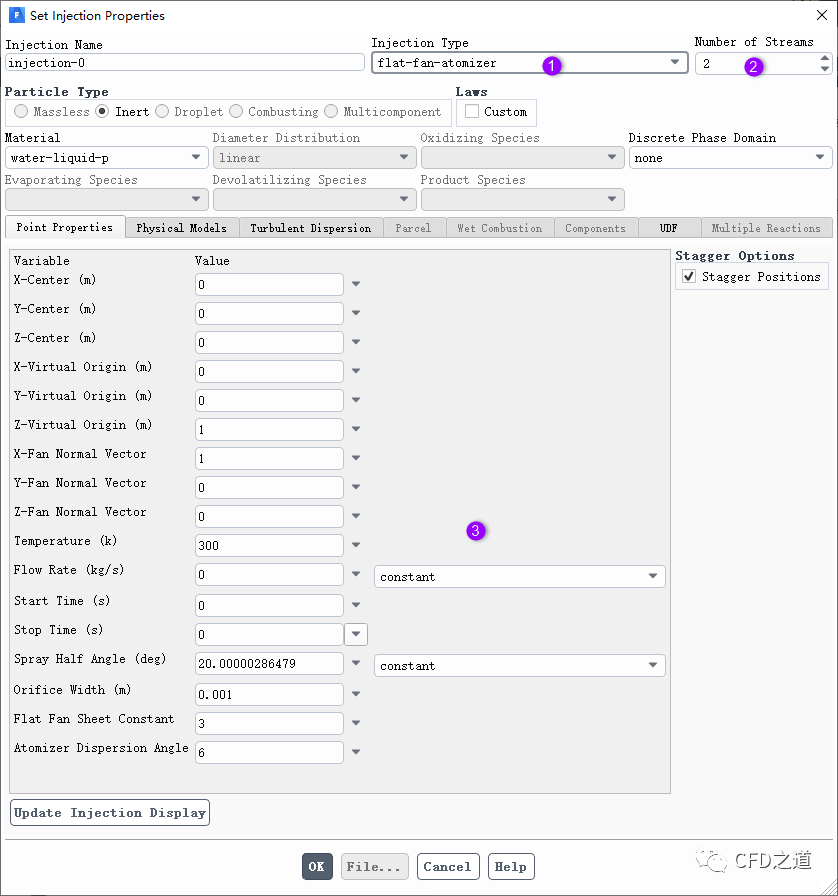
设置参数包括:
-
arc position:设置风扇所在的圆弧的中心点。指定参数X-Center、Y-Center和Z-Center -
virtual position:指定指定风扇所在位置的坐标。指定参数X-Virtual Origin、 Y-Virtual Origin及Z-Virtual Origin -
Normal Vector:指定风扇的法向方向。输入参数X-Fan Normal Vector, Y-Fan Normal Vector及Z-Fan Normal Vector -
Temperature:指定颗粒的温度 -
Flow Rate:指定颗粒质量流量 -
Start Time及Stop Time:喷雾的起始时刻 -
Spray Half Angle:指定当液滴离开喷孔末端时初始的半角 -
Orifice Width:指定喷嘴的宽度
5 气泡雾化模型
气泡雾化喷嘴中,液体中混合了过热液体(相对下游工况)或者类似的介质。当挥发性液体从喷口喷出时,迅速发生相变。相变使流体迅速以很大的分散角破碎成小液滴。此模型也适用于热流体射流。
计算中还必须设定蒸发的气体,此蒸汽是连续相的一部分而不是分散相模型所要处理的。在设定连续相的边界条件时,用户必须在喷口处设定一个连续相的入口边界条件。
液滴的初始速度通过质量守恒计算得到,假设出口射流的截面积是喷嘴面积与的乘积,其中为固定常数,,速度表达式为:
液滴最大直径设置为与出口射流的有效直径有关:
液滴大小从一个分布为4.0的Rosin-Rammler分布中取样。最可能的液滴大小取决于液滴的随机轨迹与注入方向之间的夹角:
式中参数通过下式计算得到:
这一技术创造了一个核心为大液滴,周围为小液滴的喷雾。液滴温度初始化为饱和温度的0.99倍,使得液滴的温度接近沸腾。为了完成模型,闪蒸蒸汽也必须包括在计算中。蒸汽是连续相的一部分,而不是离散相模型的一部分。当指定连续相的边界条件时,必须在注入点处创建一个入口。选择起泡雾化器模型时,除了指定喷射器的位置和方向外,还需要指定喷嘴直径、质量流量、混合量、挥发分物质的饱和温度、喷雾半角和分散常数。
Fluent中设置的模型对话框如图所示。
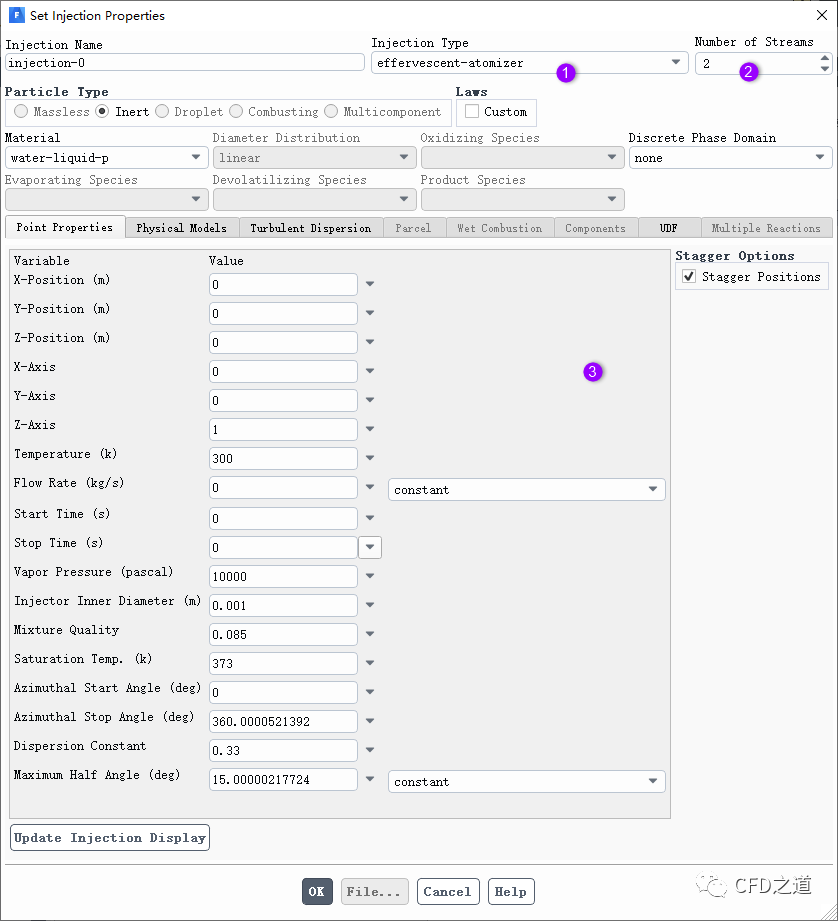
需输入的模型参数包括:
-
mixture quality:设置在混合物质量场中蒸发的混合物质量分数,理论模型中的 -
saturation temperature:设置挥发性物质的饱和温度。 -
droplet dispersion:设置控制液滴大小的空间分布的参数,理论模型中的 -
spray angle:指定喷雾角
关于雾化喷嘴模型,推荐参阅《内燃机计算燃烧学》这本书,总结得非常详细。
参考资料
C. Soteriou, R. Andrews, and M. Smith. Direct Injection Diesel Sprays and the Effect of Cavitation and Hydraulic Flip on Atomization. SAE Paper 950080. SAE. 1995.
[2]D. P. Schmidt and M. L. Corradini. Analytical Prediction of the Exit Flow of Cavitating Orifices. Atomization and Sprays. 7. 6. 1997.
[3]W. E. Ranz. Some Experiments on Orifice Sprays. Canadian Journal of Chemical Engineering. 175. 1958.
[4]A. H. Lefebvre. Atomization and Sprays. Hemisphere Publishing Corporation. 1989.
[5]W. E. Ranz. Some Experiments on Orifice Sprays. Canadian Journal of Chemical Engineering. 175. 1958.
[6]D. P. Schmidt, I. Nouar, P. K. Senecal, C. J. Rutland, J. K. Martin, and R. D. Reitz. Pressure-Swirl Atomization in the Near Field. SAE Paper 01-0496. SAE. 1999.
[7]A. H. Lefebvre. Atomization and Sprays. Hemisphere Publishing Corporation. 1989.
[8]P. K. Senecal, D. P. Schmidt, I. Nouar, C. J. Rutland, and R. D. Reitz. Modeling High Speed Viscous Liquid Sheet Atomization. International Journal of Multiphase Flow. 25(6–7). 1073–1097. 1999.
[9]H. B. Squire. Investigation of the Instability of a Moving Liquid Film. British Journal of Applied Physics. 4. 167. 1953.
[10]X. Li and R. S. Tankin. On the Temporal Instability of a Two-Dimensional Viscous Liquid Sheet. Journal of Fluid Mechanics. 226. 425. 1991.
[11]W. W. Hagerty and J. F. Shea. A Study of the Stability of Plane Fluid Sheets. Journal of Applied Mechanics. 22. 509. 1955.
[12]P. K. Senecal, D. P. Schmidt, I. Nouar, C. J. Rutland, and R. D. Reitz. Modeling High Speed Viscous Liquid Sheet Atomization. International Journal of Multiphase Flow. 25(6–7). 1073–1097. 1999.
[13]C. Weber. Zum Zerfall eines Flüssigkeitsstrahles. ZAMM. 11. 136–154. 1931.
[14]N. Dombrowski and P. C. Hooper. The effect of ambient density or drop formation in sprays. Chemical Engineering Science. 17. 291–305. 1962.
本篇文章来源于微信公众号: CFD之道








评论前必须登录!
注册