本文描述DPM模型中常用的阻力模型。

注：本文内容取自Fluent Theory Guide。

流体作用在颗粒上的阻力/曳力可表达为下面的形式：

对于阻力的计算主要是体现在阻力系数上。Fluent提供了多种不同的模型用于阻力系数的估计。如下图所示。

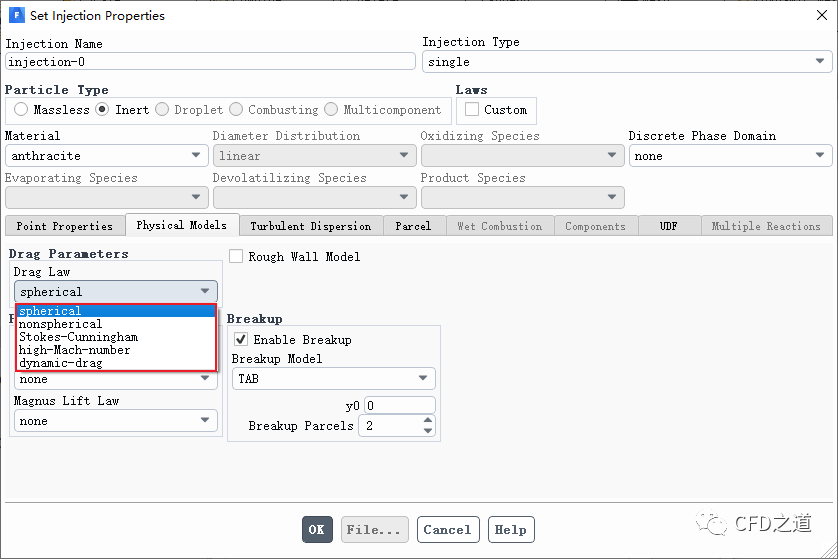
1 Spherical阻力

对于光滑颗粒，其阻力系数考虑为：

式中，为常数，Morsi and Alexander^[1]给出了一些不同雷诺数范围内的常数值。

2 Non-spherical阻力

对于非球形颗粒，[Haider and Levenspiel][2]提出了下面的关系式：

[2]: 2 A. "Haider and O. Levenspiel. Drag Coefficient and Terminal Velocity of Spherical and Nonspherical Particles. Powder Technology. 58. 63–70. 1989."

式中，

其中，为形状因子，其定义为：

式中，为与具有相同体积的球形颗粒的表面积，为颗粒的实际表面积。为了计算颗粒质量、阻力和，颗粒粒径应为具有相同体积的球体的直径。

注：形状因子不能大于1。

3 Stokes-Cunningham阻力

对于亚微颗粒，Stokes阻力公式^[2]可表示为：

式中，参数为Stokes阻力公式的Cunningham修正系数，其计算方法为：

其中，为分子平均自由程。

4 High-Mach-Number阻力

高马赫数阻力定律与球形颗粒的表达形式类似，在马赫数超过0.4，颗粒雷诺数超过20时进行修正^[3]。

5 Dynamic阻力

Fluent提供了一种动态确定液滴阻力系数的方法，能够考虑了液滴形状的变化对阻力的影响。

Dynamic阻力模型几乎能够适用于任何情况。该模型与TAB及Wave液滴破碎模型能够很好的兼容。当碰撞模型被激活时，碰撞过程会设置液滴由于碰撞而产生的畸变以及畸变速度。

许多液滴阻力模型假设液滴在整个计算区域内保持为球形。根据这个假设，一个球形物体的阻力系数^[4]可通过下式确定：

然而，初始形状为球形的液滴在气体中运动，当韦伯数较大时，其形状会发生明显的变形。在极端情况下，液滴的形状可能接近于圆盘的形状。然而，圆盘的阻力比球体要大得多。由于液滴的阻力系数高度依赖于液滴形状，因此将液滴假设为球形而获取的阻力模型无法令人满意。Dynamic阻力模型能够考虑了液滴形状畸变对阻力的影响，即在球体阻力系数（上面的方程）及圆盘阻力系数对应的1.54之间线性变化：

式中，为液滴的畸变，通过下面公式计算得到：

在无畸变()的极限条件下，得到的是球体的阻力系数，在最大畸变()下，得到圆盘所对应的阻力系数。

6 稠密离散相阻力模型

Fluent稠密颗粒流动的阻力律主要有Wen和Yu、Gidaspow和Syamlal-O 'Brien模型。这三种模型都依赖于颗粒相体积分数。

注意这三种模型只能用于稠密离散相模型中。

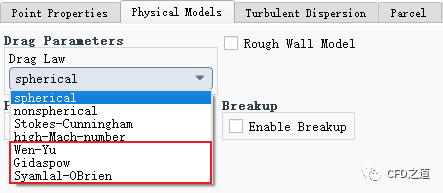
关于这几个模型，在后面的稠密离散相模型中再详细描述。

7 旋转阻力模型

Fluent可以考虑流体作用在旋转颗粒上的旋转阻力。

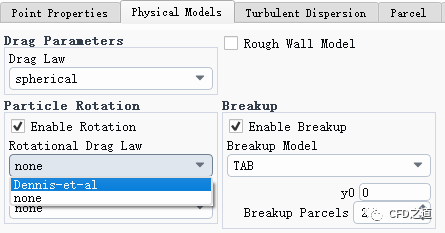
旋转阻力系数可通过Dennis et al. ^[5]提出的模型进行计算：

该模型适用于旋转雷诺数。

旋转雷诺数可通过下式计算：

参考资料