本文描述Fluent中冲蚀计算的相关理论。

内容来自Fluent Theory Guide。

冲蚀是由于壁面微小机械变形或开裂从而导致材料移除的过程。在携流设备中(如燃气轮机、水轮机、水泵、换热器等)，发生表面冲蚀的部分原因是流体中夹带的固体颗粒对设备壁面的冲击。壁面冲蚀会导致设备性能下降、老化以及使用寿命缩短。

对于脆性材料，冲蚀主要是由于壁面材料发生开裂和剥落而产生；而对于韧性材料，冲蚀是通过一系列重复的微塑性变形而产生的，韧性材料的最高的冲蚀率通常发生在冲击角度为20-30°^[1]。

壁面材料的抗冲蚀能力取决于其在冲击下的变形能力，以及下面列出的其他一些可能因素，这些因素包括：

• 颗粒冲击速度
• 颗粒冲击角度
• 壁面材料的力学属性（如制造工艺、微观结构特征等）
• 壁面温度
• 颗粒与目标之间的摩擦系数
• 由反弹颗粒引起的屏蔽效应

文献中的实验冲蚀数据往往存在较大的不确定性。不同作者所报告的冲蚀率可能会有很大的差异（甚至对于相同的材料也会有数量级的差异^[2]）。

Fluent提供了一些冲蚀模型用于计算颗粒冲击壁面造成的损伤，这些模型包括：General、Finnie、Oka、McLaury以及稠密颗粒的磨蚀。

1 Finnie冲蚀模型

对于几乎所有的韧性材料，冲蚀都随冲击角和速度的变化而变化：

式中，为无量纲冲蚀冲蚀质量；为模型常数；为颗粒冲击速度；为关于冲击角的无量函数。对于金属材料，指数通常取值为2.3~2.5弧度。

Finnie冲蚀模型利用下列函数将冲蚀率与颗粒冲击壁面的动能联系起来：

Fluent中Finnie冲蚀模型的缺省常数仅适用于砂粒冲击碳钢壁面时的侵蚀计算。模型常数的值已经调整到与文献^[3]中描述的实验相匹配，在该实验中，326 μm的沙粒以104 m/s的速度撞击碳钢壁面，因此默认常数计算的结果仅在此特定条件下是有效的。

2 Oka冲蚀模型

在Oka冲蚀模型中，冲蚀率定义为：

式中，为冲击角为90°时的参考冲蚀率；为颗粒冲击角度；为参考速度；及分别为颗粒粒径及参考粒径；及分别为速度指数与粒径指数；为冲击角函数。

冲击角函数定义为：

其中，为壁面冲击角，弧度；为壁面材料的维氏硬度；GPa；及为角度函数常数。

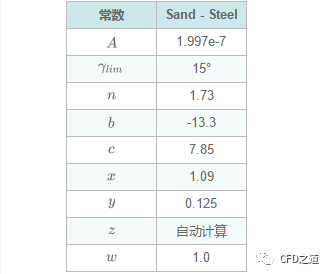
Oka模型常数示例如下表所示。

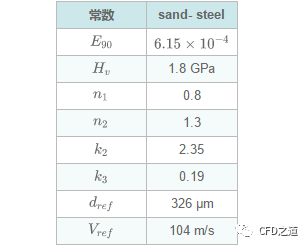
3 McLaury冲蚀模型

McLaury^[4]提出了一种预测水中砂冲蚀率的模型，该模型主要用于模拟泥浆侵蚀过程中的侵蚀速率。McLaury冲蚀率表示为:

式中，为经验常数；为颗粒冲击速度；为壁面材料的布氏硬度；为指数，对于碳钢材料k=-0.59，对于其他材料需要通过试验测定。

冲击函数定义为：

模型常数以及都需要通过实验才能测定。用于使函数在处保持连续。

上面文献中给出的模型常数只对水沙悬浮液有效。颗粒碰撞速度假定在0-10米/秒范围内。

3 General冲蚀模型

颗粒冲蚀和附着速率可以在壁面边界上进行监测。侵蚀率定义为：

式中：为颗粒直径的函数；为颗粒路径与壁面的冲击角；为冲击角的函数；为颗粒相对速度；为颗粒相对速度的函数；为壁面网格面积。默认值。需要注意，被定义为壁面边界条件，而不是壁面材料的属性，因此默认值不会根据所选用的材料而更新。用户应当根据自己的问题去设置这些参数。Edwards等^[5]给出了砂粒对碳钢及铝的冲蚀时的参数。

参数的函数必须用分段线性、分段多项式或多项式函数来表示，以便将它们定义为壁面边界条件的一部分，因此可能有必要用这些方法来近似文献中的函数。

上面计算的侵蚀率以去除材料的质量/(面积-时间)的单位表示，即质量通量，因此可以根据Fluent中定义的单位进行相应的改变。函数和必须以一致的单位指定，以建立一个无量纲的相对粒子速度及其指数。要计算以长度/时间(例如，毫米/年)表示的侵蚀率，您可以定义一个自定义场函数来将侵蚀率除以壁面材料的密度。

多种冲蚀模型（文献^[6]、文献^[7]、文献^[8]、文献^[9]、文献^[10]、文献^[11]）包含模型常数（文献^[12]、文献^[13]）和冲击角函数，可以方便地在Fluent中实现。描述某些冲蚀模型的方程也可以修改为描述侵蚀率的通用方程。

例如，Tulsa模型^[13]模型定义为：

可以根据General模型的形式进行改写：

其中，为冲蚀率（单位质量单位面积的冲蚀质量）；B为材料的布氏硬度；为颗粒的形状系数。Tulsa模型建议参数对于锐角砂粒取值1.0，对于半圆形砂粒取值0.53，对于完全圆形的砂粒取值0.2。

如前所述，冲击角函数可以用分段多项式拟合来近似。下面是钢受砂粒冲蚀时的冲击角函数的近似值：

利用UDF函数可以描述任何形式的冲蚀模型。对于更复杂的模型，如不能仅用线性或多项式函数拟合的模型，则无法使用“壁面边界条件”对话框中的缺省侵蚀模型，此时可以使用UDF宏DEFINE_DPM_EROSION进行指定。

注意只有在启用耦合计算时，才能显示颗粒冲蚀率和附着率。附着率定义为：

4 稠密颗粒流中的冲蚀率

在稠密颗粒流动中，由于近壁面固体颗粒层的屏蔽作用，颗粒间的相互作用可能会影响冲蚀速率。此外，固体颗粒几乎平行于壁面移动可能导致磨蚀。在Fluent中，稠密颗粒系统的总冲蚀率计算如下:

其中，为固体颗粒对壁面的磨蚀；为考虑屏蔽效应下的颗粒对壁面的冲蚀。

以下情况下激活冲蚀和磨蚀计算：

• 在DPM相中激活选项Erosion/Accretion
• 至少包含一个分散颗粒欧拉相

在许多壁面侵蚀的情况下，颗粒倾向于在近壁面区域集中成条纹状，这严重地违反了分散流态的基本(和基本)DPM假设。为了采用拉格朗日方法模拟密集的颗粒，必须考虑颗粒与颗粒间的相互作用以及颗粒的体积位移，这可以通过在颗粒密集区域使用DEM模型实现，然而DEM模型计算成本非常高，为了避免这种开销，Fluent使用分散欧拉相考虑体积位移及相间相互作用，分散欧拉相被认为可以充分代表近墙壁的颗粒的行为。侵蚀率由欧拉相的相关物理量(如壁面剪切侵蚀)来计算，根据Finnie、Oka和McLaury模型计算出的经典DPM冲蚀混合屏蔽功能进行衰减。

4.1 颗粒磨蚀

将固相在近壁面区域的磨蚀过程模拟为固相壁面剪切应力和固相近壁面速度的函数：

式中，为经验常数；为固相速度；为速度指数；为固相剪切应力；为固相体积分数；为固相颗粒的充填极限（对于球形颗粒，约为0.63）。

对于N个颗粒相的多相流动，由于壁面剪切应力引起的侵蚀率为各颗粒相的累积侵蚀率:

4.2 壁面屏蔽效应

在稠密颗粒流动中，接近壁面的颗粒可能会减速，或者被附近与壁面几乎平行运动的其他固体颗粒反弹。这种屏蔽作用会降低颗粒撞击固体壁面造成的冲蚀率。

为考虑这种影响，在Fluent中使用屏蔽因子：

其中，为固相颗粒的体积分数；为充填极限（球形颗粒约0.63）。

计算冲蚀率时，使用屏蔽因子对单向冲蚀率进行缩放：

当局部固相体积分数接近堆积极限时，壁面将受到保护，不受任何颗粒的冲击，即冲蚀率为零。

对于N个颗粒相的流动，屏蔽作用是由单个欧拉体积分数之和计算：

参考文献