Fluent的网格自适应功能能够基于几何及计算结果对网格进行细化和/或粗化。本文描述Fluent中的网格自适应功能。

本文取自Fluent Theory Guide。

1 网格自适应过程

网格自适应过程包括两个任务：

• 通过几何和/或求解结果创建自适应函数对网格进行标记
• 基于自适应标记对网格进行细化或粗化

注：建议在网格自适应之前保存cas及dat文件，防止在网格自适应过程中生成了不合适的网格。

Fluent中提供了两种网格自适应方法：

• 悬挂节点自适应

此方法基于预定义模板各种类型网格进行细化或粗化。悬挂节点自适应方法无法加密多面体网格，且需要额外的内存来保存网格细化过程中层次结构。

• 多面体非结构网格自适应（Polyhedral Unstructured Mesh Adaption，PUMA）

该方法将所有网格类型视为多面体，并应用统一的网格细化方法。该方法不创建悬挂节点，因此在使用过程中比悬挂节点自适应方法内存消耗更少。PUMA方法通常只用于3D网格（默认情况），也可用于2.5D网格（一个单元厚度的网格）。

1.1 悬挂节点自适应

悬挂节点自适应（Hanging node Adaption）常用于2D网格，不过在3D网格中也能选用。该方法生成不共享节点的计算网格，如下图所示。

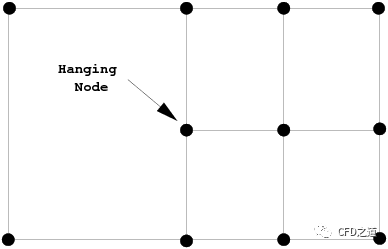
悬挂节点自适应方法使用一些预定义模板来递归地细化网格中的单元，该方法可以细化三角形、四边形、四面体、六面体、棱柱网格和金字塔网格，但无法细化多面体。此方法需要额外的内存来维护网格细化级别的层次结构，在将网格恢复到原始网格的网格粗化过程需要这种层次结构数据。

标记为细化的网格按如下所述方法进行剖分：

• 1个三角形网格被分割成4个三角形网格
• 1个四边形网格被分割成4个四边形网格

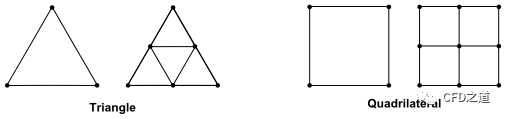
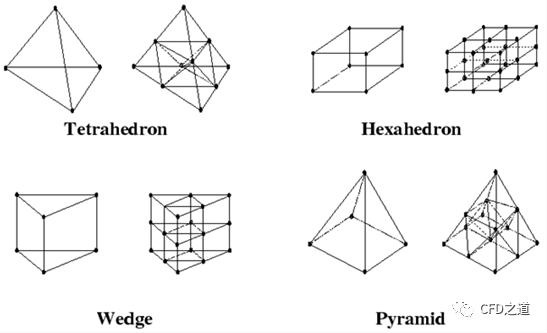
• 1个四面体网格被分割成8个四面体网格
• 1个六面体网格被分割成8个六面体网格
• 1个三棱柱网格被分割成8个三棱柱网格
• 1个金字塔网格被分割成6个金字塔网格与4个四面体网格

为了保证计算精度，相邻的单元格之间的差异不允许超过一个细化级别（refine level），这可以防止产生过多的网格单元体积变化(减少截断误差)，并确保父网格单元(原始网格)和子细胞(细化的网格)的网格中心位置接近(减少通量计算中的误差)。

细化后的网格可以通过重新引入未激活的母网格（合并子网格以重新获取之前被细分的母网格）而重新粗化。若一个未激活的母网格的所有子网格都被标记为粗化时该母单元会被重新激活，软件最终可以恢复到原始网格。因此，此方法粗化后的网格无法比初始网格更粗。

悬挂节点方法存在以下限制：

• 无法处理多面体网格
• 与动网格方法中的dynamic layering及remeshing方法不兼容，无法一起使用
• 面和/或网格区域分离应在悬挂节点适应之前进行，否则需要将包含悬挂节点的网格转换为多面体网格
• 不支持各向异性网格适应

1.2 多面体非结构网格自适应

多面非结构网格自适应(PUMA)方法只适用于三维网格，该方法为默认选项。PUMA将自适应技术推广到含有任意多面体的网格，其不依赖于模板进行细化，故该方法不局限于特定的网格类型，可以用于细化任何3D网格类型(如多面体、四面体、六面体等等)。与悬挂节点方法相比，此方法在网格适应过程中消耗的内存更少。

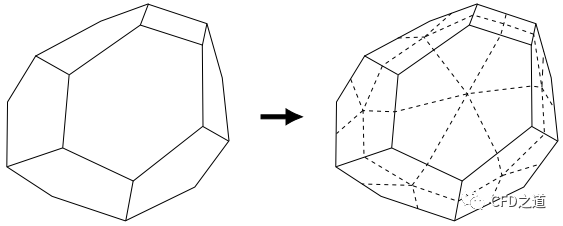
网格细化后还能被粗化，不过只有当母网格中的所有子网格都被标记为粗化时才可以恢复。基于此方法，粗化的网格尺寸不可能比原始网格大。

PUMA方法存在以下一些限制：

• 仅用于3D网格
• 非凸多面体无法保证被细化，如果无法产生具有正体积和可接受正交质量的子网格，则细化过程会被跳过
• 自适应网格中可能会包括多面体网格，然而多面体网格与动网格中的dynamic layering及remeshing方法不兼容。不过如果区域中没有多面体网格的话，则可以使用
• 如果选择将case文件写入legacy格式(cas与dat格式文件)，则不支持将网格适应层次结构及网格细化历史写入文件。这意味着以传统格式保存的数据文件被重新读入后，网格是无法粗化的
• PUMA方法不能应用于具有层次结构的网格(如hexcore类型的网格)，不过可以使用mesh/polyhedra/convert-hanging-nodes文本命令将网格转换为多面体从而删除网格层次结构

2 各向异性网格适应

各向异性玩个适应的目的是在三维网格中细化六面体或棱柱层网格单元。该方法被认为是一种网格操作工具，而不是一种网格适应特性，其允许使用GUI细化与一个或几个边界面区域相邻的六面体或棱柱单元，六面体或棱柱网格每次在一个方向上分裂，用户可以控制不同的分裂比例，从而实现各向异性网格细化。

注：各向异性网格适应只能进行网格细化，无法进行粗化。

3 基于几何的自适应

网格自适应的目的是产生一套足够精细和充分代表所有重要的几何特征的网格。然而当用户有一个粗糙的几何网格，如有弯曲的轮廓和尖锐的角度，适应的网格可能无法与曲线轮廓和角落周边的几何相匹配。在这种情况下，可以使用基于几何的网格适应来重建几何(或恢复几何更精细的细节)。

基于几何的自适应基于几何重构原理。在这种方法中，通过在网格的现有节点之间的域中创建新的节点来增加网格单元数量。新创建的节点投影到原始几何上，这样得到的网格更精细，形状更接近原始几何形状。

考虑一个为圆形几何创建的粗网格（图5左）。网格靠近圆形边缘的部分如左图所示，网格边缘不光滑且存在尖锐棱角，网格形状与原几何形状不太相似。使用边界适应和几何重建将得到一个边缘更平滑的网格，如右图所示。

在右图中，虚线为网格的原始边缘。边界适应过程在原始节点之间创建新的节点，这些节点被投影到几何图形的边缘，因此得到的网格具有光滑的边缘，其形状更接近原始几何图形。

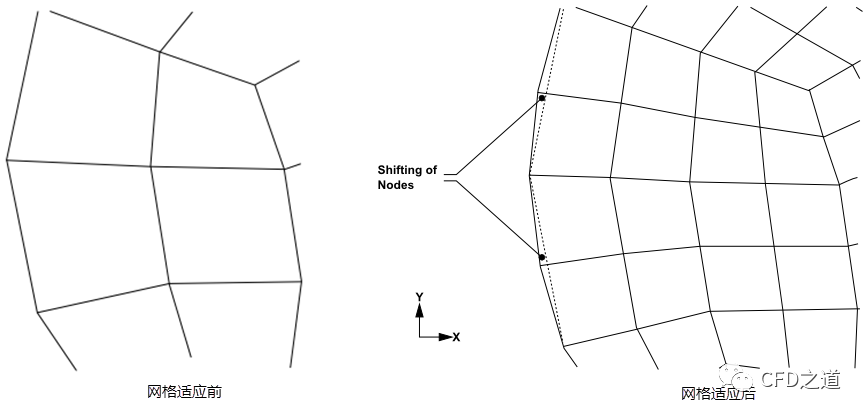
注意：只有在网格适应过程中创建的网格节点(新创建的节点)才会被投影，原始网格节点将保留它们的位置步兵。

节点投影包含众多控制参数，包括：

• Levels of Projection Propagation：此参数允许指定用于几何重构的节点传播跨越的节点层数。值1表示只投影边界上的节点，值2表示投影边界上的节点和下一层的节点，依此类推，如下图所示

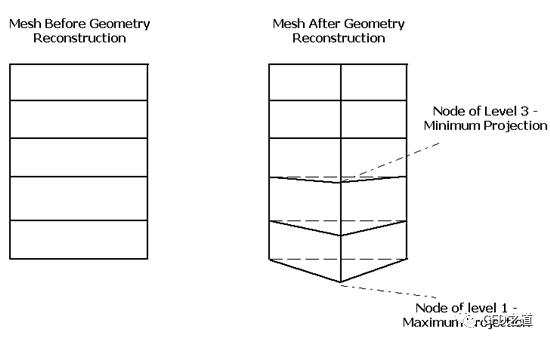
• Direction of Projection：该参数允许为节点投影指定方向，X、Y或Z(对于3D)。如果不指定任何方向，则节点投影将发生在新创建节点的最近点。
• Background Mesh：这个选项允许你使用一个精细的表面网格作为背景网格，然后用来重建几何图形。读取表面网格时，将根据背景网格的节点位置进行节点投影

（未完待续）