本文描述Fluent中Critical Heat Flux壁面沸腾模型的基础理论。

注：内容取自Fluent Theory Guide。

在壁面沸腾时，临界热流密度(Critical Heat Flux，CHF)条件的特征为局部换热系数急剧减小，且壁面温度偏移。当加热的壁面随蒸汽含量的增加而不再被沸腾的液体浸湿时，就会发生这种现象。在临界热流条件下，蒸汽取代液相占据了加热壁面附近的空间，热量能够直接从壁面转移到蒸汽中，进而导致散热能力迅速下降，蒸汽温度急剧上升。此外，壁面沸腾与成核沸腾分离，多相流由泡状流转变为雾状流。

为了模拟临界热流条件，Fluent将RPI模型从核状沸腾状态扩展到临界热流及干态沸腾，同时考虑以下因素：

• 广义非平衡壁面热流分配
• 流型由泡状向雾状过渡

1 壁面热流分配

壁面热流分配采用与非平衡过冷沸腾模型方程相同的形式。

这里函数取值范围0~1。

Lavieville et al^[1]提出下面的计算方式：

式中，临界液相体积分数为，对于汽相临界体积分数。

Tentner et al.^[2]基于汽相体积分数提出下面的计算方式：

在Fluent中，此式为壁面热流分配的默认计算方式。

Ioilev et al.^[3]在壁面热流分配中考虑薄膜沸腾，利用线性函数将上式扩展到临界热流条件：

式中，断点被设置为。

2 流型转换

当壁面沸腾脱离成核沸腾状态，达到临界热流及干态条件时，多相流由泡状流转变为雾状流。相应的在泡状流动状态下，液相由连续相转变为分散相，而汽相由原来的分散相转变为连续相。随着流态的转变，界面面积、动量传递项(阻力、升力、湍流分散、界面面积等)、传热和湍流量也会发生相应的变化。

为了模拟流型的变化并计算界面传递，传统上采用基于界面平均流动参数的流型图来考虑。在CFD求解器中，流型图的概念被扩展到局部基于网格单元界面表面拓扑结构，从而利用局部流动参数来考虑流态转换。所有计算单元通常具有简单的局部界面表面拓扑，可以提供复杂的全局拓扑来表示与传统子通道流型图不同的流型。

首先，采用简单的局部界面表面拓扑来控制连续液相泡状流到连续汽相液滴流态平稳过渡^[4]。它假设在一个计算单元内，局部界面表面拓扑包含多个连接的界面，且流态由单个局部流动变量汽相体积分数决定：

• 泡状流（Bubbly flow）：汽相以气泡的形式分散在连续的液体中，通常
• 雾状流（Mist flow）：液相以液滴的形式分散在连续的蒸汽中，通常
• 混状流（Churn flow）：介于泡状流与雾状流之间的流型，通常

利用界面表面拓扑来计算界面面积和界面动量和热量的传递。引入表示界面量(界面面积、阻力、升力、湍流漂移力和传热)，然后用下面的通用形式计算：

式中，通过壁面热流分配公式进行计算，参数及分别为泡状流及雾状流的界面量，取值为0.3及0.7。

需要注意在沸腾模型中，通常定义液相为主相，而蒸汽相被定义为次相。一旦这样定义后，其不会随着流型转变而发生改变。当参数及计算完毕后，主相与次相被互换。对于，液相被当做主相而蒸汽相为次相；对于，蒸汽相被作为主相而液相为次相。

3 相间动量传递

相间动量传递可能包括五个部分：阻力、升力、壁面润滑力、湍流漂移力和虚质量力等。每种效应都有不同的模型，其中一些模型是专门为沸腾流动设计的。此外也可以使用UDF进行定义。

3.1 界面面积

界面面积（Interfacial Area）可利用用输运方程或界面面积浓度所描述的代数模型来计算。对于沸腾流动，一般选用代数模型（参见18.5.5）。

从球形气泡或液滴的表面积与体积之比出发，推导出代数界面面积浓度模型：

式中为气泡或液滴的直径。Eulerian多相流模型中可用的袋鼠模型包括：

• Particle model (默认)

对于体积分数的分散相，Particle模型采用下式估算相间界面面积密度:

• Symmetric model

symmetry模型认为相p与相q为对称（p与q可用为连续相或分散相），相间界面面积密度可通过下式计算：

其中，分别为相p与相q的体积分数。为特征长度，可通过下面的方式计算：

若相p为分散相：

若相p与相q均为分散相：

• Ishii model（仅用于沸腾流动）

只有在沸腾模型被激活时，Ishiii模型才可用，该模型对Particle模型进行了修改，结果是一个与相关的分段线性函数，当接近1时，函数值接近0。

在Fluent中，参数取值0.25。

• Gradient model

梯度模型与对称模型的不同之处在于，它将相界面处的梯度作为界面长度尺度引入。若连续相p与分散相q之间存在自由界面，则相间界面密度计算为：

若相p与q均为分散相，则相间界面密度计算为：

• UDF

可以使用UDF宏DEFINE_EXCHANGE_PROPERTY对相间界面密度进行定义。

3.2 气泡或液滴的直径

1、气泡直径

默认情况下，Fluent将气泡直径考虑为局部过冷度的函数。

局部过冷度：

气泡直径的计算方式为：

式中，

也可以使用Unal^[5]提出的气泡直径计算方法：

若想要使用Unal方法，需要在TUI窗框使用命令：

(rpsetvar 'mp/boiling/bubble-diameter-model 1)

2、液滴直径

当流型转换为雾状流时，假设液滴直径为常数，并通过Kataoka-Ishii^[6]提出的关系式进行计算：

式中，；为汽相体积通量（表观速度）；为液相局部雷诺数；为汽相局部雷诺数；为液相粘度；为汽相粘度。

3.3 相间曳力

Fluent提供了很多种计算分散相曳力的方法（如Schiller and Naumann Model、Morsi and Alexander Model、Symmetric Model、Grace et al. Model、Tomiyama et al. Model、Ishii Model、Ishii-Zuber Drag Model、Universal Drag Laws等）。沸腾流动一般推荐选用Ishii Model。当然也可以选择使用Fluid-Fluid Exchange Coefficient 中列出的其他模型。

在沸腾流动中可以使用Ishii模型^[7]考虑相间曳力。Ishii模型通过选取阻力系数在粘性状态和畸变状态下的最小值来确定，定义如下：

5^[8]: 5 M. Ishii. “Two-fluid model for two-phase flow”. 2nd International Workshop on Two-phase Flow Fundamentals. RPI, Troy, NY. 1979.

式中，和通过下式进行计算：

式中，Re为相对雷诺数；为表面张力系数；为重力加速度。

3.4 相间升力

ANSYS Fluent提供了多种模型来计算分散相上的升力（包括Moraga Lift Force Model、Saffman-Mei Lift Force Model、Legendre-Magnaudet Lift Force Model、Tomiyama Lift Force Model等）。对于沸腾流动，升力在成核沸腾过程中很重要。在RPI模型中，通常选择Tomiyama Lift Force Model来考虑界面升力的影响。

Tomiyama升力模型适用于较大规模的可变形气泡在椭球和球帽状态时的升力计算。该模型依赖于Eotvos数，其的主要特点是预测气泡大小的交叉点（在这个交叉点上颗粒形状畸变导致其升力方向发生改变）。

在Fluent中实现的模型是Frank等人(2004)^[9]对标准Tomiyama升力模型(1998)^[10]的一个修正版本。

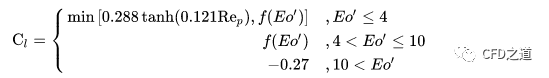
式中，

为基于变形气泡长轴的修正Eotvos数：

式中，为表面张力系数，为重力加速度，为气泡直径。

3.5 湍流分散力

Fluent提供了多种计算湍流分散力的模型（Lopez de Bertodano Model、Simonin Model、Burns et al. Model、Diffusion in VOF Model等）。在沸腾流动中，湍流分散力将蒸汽从壁面输送到核心流体流动区域。在RPI模型中，建议选择Lopez de Bertodano模型来考虑湍流色散力的影响。

Lopez de Bertodano^[11]模型采用下面的方式计算湍流分散力：

式中，为连续相的密度；为连续相的湍动能；为分散相体积分数梯度；为用户修正常数，取值为1。

3.6 壁面润滑力

壁面润滑力在成核沸腾状态下较为重要。Fluent提供了一些模型用于考虑壁面润滑力，这些模型包括Antal et al. Model、Tomiyama Model、Frank Model、Hosokawa Model等。在RPI模型中，通常推荐使用Antal et al. Model考虑壁面润滑力。

壁面润滑力采用下面的方式进行计算：

式中，为壁面润滑力系数；为主相密度；为次相体积分数；为相相对速度沿壁面切向分量；为壁面向外的法向方向向量。

Antal et al.^[12]模型指定壁面润滑力系数为：

式中，，，为气泡/颗粒直径，为近壁面距离。

注意系数仅当非常临近壁面时才为非零值：

参数及默认值对应着，因此，Antal模型需要足够细密的计算网格。

3.7 虚质量力

在多相流中，当次相p相对于主相q加速时存在虚拟质量效应。虚质量力定义为：

式中，为虚质量系数，通常取值0.5；项表示q相的物质导数：

虚质量力附加在动量方程的右侧。

4 相间传热

4.1 界面液相传热

当气泡离开壁面并向过冷区移动时，会存在从气泡到液相的传热，定义为：

式中，为换热系数。换热系数可以通过Ranz-Marshall或Tomiyama模型计算得到。

相p与相q之间的换热系数计算采用下式：

其中，为液相的热导率，为气泡直径。因此换热系数的计算集中在Nu数的处理上。

Ranz and Marshall^[13]利用下式计算Nu数：

式中，为基于s相粒径以及相对速度的相对雷诺数；为l相的Prandtl数，其定义为：

Tomiyama^[14]模型对界面换热提出了一种略有不同的关系式，适用于雷诺数较低的湍流泡状流动，其计算Nu数的方法为：

4.2 界面汽相传热

界面汽相传热采用constant time scale return to saturation method^[15]方法计算，该方法假设蒸汽通过快速蒸发/冷凝来保持饱和温度。公式为：

式中，为时间尺度，默认值0.05；为等压比热容。

5 质量传递

5.1 壁面向蒸汽相传质

蒸发质量流量作用于容器壁面附近的网格单元，它是由蒸发热通量导出的：

5.2 相间传质

相间界面传质直接取决于相间界面传热。假设所有传递到界面的热量都用于传质(即蒸发或冷凝)，则界面传质速率可表示为

6 湍流作用

在模拟沸腾流动时，通常加入湍流相互作用模型来描述附加的气泡搅拌和耗散。沸腾流动有三种选择:Troshko-Hassan(默认值)、Simonin等和Sato。

参考文献