本文描述Fluent中蒸发-冷凝模型所涉及到的基础理论。

注：以下内容来自Fluent Theory Guide。

Fluent中提供了两种模型来考虑涉及到蒸发-冷凝的多相传质过程。在VOF及Mixture多相流模型中，可以使用Lee模型，在Eulerian模型中，可以使用Lee模型及Thermal Phase Change模型。

1 Lee Model

Lee模型是一个基于物理基础的力学模型，该模型常用于Mixture模型及VOF模型，如果使用整体界面传热系数模型（不采用双热阻模型）的话，也可以在Eulerian模型中选用。

在Lee模型中，液-汽传质(蒸发和凝结)由汽相输运方程控制：

式中，为汽相；为汽相体积分数；为汽相密度；为汽相速度；分别为蒸发及冷凝的质量传递率，单位kg/s/m3。

如方程中所示，Fluent将冷凝（汽相转化为液相）传质率定义为负值，而将蒸发传质率定义为正值。

蒸发与冷凝的传质率通过饱和温度来计算。

当时（蒸发过程）：

当时（冷凝过程）：

式中，参数coeff为一个调整系数，可以解释为弛豫时间的倒数（单位1/s）。及分别为相体积分数以及密度。能量方程源项可以通过传质率与潜热的乘积计算得到。

考虑Hertz Knudsen公式，该公式基于平板界面的动力学理论给出了蒸发-凝结通量：

通量单位为kg/s/m2。式中，为压力，为温度，为普适气体常数。系数为所谓的调节系数，其表示进入液体表面并被液体表面吸收的蒸汽分子的比例。表示蒸汽侧界面处的蒸汽分压。通过克拉珀龙-克劳修斯（Clapeyron-Clausius）方程将饱和条件下的压力与温度联系起来（由蒸汽化学势和液体化学势相等得到的）：

式中，及分别为蒸汽相与液相密度的倒数（单位质量的体积）；为潜热（J/kg）。

根据这个微分表达式，我们可以从接近饱和状态的压力变化得到温度变化。

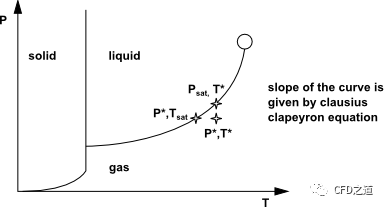
只要与接近饱和条件，利用克劳修斯-克拉珀龙方程就可得到以下公式：

利用上面的Hertz Knudsen方程可以得到：

式中因子通过调节系数和蒸汽的物理特性来定义，其在平衡条件下近似为1.0。

在Eulerian及Mixture多相流模型中，假定流态是分散的。如果假设所有的蒸汽相以气泡形式存在，且气泡具有相同的直径，则界面面积密度（Interfacial area density）可通过下式计算得到：

式中，为气泡粒径，m。

因此可得到相源项：

与前面的传质率公式进行比较，可以得到调节系数coeff的计算公式：

这就得出了前面方程中定义的蒸发过程的最终表达式，其可以隐式地作为相守恒方程中的一个源项。

冷凝过程与之类似，此时考虑的是连续汽相中的小液滴。

需要注意，对于蒸发与冷凝过程，系数coeff理论上应该是不同的，且理论表达式基于以下几个假设：

• 平的相间界面
• 等直径的分散相体系
• 参数已知

气泡直径和调节系数在计算之前通常都是未知值，这就是为什么必须对系数coeff进行微调以匹配实验数据的原因。 默认情况下，蒸发和凝结的系数都是0.1。然而，在实际情况中，系数coeff的数量级可能高达1000。

2 Thermal Phase Change Model

当采用欧拉多相模型及双热阻法（ two-resistance approach）计算相间传热系数时，热相变模型（thermal phase change model ）可用于蒸发-冷凝模拟。

在双热阻法计算相间换热系数时，液相界面的换热量与汽相侧的换热量可分别通过下面的公式进行计算 。

• 对于液相界面换热量

• 对于蒸汽相界面换热量

式中，及分别为液相与汽相的换热系数；及分别为液相及汽相的焓；及为缩放因子，默认情况下及取值为1；界面温度通过热力学平衡决定，当忽略表面张力对压力的影响时，可以假设，此处为饱和温度。

由于热和质量都不能储存在相界面上，因此必须满足整体热平衡：

由上述方程，通过蒸发从液体到气相的传质可以表示为：

两相焓值及需要正确计算，以考虑由于两相之间的潜热以及两相之间的热传递而导致的静焓值的不连续性。使用Prakash公式，主流流体的焓从输出相中得到，饱和焓从输入相中得到。

当时（蒸发，液相为输出相）：

当时（冷凝，液相为输入相）：

这样能确保传质计算公式的分母不为零。

潜热可通过下式进行计算：

可以看出，当存在传质时，和为总相焓，可写成通用形式：

其中，为参考温度；为温度下的标准状态焓，每一相的焓表达形式都相同。

在热相变模型中，蒸发-冷凝传质过程完全由相间传热过程和整体热量平衡控制，不再需要校准如Lee模型中存在的传质系数，因此，在模拟蒸发-冷凝过程时，一般建议使用欧拉多相流模型，并采用双热阻传热法。