本文介绍Fluent凝固熔化模型中所涉及的基本理论。

1 模型简介

ANSYS Fluent可以用来求解涉及到包括在一个温度(如纯金属中)或某个温度范围(如在二元合金中)下发生的凝固和/或熔化问题。在此类问题的处理中，Fluent不显式跟踪液固界面，而是采用焓-孔隙率公式进行计算。通过将液固糊状区视为多孔介质，并将液相体积分数等效为孔隙率，在动量方程中加入适当的源项来处理由于固体材料的存在而产生的额外压力降。

Fluent中提供了以下能力模拟凝固熔化过程：

• 纯金属和二元合金的液-固凝固/熔化的计算
• 连铸过程的建模
• 固化材料与墙体之间的接触热阻建模(如由于空气间隙的存在)
• 凝固/熔化过程中组分输运的建模
• 与凝固/熔化相关的物理量的后处理(如液相体积分数和拉出速度)

这些建模能力允许Fluent模拟大范围的凝固/熔化问题，包括熔化、凝固、结晶生长和连铸等。

2 局限性

Fluent中的凝固/熔化模型存在以下使用限制：

• 凝固/熔化模型只能与压力基求解器一起使用，在密度基求解器中不可使用
• 凝固/熔化模型不能用于可压缩流动
• 常规的多相流模型（VOF、Mixture、Eulerian模型）中，只有VOF模型可以和凝固/熔化模型一起使用
• 除了组分扩散率，用户无法通过GUI为固体和液体材料指定单独的材料属性。但是可以使用DEFINE_PROPERTY宏来指定固体和液体的属性。
• 在凝固/熔化模型与存在化学反应的组分输运模型一起使用时，无法将化学反应限制在液相区域内，实际上在所有区域都会求解化学反应

3 介绍

在Fluent中采用焓-孔隙率（enthalpy-porosity）技术对凝固/熔解过程进行建模。在这种技术中，不显式跟踪熔体界面，而是采用一个称之为液相分数（liquid fraction）的物理量来表达，在每次迭代计算中，根据焓平衡来介绍液相分数。

糊状区是液体分数在0和1之间的区域。将糊状区模拟成“伪”多孔介质，随着材料的固化，孔隙率从1降低到0。当材料完全凝固时，孔隙率变为零，速度也降为零。

4 能量方程

材料的焓计算为显焓与潜热之和。

式中：

其中，为参考焓；为参考温度；为定压比热容。

液相分数定义为：

潜热量可写成液相潜热值与液相分数的乘积：

潜热量变化范围为0（为固体）到（为液体）。

对于凝固熔化问题，其能量方程可写为：

式中，

为焓，为密度，为流体速度，为源项。

直接利用液相分数方程计算液相分数会导致能量方程难以收敛。在Fluent中，使用Voller和Swaminathan提出的方法更新液相分数。对于纯金属，其，则使用Voller和Prakash给出的基于比热的方法来更新液相分数。

5 动量方程

焓-孔隙率技术将糊状区域(部分凝固区域)视为多孔介质。单元的孔隙率等于该单元中的液相分数。在完全凝固区域，孔隙率及流动速度均为零。由于糊状区孔隙率降低而引起的动量衰减可表达为以下形式：

式中，为液相体积分数，为一个防止分母为零的极小值（0.001），为糊状区常数，为拉出速度。

糊状区常数用于控制材料凝固时速度变化量，该值越大，材料凝固时速度降低得越快。该常数取值非常大时可能会导致求解振荡。

在连铸过程中，拉出速度被考虑为凝固材料的运动，因为它在连铸过程中不断地从区域中被拉出。方程中的这一项允许新凝固的材料以拉出速度运动。如果固化材料没有从区域中被拉出，。

6 湍流方程

在糊状区与凝固区的湍流方程上添加源项，以描述固体物质的存在。源项形式与动量方程源项相似：

式中，为湍流物理量（如湍动能、湍流耗散率等），为糊状区常数。

7 组分方程

对于纯净物质的凝固及熔化，相变发生在不同的熔化温度下；而对于多组分混合物，在较低的固相线与较高的液相线温度之间存在糊状的凝固/熔化区。当多组分液体凝固时，溶质从固相扩散到液相，这种效应可以利用溶质的组成系数来量化，其描述为界面处固相质量分数与液相质量分数的比值。

Fluent采用以下方式计算多组分混合物的固相线温度和液相线温度。

固相线温度：

液相线温度：

式中，为溶质的组成系数；为溶质的质量分数；为液相线的斜率。

如果质量分数的值超过共晶质量分数的值，则在计算液相线和固相线温度时将其截断。计算时假设混合物的最后一种组分为溶剂，其他组分为溶质。

Fluent预计用户将为组分的液相线输入一个负斜率。如果用户输入一个正的斜率，Fluent会忽略该输入，转而使用共晶温度和共晶质量分数来计算斜率：

在多组分混合物中，通过常规的液相分数方程更新液体分数会导致数值误差和收敛困难。此时采用以下迭代方程计算液相分数：

式中，上标表示迭代次数；为松弛因子，默认值为0.9；为单元矩阵系数；为时间步长；为当前密度；为网格单元体积；为当前网格的温度；为界面温度。

Fluent提供了两种微观尺度上的组分分离模型，即Lever法和Scheil法。前者假定溶质在固体中无限扩散，而后者假定溶质无扩散。对于Level法，界面温度采用下式进行计算：

式中为组分的数量。

而Scheil法采用下式计算。

利用Lever法的组分输运方程可表述为：

式中，为反应速率；表述为：

其中，为液相速度；为固相速度（拉出速度），当求解中不包含拉出速度时，该变量为零。液相速度可以通过下式计算：

液相（）及固相（）质量分数由分配系数相联系：

当使用Scheil模型时，Fluent通过求解以下方程获取：

8 反扩散

Scheil法假设固体区域内溶质扩散为零，而Lever法则假设固体区域内溶质扩散为无穷大。反扩散模型在微观水平上使用一个无量纲参数在0(在Scheil规则中没有扩散)与1(在Lever规则中无限扩散)之间建立有限固体扩散的微观模型。取决于凝固条件，如固体扩散系数、局部凝固时间和二次枝晶臂间距等。界面温度通过下式计算：

当Scheil法包含反扩散时，组分扩散方程表示为：

总组分质量分数与液体组分质量分数关系为：

9 连续铸造中的拉出速度

在连铸过程中，凝固物质通常是连续地从计算域中被拉出，如下图所示。因此固体材料的速度是有限的，必须在焓-孔隙度模型中加以考虑。

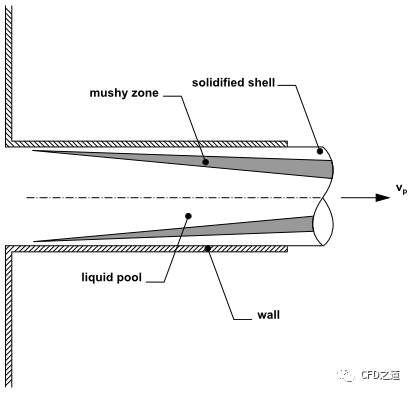
如动量方程所述，焓-孔隙度方法将固-液糊状区视为多孔介质，孔隙度等于液体分数。在动量方程中加入一个合适的源项来考虑由于糊状带的多孔结构而引起的压降。对于连铸应用，动量方程源项使用液体与固体之间当相对速度，而非绝对速度。

固体拉出速度的精确计算取决于固体的杨氏模量、泊松比以及作用于其上的力。Fluent基于凝固区域边界处的速度，利用拉普拉斯方程来近似固体区域的拉出速度：

Fluent在计算拉出速度时采用了以下边界条件：

• 在速度入口、静止壁面或移动壁面上，使用指定的速度
• 在所有其他边界(包括液-固界面)，使用零梯度速度。

仅在固体区域中计算拉出速度。请注意，Fluent可以制定拉出速度为指定的常数值或自定义的场函数。

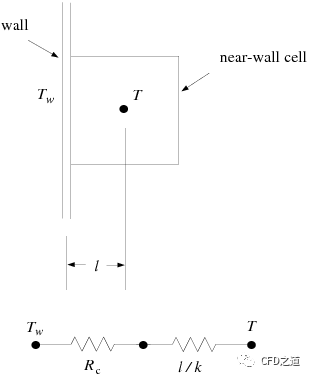
10 壁面接触热阻

Fluent s凝固/熔化模型可以利用壁面与液相分数小于1的网格单元之间当额外热阻来考虑壁面与凝固材料之间存在的空气间隙。这种接触热阻是通过改变近壁流体的热导率来考虑的。因此，壁面热通量可表示为：

式中，及如下图所示。为流体热导率；为液体体积分数；为接触热阻。

11热浮力与溶质浮力

在涉及到多组分多凝固/熔化过程中，液池密度随温度和组分的变化而变化。在重力场存在的情况下，浮力将由两种机制引起：

• 热浮力（Thermal buoyancy）：密度随温度改变而以引起当浮力
• 溶质浮力（Solutal buoyancy）：密度随熔体物质组成变化而引起的浮力。在多组分凝固问题中，溶质在液固界面附近不断被排斥，导致液池中溶质富集。这种对溶质的富集使固液界面附近产生浓度梯度，从而产生密度梯度。

热浮力与溶质浮力模型的建立对于准确预测整体凝固行为具有重要意义。由于热浮的作用，流动趋向于促进混合和平滑温度梯度。因此，排除这一项会导致对凝固时间的预测不准确。Solutal浮力将富集液体移离液-固界面，并将其替换为远场标称成分液体，排除Solutal浮力会导致对多组分材料偏析模式的过度预测。

针对多组分凝固问题，Fluent采用Boussinesq方法建立浮力诱导流动模型。热浮力按自然对流和浮力驱动流动理论计算。由Solutal浮力引起的体积力是用类似的方法计算的：

式中，为液相中溶质的质量分数；为组分的参考质量分数；为组分的膨胀系数；为溶质组分的数量；为重力加速度向量；为参考密度。

总体力是热浮力和溶质浮力之和，二者具有相似或相反的符号。

注：本文内容来自Fluent Theory Guide。