本文通过案例描述边界类型之间的相互关系。

1 案例描述

尽可能简单的案例。考虑一个长度100 mm，直径20 mm的圆管，入口速度1 m/s，流体介质为液态水（密度1000 kg/m3，动力粘度0.001 Pa.s)。

雷诺数：

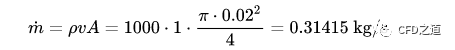
采用SST k-omega湍流模型进行计算。计算中采用2D轴对称模型，计算模型如图所示。

2 计算过程

以下计算过程均未设置压力出口的指定流量。

2.1 速度入口压力出口

采用入口速度1 m/s，出口静压0 Pa进行计算。

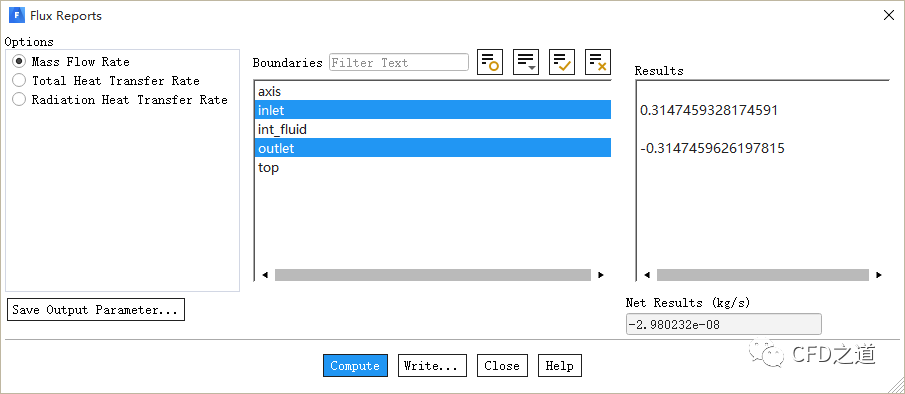
计算完毕后统计出口流量，如下图所示。

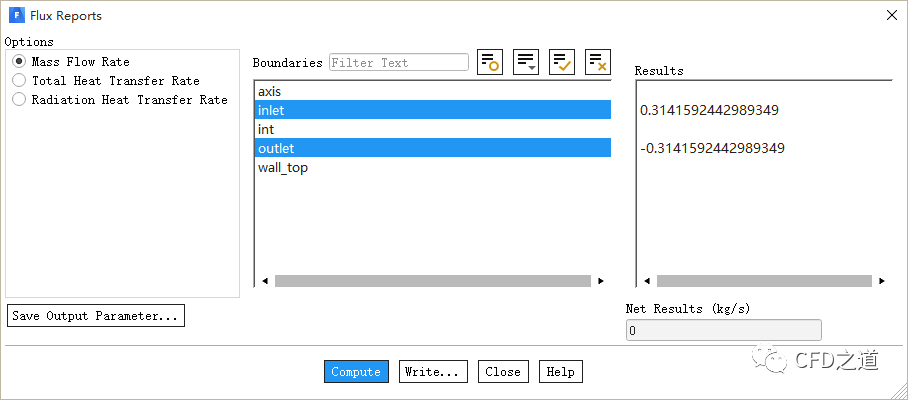
这没有太大问题，出口流量：

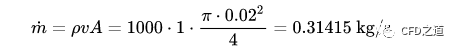
再看一下进出口总压。

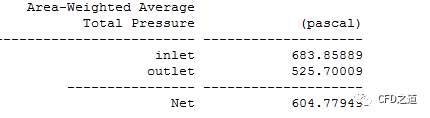
进出口静压如图所示。

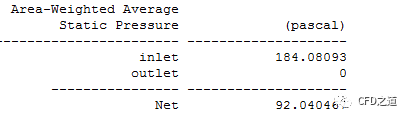
下一步将总压683.85889 Pa作为压力入口，出口压力依然为静压0 Pa，计算进出口流量。

2.2 压力入口压力出口

入口总压683.85889 Pa，出口静压0 Pa。

计算完毕后统计总压与静压。总压数据如下图所示。

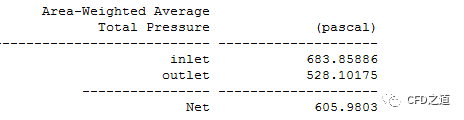
静压数据如下图所示。

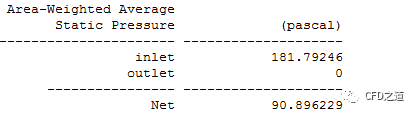
流量数据如图所示。

速度如图所示。

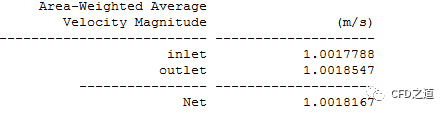
流量有偏差，下面用流量入口压力出口试试。

2.3 流量入口压力出口

入口流量0.314159 kg/s，出口静压力0 Pa。

流量入口压力出口收敛极慢，但能够保证进出口流量一致。

速度数据：

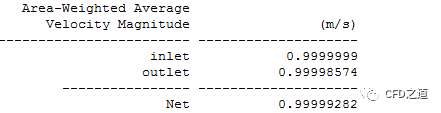
静压数据：

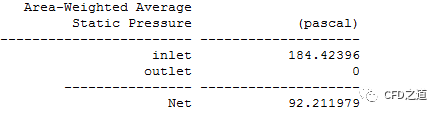
总压数据：

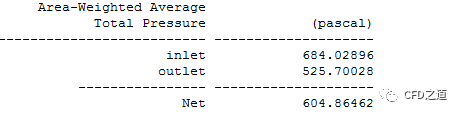
2.4 出口静压100 Pa

采用入口速度1 m/s，出口静压100 Pa，看看计算结果。

速度数据：

静压数据：

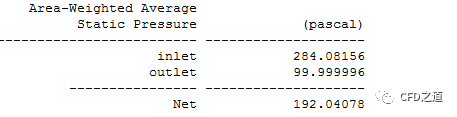
总压数据：

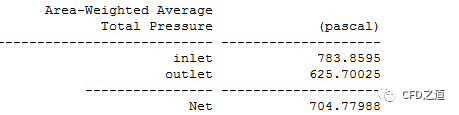
3 数据分析

分别用速度入口、压力入口以及流量入口进行计算，出口均设置为静压0 Pa，计算结果如表所示。

	速度入口	压力入口	流量入口
入口速度	1	1.001779	0.999
入口静压	184.080	181.792	184.42
入口总压	683.858	683.85	684.02
入口流量	0.31415	0.3147	0.3141
收敛情况	78步收敛到1e-4	324步收敛到1e-3	1000步未收敛到1e-3

从数据上看，基本上可以认为三种边界组合的计算结果是等效的，存在的差异可以认为是计算误差。然而收敛状况差异很大，计算的收敛状态与常规建议倒是比较吻合，不可压缩流动个计算，速度+压力是最推荐的组合，不建议使用流量+压力，压力+压力可以用，但是也并不推荐。

来分析表格中的数据。

可以很容易发现，入口总压是等于入口静压加上入口动压的。在入口速度1 m/s，流体密度1000 kg/m3的情况下，入口动压为500 Pa。

所以经常有人问使用压力入口时如何保证流量，嘿，你得自己将流量换算成速度换算成动压然后再加到静压上去，这样才能保证入口速度和入口流量。

对比入口速度均为0，出口压力为0 Pa与出口压力为100 Pa时的计算结果，如下表所示。

	出口静压0 Pa	出口静压100 Pa
入口静压	184.08093	284.08156
入口总压	683.85889	783.8595
出口总压	525.70009	625.7002
入口速度	1	0.99999

看出规律了么？出口静压对其他压力（入口静压、入口总压、出口总压）的影响是线性叠加的，就是赤果果的往上代数相加，毫无技术含量可言。其实很容易解释，流体的沿程损失与流量相关，当流量保持不变时，其沿程损失也不变。

---

这次比较的是不可压缩，流体遵循伯努利方程。当流体可压缩时，问题会变得稍微复杂一些，这次就懒得去讨论了，有兴趣的道友自行摸索吧。

健康码都绿了还不让出门，再不找Tony老师的话，都要没脸见人了！

本篇文章来源于微信公众号: CFD之道