本文描述CFD中一些常见的无量纲数。

注：

注：本文内容译自《The finite volume method in computational fluid dynamics _ an advanced introduction with OpenFOAM® and Matlab》，Darwish, M. Mangani, L. Moukalled, F

”

1 Reynold数

雷诺数^[1]定义为:

式中，为流体密度；为流动速度；为特征长度；为动力粘度。

雷诺数表示为流体对流(惯性)与扩散(粘滞)动量通量的相对重要性。则如图所示，雷诺数可用于表征流动状态(层流、过渡流或湍流)。

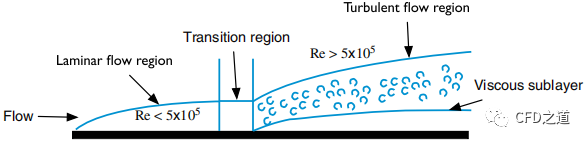
2 Grashof数

格拉晓夫数定义为：

式中，为重力加速度；为热膨胀系数；为温差；为特征长度；为运动粘度。

格拉晓夫数表示浮力与粘性力之比。该参数在自然对流中起着与雷诺数在强制对流中同样的作用。下图中描述了一个Grashof数影响的示例。

3 Prandtl数

普朗特数定义为动量扩散与热扩散的比值：

式中，为动力粘度；为等压比热容；为热导率；为运动粘度；为热扩散系数，。

Pr>1，热边界层在流动边界层内部；Pr<1，热边界层在流动边界层外部；Pr=1，热边界层与流动边界层重合。

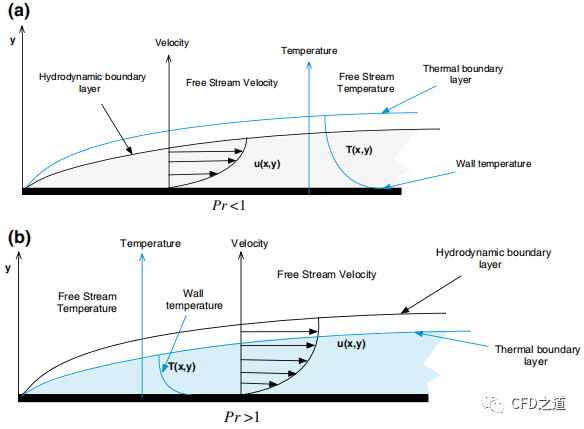
4 Peclet数

Peclet数^[2]定义为物理量的对流输运速率与扩散输运速率之比。

对于涉及传热的问题，Peclet数定义为：

此时，Peclet数为雷诺数与普朗特数的乘积。

对于质量输运问题，Peclet数定义为：

式中，为质量扩散率，为Schmidt数，此时Peclet数等于雷诺数与Schmidt数的乘积。

较大的Peclet数表明流动对下游位置的依赖性较低，对上游位置的依赖性较高。因此对于Peclet数较高的情况，可以采用较为简单的计算模型进行模拟，如CFD中广泛采用的迎风格式非常适合于大Peclet数条件下。

5 Schmidt数

施密特数^[3]定义为：

式中，为运动粘度；为质量扩散率。

传质中的施密特数与传热中的普朗特数类似，其表示动量扩散率()与质量扩散率()的比值。

6 Nusselt数

努塞尔数^[4]定义为：

式中，为对流换热系数；为热导率；L为特征长度。

7 Mach数

马赫数^[5]定义为运动速度与当地声速的比值：

式中，为流体的速度值；为声速。

声速可通过下式进行计算：

对于理想气体，声速计算方式可表示为：

式中，为绝热指数，定压比热容与定容比热容的比值；为普适气体常数。

当马赫数小于0.2通常认为流体不可压缩；M<1为亚音速，M=1为音速，15为高超音速。从亚音速加速到超音速的流动称为跨音速流动。

8 Echert数

埃克特数^[6]表示流动动能与边界层焓差之间的关系，用于表征散热。

式中，为特征温差。

大的埃克特数表示高粘性耗散，对于小的埃克特数（），可以忽略能量方程中的一些项（如粘性耗散，体积力等）。

9 Froude数

弗劳德数^[7]（Fr）表征惯性力与重力的相对大小。

Fr数用于度量部分浸没的物体在流体中的阻力，较高的Fr值表示较高的流体阻力。

10 Weber数

韦伯数^[8]（We）表征惯性力与表面张力的相对大小。

式中，为表面张力系数。

参考资料