本文描述CFD理论中常用的矩阵、张量及其运算法则。

注：本文内容译自《The finite volume method in computational fluid dynamics _ an advanced introduction with OpenFOAM® and Matlab》，F.Moukalled, L.Mangani, M.Darwish

1 矩阵

一个阶的矩阵是一个矩形数组，其由行列数据组成。矩阵中第行第列的元素记作，如下面的矩阵元素的值为12。

因此，向量是一个的矩阵，标量是一个的矩阵。

阶的矩阵的转置矩阵是一个阶的矩阵，数学上可以表述为：

如果两个阶次相同的矩阵对应的元素都相等，那么这两个矩阵相等。两个相同阶次的矩阵可以逐元素加减。例如，矩阵、定义为：

则有及有：

矩阵与标量的乘积得到的矩阵为原矩阵的所有元素与标量的乘积：

两个矩阵的乘积较为复杂，其对矩阵的阶次存在要求。若矩阵与矩阵相乘，则要求矩阵的列数与矩阵的行数相等。如矩阵的阶次为，则矩阵的阶次必须为，它们的乘积矩阵的阶次为。矩阵的元素值为：

如矩阵为的矩阵，矩阵为的矩阵：

则矩阵是一个的矩阵：

2 方阵

若矩阵的行数与列数相等，则称矩阵为阶方阵。一个方阵的所有元素构成其主对角线（从左上角到右下角），方阵元素（其中）称之为矩阵的交叉对角线（从矩阵的左下角到右上角）。

方阵具有一些其它类型矩阵所不具有的特性，如对称性和反对称性。此外，许多运算（如取行列式和计算特征值等）只对方阵有意义。一个N阶方阵与自身相乘的结果仍然是一个N阶方阵，因此一个方阵可以根据需要与自身进行多次乘积运算，标记为矩阵与自身进行次乘积运算：

当方阵中的元素时（此时）称之为对称矩阵，当元素时称之为反对称矩阵。如下面的3阶方阵是一个对称方阵：

下面的4阶矩阵是一个反对称矩阵。

对角方阵D是一个除主对角外其它所有元素都是零的矩阵。下面的矩阵是一个3阶的对角方阵：

主对角线上的所有元素都是1的N阶对角矩阵称为N阶单位矩阵，通常标记为，如下为一个4阶单位矩阵：

方阵的逆矩阵的阶次与原矩阵相同，且有：

上三角矩阵是一个主对角线以下元素均为零的方阵，数学定义为：

下三角矩阵是一个主对角线以上所有元素均为零的方阵，其数学定义为：

如下面两个矩阵分别为上三角矩阵与下三角矩阵：

3 利用矩阵描述方程组

利用矩阵可以非常方便地描述方程组。一个有N个未知数N个方程的方程组可以写成：

可以将其转化为矩阵方程的形式：

写成紧凑形式的矩阵方程为：

4 矩阵的行列式

行列式是一个与方阵相关的值，其可以通过矩阵的元素通过一系列的数学方法及性能计算。方阵的行列式记作或，注意这里不是绝对值计算。

2阶矩阵的行列式的计算很简单，它是主对角线上元素的乘积减去交叉对角线上元素的乘积，可以表述为数学计算方式为：

对于高阶矩阵，这个过程更加复杂，并且基于余子式与代数余子式的概念。

元素的余子式为行列式中去除第行及第列后剩余的矩阵元素，其代数余子式为余子式的值与或的乘积，写成数学表达式为：

一个方阵 (N阶)的行列式是通过找到它的某行或列元素的代数余子式，将每个代数余子式与相应的元素相乘，然后将结果相加来进行计算的，数学表达为：

很容易得到一个N阶的上三角矩阵、下三角矩阵或对角矩阵的行列式是其主对角上的元素的乘积。

5 特征向量与特征值

当方阵与向量的乘积的方向与向量的方向相同时，可称向量为矩阵的一个特征向量。矩阵与其特征向量的乘积不会改变其方向，仅改变其大小。因此存在标量使得，此处的标量称之为矩阵的特征值。显然对于任意常数，向量是矩阵的特征向量，因为存在，因此一个缩放的特征向量依然是原矩阵的特征向量。

若矩阵是一个N阶对称矩阵，则显然其拥有一组线性无关的特征向量，而且可以证明特征向量集合不是唯一的。然而其对应的特征值（记作是唯一的，其值可以相当也可以不相等。单位矩阵的特征值均为1，且所有非零向量均为单位矩阵的特征向量。

通常，一个N阶方阵的特征值可以通过下面的方式求解得到：

根据定义，特征向量非零，则有：

可将方程展开为：

求解此方程即可得到特征值。

6 正定矩阵

N阶对称矩阵，若对任意列向量均满足以下不等式：

则称矩阵为正定矩阵。

如矩阵为3阶对称矩阵：

对于任意3阶向量，存在：

因此，矩阵是正定矩阵。

如果矩阵为N阶正定矩阵：

其具备以下一些特性：

• 矩阵的任意M阶()子矩阵也为正定矩阵。

• 矩阵的N个特征值均为正数
• 若矩阵的所有特征值均为正数，则矩阵为正定矩阵
• 若矩阵为正定矩阵，则矩阵可分解为，其中为下三角矩阵。

7 矩阵运算

若及为标量，为单位矩阵，为矩阵，存在以下的一些运算规则：

8 张量与张量运算

张量可以被看作是已经在定义标量和向量等量时所使用的思想的扩展。标量是一个秩为0的张量，而向量是一个秩为1的张量。高秩张量的主要用途是处理和变换方程组。在CFD中只需要秩为2的张量。与速度向量相似，CFD中常使用偏应力张量，如下图所示。这里以其作为张量介绍的对象。

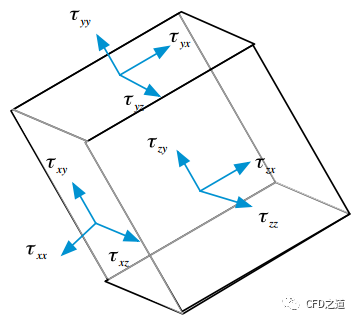
以表示正交笛卡尔坐标系中的三个方向，则应力张量及其转置形式以其分量值表示为：

张量也可以使用以表示的形式：

上式允许定义第三种向量积，其用于将两个向量相乘，称为向量并积（dyadic product），其结果为一个张量，它的分量由两个向量的有序对组成。具体地说，向量与其自身的向量并积为：

向量的梯度计算结果是一个张量：

两个张量和的和是一个张量，其分量是两个张量相应分量之和：

张量与标量的乘积仍然是一个张量，其分量为原张量的分量与标量的乘积：

张量与向量的点积结果是一个向量，表示为：

展开后可得到：

可进一步化简为：

上面的方程可以写成矩阵乘法的形式：

张量的散度是一个向量，计算结果为：