本文描述CFD理论中涉及较多的向量及其运算法则。

注：本文内容译自《The finite volume method in computational fluid dynamics _ an advanced introduction with OpenFOAM® and Matlab》，F.Moukalled, L.Mangani, M.Darwish

向量（Vector）有时也称为矢量。流体动力学中最常见的向量是速度向量，用表示。速度向量的分量在三维笛卡尔坐标系中沿x,y,z方向分别标记为u,v,w，如下图所示。

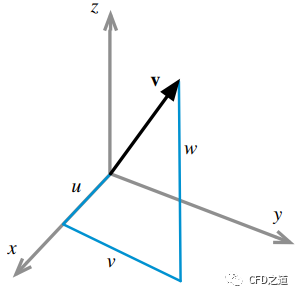
在笛卡尔坐标系中，向量可记为：

式中，分别为x,y,z方向的单位向量。向量通常表示为其转置的列向量形式：

向量的大小为：

向量与的和等于各向量分量的和，如：

或：

向量与标量相乘得到向量：

1 向量的点积

根据定义，两个向量和的点积是一个标量：

式中，为向量与向量的夹角的余弦值。根据向量点积的定义，有以下关系式：

以正交笛卡尔分量表示，两个向量与的点积可计算为：

2 向量的模

根据向量点积的计算规则，向量的模定义为：

3 单位方向向量

方向的单位向量可由向量的点积得到：

因此，一个向量在另一个向量方向上的分量可以看作是被投影的向量与另一个向量的单位方向的点积，如下图所示。

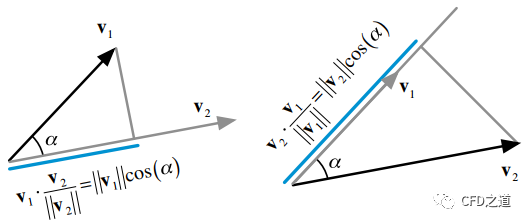
4 向量的叉乘

两个向量与的叉乘是一个向量。向量的方向为向量与构成的平面的法向，向量的模：

如下图所示。

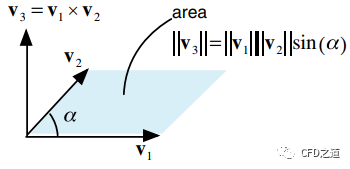
两个向量的叉乘的模为由这两个向量围成的平行四边形的面积。

很明显，两个共线向量的叉乘为零，因为它们围成的面积为零。两个正交单位向量的叉乘结果为一个垂直于两个单位向量的单位向量，向量的方向由右手定则来确定。叉乘运算如下：

根据上面的运算法则，两个向量的叉乘写成笛卡尔分量的形式可表示为：

上面的运算法则也可以写成行列式的形式：

5 标量三重积

三个向量可能存在以下的计算形式：，该形式可以利用行列式的方式进行计算：

标量三重积的绝对值表示由向量围成的平行六面体的体积。

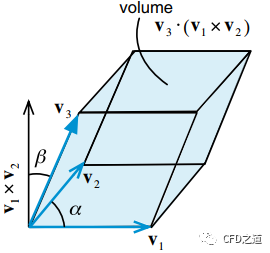
注：在CFD控制方程中，标量三重积经常会出现。

6 标量的梯度与方向导数

流体力学中经常出现的一个重要的向量运算符为，也称之为del或nabla算子，其定义为：

当运算符作用在标量上时得到该标量的梯度：

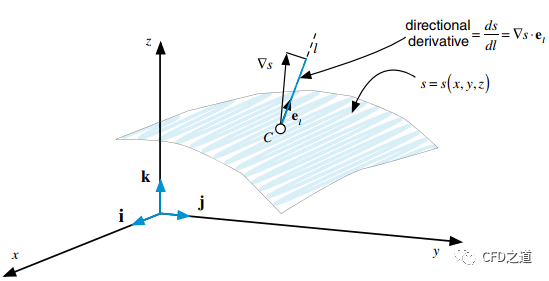
因此，标量场的梯度是一个向量场，表明标量s的值在大小和方向上随位置的变化而变化。

在单位向量上的投影可由下式获取：

该式称为标量沿单位向量方向的方向导数，如下图所示。方向导数的最大值为，且当时得到最大值，该方向为标量的梯度方向。

7 算子

对向量运用del算子，其结果为向量的散度，其值为一个标量，计算结果为：

该值也称之为向量场的散度，其结果为标量。

一个标量的梯度的散度依然为一个标量，其值可以用拉普拉斯算子表示：

对一个向量应用拉普拉斯算子，其计算结果依然为一个向量，计算结果为：

当算子与向量叉乘时得到的是向量场的旋度：

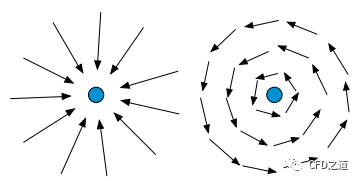
向量场的散度与旋度示意图如下图所示。左图所示的径向向量场只有散度，其旋度为零，在流体力学中，这个向量场表示存在汇或源的速度场。右图描述了一个只有旋度且散度为零的旋转向量场。这样的速度场相当于涡流的速度场。

在CFD控制方程中，常会出现向量场的散度与梯度，如：

8 其它的向量运算

若为标量，为向量场，下面是它们之间的一些运算法则：

注意：文中有些公式较长，注意向左滑动公式查看完整内容。