小白:残差是迭代法的副产品!
小白对CFD计算中的残差不太理解,而且对于大多数CFD软件利用残差用于判断计算是否收敛也是一知半解。
大清早来到实验室,小白发现空荡荡的房间里只有江师姐一个人,再看看墙上的钟,时间为7:15。“真是个勤奋的好孩纸啊”,小白心里嘀咕。
“这么早啊”,小白打招呼。
“早什么啊,还没下班呢。“江师姐头都懒得抬。
“啊,熬通宵了呀?这么拼命干啥子。”小白起身倒了一杯开水冲了一杯早餐牛奶。
“过两天项目要中期汇报,俺们的资料都没整理呢。”江师姐说。“到时候老蓝不让毕业,那才是真真的要人命呢。”
“对了,最近在忙些什么?上次给你的CFD秘笈目录看得怎样了?”江师姐停下手中的活计说道。
“天天上课啊,感觉没啥长进。对了江师姐,你说CFD计算为啥要用残差作为收敛判断的标准?”小白问。
“CFD计算用迭代法求解代数方程组,大家都知道迭代法是用循环的方式进行计算,那么问题来了,计算机程序中的循环必须要有中断条件,否则就成了死循环了。残差经常被用来作为迭代循环的中断条件。“江师姐说。
“那残差是如何作为中断条件的呢?”小白问。
“残差的概念来自于迭代法,指的是同一物理量在两次迭代之间的变化量。从理论上讲,因为方程组的解析解是唯一的,所以残差值应该为零。由于迭代法的初始解并非解析解,因此每一次迭代后的解都会存在差异,当然如果迭代格式很好的话,这个差异会逐渐降低且趋于零。大多数情况下迭代格式没有那么的完美,残差可能会下降到一定程度后不再下降了,此时为了结束循环迭代,可以设置当残差小于某一值后终止迭代。“江师姐解释道。
“我说的很粗糙,不过下面这个示例你可以仔细体会一下。”江师姐接着说。
1 迭代程序中的残差
如下列线性方程组。
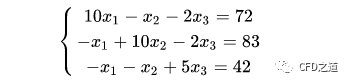
采用松弛迭代法求解,并输出三个未知量x1,x2及x3的残差变化曲线。
可以利用下面的程序代码来实现:
# -*- coding: utf-8 -*-#
import matplotlib.pyplot as plt
import numpy as np
def f(x1, x2, x3, count, w):
it = np.arange(1,count,1)
count =[]
x1r = []
x2r = []
x3r = []
for item in it:
y1 = x1-w*(x1-0.1*x2-0.2*x3-7.2)
y2 = x2-w*(-0.1*y1+x2-0.2*x3-8.3)
y3 = x3-w*(-0.2*y1 -0.2 *y2+x3-8.4)
if (max(abs(y1-x1), abs(y2-x2), abs(y3-x3)) < 0.00001):
# 设定残差为0.00001
print('求解结果:x1=%.5f、x2=%.5f、x3=%.5f'% (y1, y2, y3))
break;
else:
x1r.append(abs(y1 - x1))
x2r.append(abs(y2 - x2))
x3r.append(abs(y3 - x3))
count.append(item)
x1,x2,x3 = y1,y2,y3
plt.plot(count,x1r,'r',label='x1')
plt.plot(count,x2r,'b',label='x2')
plt.plot(count,x3r,'g',label='x3')
plt.grid()
plt.yscale('log')
plt.xlabel('Iteration')
plt.ylabel('Residual(log)')
plt.legend()
plt.show()
f(15,15,8,1000,0.5)江师姐:上面程序中的0.00001即为残差标准,该程序采用的是绝对残差,即同一变量的两次迭代结果的差的绝对值。实际应用中常采用相对残差,即用两次迭代差值再除以上一次的值。
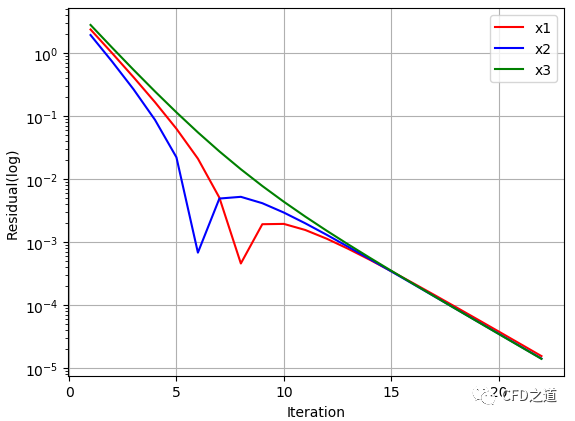
上面的代码采用松弛因子0.5进行计算,程序输出为:
求解结果:x1=10.99998、x2=11.99998、x3=12.99998
经过22次迭代达到收敛,输出的残差变化曲线如下图所示。
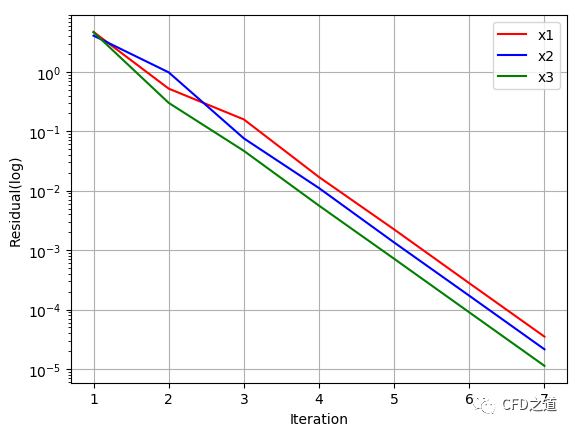
下图是改用松弛因子1.0计算的残差曲线。计算在迭代6步后达到收敛。
程序输出:
求解结果:x1=11.00000、x2=12.00000、x3=13.00000
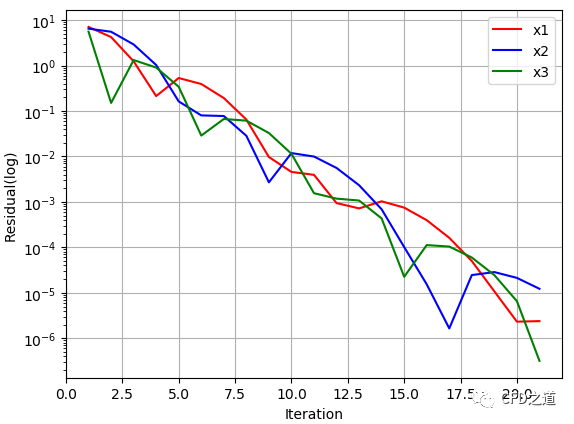
下图利用松弛因子1.5进行计算得到的残差图。计算在迭代21次后达到收敛。
虽然残差振荡得厉害,但代码输出结果依然得到了正确的解。
求解结果:x1=11.00000、x2=12.00000、x3=13.00000
需要注意的是:
-
上面采用的三种不同的松弛因子(0.5,1.0,1.5)进行计算,最终均收敛值1e-5,虽然残差曲线不同,但最终获取的计算结果是相同的,均为(11,12,13)。
-
残差降低到收敛标准,只能表示计算收敛,但无法证明结果正确与否。但是能确定的是,计算没有达到收敛,其结果肯定是不正确的。
-
残差标准在一定程度上可以控制计算精度
2 Fluent中的残差
以Fluent为例,CFD软件中也提供了残差设置方式。如下图所示。
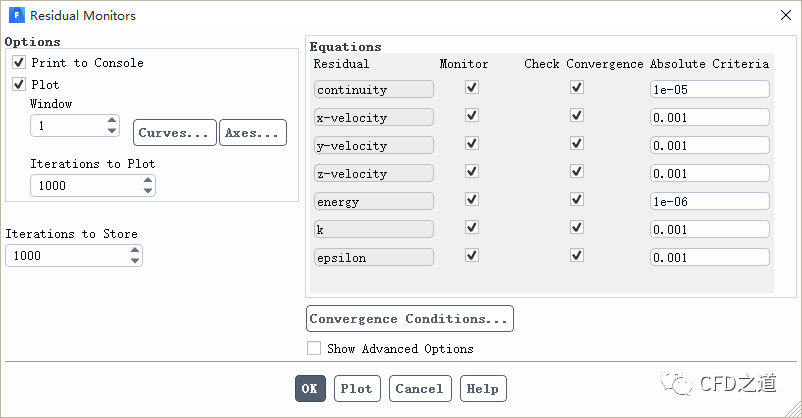
根据求解物理量的不同,所需要设置的残差标准数量也不同。默认情况下Fluent设置流动变量的残差标准为0.001,能量方程的残差标准为1E-6。大多数工程问题都是适合的。不过对于一些研究性的问题,通常要将残差标准降低,如降低到1e-5,二维问题建议将所有物理量的残差降低到1e-6。
江师姐:残差不是判断收敛的唯一标准!
小白系列往期列表:
本篇文章来源于微信公众号: CFD之道








评论前必须登录!
注册