小白:良好的开端意味着成功了一半!
受计算机内存限制,一些非线性方程以及大规模线性方程组的求解常采用迭代法进行求解。
1 迭代法
利用迭代法求解需要指定初始值,这初始值指定得好与坏,直接决定了计算收敛过程,不恰当的初始值甚至可能会导致计算发散。迭代法有很多种,常见的如牛顿法、赛德尔迭代等。
如求解一元三次方程:
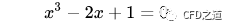
可令:
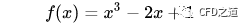
采用牛顿法列出迭代式为:
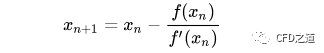
要利用上面的迭代式,必须指定初始值x0,否则迭代没办法进行下去。
可采用程序计算求解:
def f(x):return x**3-2 *x + 1# 计算导数def f_first_order(x):return 3*x**2 -2# x0为初始值,max_iter为迭代次数,tol为残差def get_root(x0, max_iter = 50, tol = 1e-7):p0 = x0 * 1.0print('初始值:p0=',p0)for i in range(max_iter):p = p0 - f(p0)/f_first_order(p0)if(abs(p - p0) < tol):return u'经过%s次迭代,估计的参数值为%.4f'%(i,p)p0 = pprint('第%s次迭代:p%s=%.6f'%(i+1,i+1,p0))print(u'已达到最大迭代次数,计算无法收敛')if __name__ == '__main__':print(get_root(2.0))
这里以x=2.0作为初始值进行求解,程序输出:
初始值:p0= 2.0
第1次迭代:p1=1.500000
第2次迭代:p2=1.210526
第3次迭代:p3=1.063280
第4次迭代:p4=1.008996
第5次迭代:p5=1.000232
第6次迭代:p6=1.000000
第7次迭代:p7=1.000000
经过87次迭代,估计的参数值为1.0000
可看出经过7次迭代,计算收敛,得到结果为1.0。
再尝试增大或减小初始值,如以10.0作为初始值,计算输出为:
初始值:p0= 10.0
第1次迭代:p1=6.708054
第2次迭代:p2=4.531768
第3次迭代:p3=3.105767
第4次迭代:p4=2.187116
第5次迭代:p5=1.613226
第6次迭代:p6=1.273671
第7次迭代:p7=1.092678
第8次迭代:p8=1.017296
第9次迭代:p9=1.000822
第10次迭代:p10=1.000002
第11次迭代:p11=1.000000
经过11次迭代,估计的参数值为1.0000
可以看出经过了11次迭代,得到计算结果1.0。
若以初始值1.2为初始值,计算输出为:
初始值:p0= 1.2
第1次迭代:p1=1.058621
第2次迭代:p2=1.007865
第3次迭代:p3=1.000178
第4次迭代:p4=1.000000
经过4次迭代,估计的参数值为1.0000
只需要4次迭代即可获得满足要求的结果。
多测试几组,如表所示。
| 初始值p0 | 迭代次数 | 收敛结果 |
|---|---|---|
| 1.2 | 5 | 1.0 |
| 2 | 8 | 1.0 |
| 10 | 12 | 1.0 |
| 100 | 18 | 1.0 |
| 500 | 21 | 1.0 |
| 5000 | 27 | 1.0 |
| 50000 | 33 | 1.0 |
该模型过于简单,也可以用复杂的代数方程组来进行试验。可以看出,初始值偏离结果值越远,所需的迭代次数越多。
2 迭代法求解方程组
上面的方程求根只有一个变量,自然非常简单。对于CFD计算中动辄几百万上千万个线性方程组的求解,指定一个好的初始值就没那么简单了。下面拿一个简单的方程组求解来看看。
利用迭代法如下所示的线性方程组:
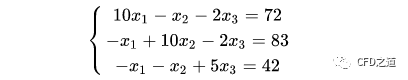
有人会说这个简单,小学生都能解。当然这里只有三个未知数,那如果位置说有三百万个呢,你还能用纸来解么?受内存限制,当方程数量过多,也没有办法采用直接法求解,内存一次读不下那么多数据啊。这里采用迭代法求解。迭代法求解线性方程组最简单的莫过于jacobi迭代。
先将上面的方程组改写成下面的形式:
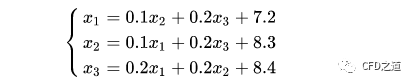
在利用jacobi迭代法改写成迭代式:
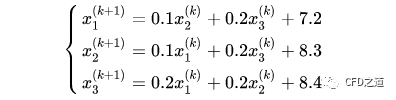
可以采用程序求解:
def f(x1,x2,x3,count=1):y1=0.1*x2+0.2*x3+7.2y2=0.1*x1+0.2*x3+8.3y3=0.2*x1+0.2*x2+8.4if abs(y1-x1)<0.0001 and abs(y2-x2)<0.0001 and abs(y3-x3)<0.0001:#设定精度为0.0001print('最终结果:%.4f、%.4f和%.4f'%(y1,y2,y3))else:print('第%s次迭代:%.4f、%.4f和%.4f'%(count, y1,y2,y3))x1,x2,x3,count=y1,y2,y3,count+1return f(x1,x2,x3,count)f(3,5,5)#设置初始根为(3,5,5)
这里设置初始值(3,5,5),计算输出为:
第1次迭代:8.7000、9.6000和10.0000
第2次迭代:10.1600、11.1700和12.0600
第3次迭代:10.7290、11.7280和12.6660
第4次迭代:10.9060、11.9061和12.8914
第5次迭代:10.9689、11.9689和12.9624
第6次迭代:10.9894、11.9894和12.9876
第7次迭代:10.9964、11.9964和12.9957
第8次迭代:10.9988、11.9988和12.9986
第9次迭代:10.9996、11.9996和12.9995
第10次迭代:10.9999、11.9999和12.9998
第11次迭代:11.0000、12.0000和12.9999
最终结果:11.0000、12.0000和13.0000
可以看出一共迭代了11次,计算收敛,得到解为(11,12,13)。
尝试采用比较接近最终解的初始值,如调用f(10,11,12),可得到输出:
第1次迭代:10.7000、11.7000和12.6000
第2次迭代:10.8900、11.8900和12.8800
第3次迭代:10.9650、11.9650和12.9560
第4次迭代:10.9877、11.9877和12.9860
第5次迭代:10.9960、11.9960和12.9951
第6次迭代:10.9986、11.9986和12.9984
第7次迭代:10.9995、11.9995和12.9994
第8次迭代:10.9998、11.9998和12.9998
第9次迭代:10.9999、11.9999和12.9999
最终结果:11.0000、12.0000和13.0000
迭代9次得到最终解。有兴趣的小伙伴也可以尝试其他偏离最终解的初始值代入计算,看看收敛性如何。
随着变量的增加,更难找到合适的初始值。
还有一个问题,这里有3个未知数,因此初始值需要提供3个值,那如果其中某一个值严重偏离目标值,计算结果会怎样呢?采用初始值(10,110,120),输出为:
第1次迭代:42.2000、33.3000和32.4000
第2次迭代:17.0100、19.0000和23.5000
第3次迭代:13.8000、14.7010和15.6020
第4次迭代:11.7905、12.8004和14.1002
第5次迭代:11.3001、12.2991和13.3182
第6次迭代:11.0935、12.0936和13.1198
第7次迭代:11.0333、12.0333和13.0374
第8次迭代:11.0108、12.0108和13.0133
第9次迭代:11.0037、12.0037和13.0043
第10次迭代:11.0012、12.0012和13.0015
第11次迭代:11.0004、12.0004和13.0005
第12次迭代:11.0001、12.0001和13.0002
第13次迭代:11.0000、12.0000和13.0001
最终结果:11.0000、12.0000和13.0000
可以看到,共迭代了13次才收敛到最终结果,随着初始值的偏离,计算迭代次数也会随之增多。
当然这里只有3个未知数,对于流体计算网格非常多的时候,未知数的数量也会随之增多,想要提供一个良好的初始值也就非常困难了。
3 Fluent中的初始化
由于CFD求解器多采用迭代法进行代数方程组的求解,因此在进行CFD计算之前,往往也需要对计算区域内的物理量的初始分布进行指定。
如Fluent提供了两种针对整体计算区域的初始化工具:
-
Hybrid Initialization:根据已有的边界条件采用求解Laplace方程的方式对全体计算区域赋予初始值。
-
Standard Initialization:采用显式指定物理量值的方式对全体计算区域赋予初始值。采用此种方式进行初始化后,物理量在整个计算区域内的分布为均匀分布。
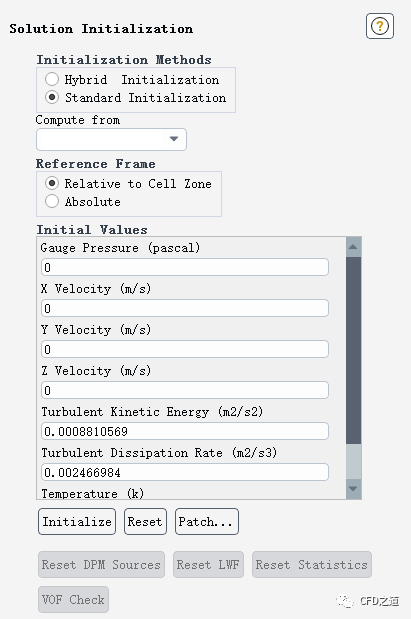
小白系列往期列表:
本篇文章来源于微信公众号: CFD之道








评论前必须登录!
注册