小白:一张一弛,文武之道也。
小白在了解到线性方程组的迭代法求解后,课上老师又降到了松弛迭代。小白听得是云里雾里。不过小白听从牛师兄的建议,自己动手编制程序,一番折腾下来也算是小有心得。
1 松弛迭代法求解方程组
考虑线性方程组:
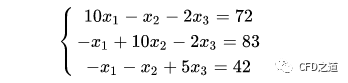
采用Gauss-Seidel迭代法将前面的方程组改写成迭代式:
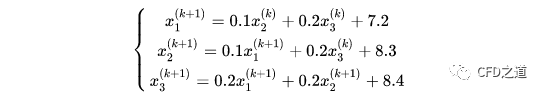
程序代码可写成:
#seidel 迭代法求根def f(x1,x2,x3,count=1):y1=0.1*x2+0.2*x3+7.2y2=0.1*y1+0.2*x3+8.3y3=0.2*y1+0.2*y2+8.4if max(abs(y1-x1), abs(y2-x2), abs(y3-x3))<0.0001:#设定精度为0.0001print('最终结果:%.4f、%.4f和%.4f' %(y1,y2,y3))else:print('第%s次迭代:%.4f、%.4f和%.4f' %(count, y1,y2,y3))x1,x2,x3,count=y1,y2,y3,count+1return f(x1,x2,x3,count)f(3,5,5)输出结果为:
第1次迭代:8.7000、10.1700和12.1740
第2次迭代:10.6518、11.8000和12.8904
第3次迭代:10.9581、11.9739和12.9864
第4次迭代:10.9947、11.9967和12.9983
第5次迭代:10.9993、11.9996和12.9998
第6次迭代:10.9999、11.9999和13.0000
最终结果:11.0000、12.0000和13.0000
可看出结果6次迭代计算收敛,得到解为(11,12,13)。
松弛迭代可以看成是高斯-赛德尔迭代的改进。一种简单的松弛迭代形式为:
小白:从松弛迭代形式可以看出,当计算收敛时,计算结果是不依赖于松弛因子w的取值的,因为当计算收敛时,括号中的值为零。
对应的程序代码:
复制复制复制#sor迭代法# -*- coding: utf-8 -*-#def f(x1, x2, x3, w=1, count=1):y1 = x1-w*(x1-0.1*x2-0.2*x3-7.2)y2 = x2-w*(-0.1*y1+x2-0.2*x3-8.3)y3 = x3-w*(-0.2*y1 -0.2 *y2+x3-8.4)if max(abs(y1-x1), abs(y2-x2), abs(y3-x3)) < 0.0001:# 设定精度为0.0001print('最终计算结果:%.4f、%.4f和%.4f' % (y1, y2, y3))else:print('第%s次迭代:%.4f、%.4f和%.4f' % (count, y1, y2, y3))x1, x2, x3, count = y1, y2, y3, count+1return f(x1, x2, x3, w, count)f(3,5,5,1) #设置松弛因子为1运行后输出:
第1次迭代:8.7000、10.1700和12.1740
第2次迭代:10.6518、11.8000和12.8904
第3次迭代:10.9581、11.9739和12.9864
第4次迭代:10.9947、11.9967和12.9983
第5次迭代:10.9993、11.9996和12.9998
第6次迭代:10.9999、11.9999和13.0000
最终计算结果:11.0000、12.0000和13.0000
可看到输出结果与赛德尔迭代完全相同。
注:松弛迭代法中,当松弛因子w=1时,即为高斯-赛德尔迭代;w>1时为超松弛迭代;w<1时为亚松弛迭代。
下面改变松弛因子看看有什么不同,验证结果如下表所示。
| 松弛因子 |
达到收敛时迭代次数 |
| 0.001 |
不收敛 |
| 0.01 |
952 |
| 0.1 |
124 |
| 0.5 |
23 |
| 0.75 |
13 |
| 1.0 |
6 |
| 1.25 |
9 |
| 1.5 | 18 |
| 1.75 |
41 |
| 2.0 |
不收敛 |
可以看到,不同的松弛因子会影响收敛的次数。
小白:在这个方程组中,松弛因子为1时收敛性表现最好。但要注意并非所有情况下都是松弛因子为1时收敛性最好。关于松弛因子与收敛性间的关系,可参阅任何一本数值分析教材。松弛因子并非越小越好,也并非越大越好,在实际计算过程中,需要根据收敛性来调整松弛因子的值。在一些方程组求解过程中,可能会出现迭代算法不稳定的情况,此时可以利用松弛因子控制方程的稳定性。
2 Fluent中的松弛因子
Fluent中采用的是亚松弛迭代。所有松弛因子取值范围为0~1。
鼠标双击模型树节点Solution > Controls,即可在右侧面板中设置松弛因子。
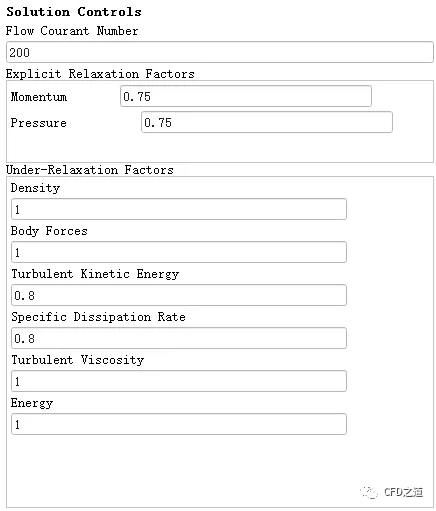
关于Fluent中的亚松弛因子:
取值范围0~1
取值越大,收敛越快,计算稳定性越差;取值越小,收敛越慢,稳定性更好
当残差震荡厉害时,可适当减小松弛因子;当残差曲线变化量很小且非常平缓时,可增大松弛因子
只要计算收敛,松弛因子不会影响计算结果
小白系列往期列表:
本篇文章来源于微信公众号: CFD之道

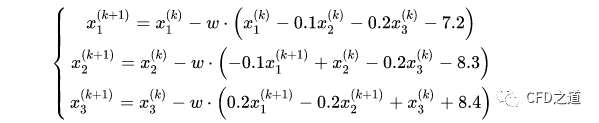







评论前必须登录!
注册