捣鼓了半天的迭代法求解线性方程组,小白却越来越迷糊了。“线性方程组哪里来的?数学物理方程中的物理模型不都是偏微分方程吗?跟线性方程组有啥关系?“小白很是不解。
“师兄,这么巧啊,啥时候回来的?”小白问。牛师兄最近被老蓝派到大漠采集实验数据,都两个月没见到人了。
“嗯,不是一般的好玩哟,下次让老蓝派你去。嘿嘿。“牛师兄开玩笑道。
“天天上课,无聊得一比啊。对了师兄,我们最近在学数值分析,里面有提到代数方程组的各种求解方法,为什么代数方程组的求解如此重要呢?我看到数学物理方程那门课中提到现实世界中的物理问题通常使用微分方程进行描述的啊。“小白说。
“嗯,物理现象常常用微分方程进行描述,比如流体流动问题我们常用NS方程进行描述,这NS方程就是微分方程。至于说为何数值分析中花那么大的篇幅去讲线性方程组的求解,是因为在微分方程的数值求解中,常常是将转化为线性方程组利用计算机进行求解。“牛师兄说。
“采用解析方法求解微分方程难度很大,这个你学过数学物理方程的课,应该有所感受。将微分方程转化为代数方程,利用计算机求解转化后的代数方程,则相对要容易不少。”牛师兄补充道。
“为何是方程组?这就要扯到从微分方程到代数方程的转换过程了。我们都知道微分方程是连续的,而计算机处理连续问题则非常麻烦,将连续的微分方程转化为不连续的代数方程组之后,利用计算机求解则容易多了。这里将连续的微分方程转为不连续的代数方程组的过程,我们常称之为离散。”牛师兄说。
“离散的方法有很多,比如你们上课学习的有限单元法就是其中一种,除此之外,比较常用的离散方法还有有限差分法、有限体积法等。流体计算早期常用有限差分法,现在普遍采用有限体积法。“牛师兄接着说。
“其实也不麻烦,你去图书馆找本计算流体力学的书,里面都会讲到的。”牛师兄说。
1 一个简单的离散例子
考虑如下的一维稳态无源热传导方程,其控制方程可表达为:
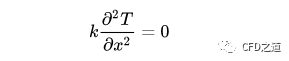
上述偏微分方程结构很简单,容易求得其解析解。将其利用有限差分法采用中心差分离散可得到:
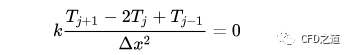
式中下标j+1、j以及j-1均为为节点编号,Δx为网格间距,基于下图所示的网格系统。

简单实例:如图所示的一维稳态圆棒内的无源导热问题,横截面均匀的圆棒长度为1m,其两端分别保持温度为100℃和500℃。求解圆棒内的温度分布。已知导热系数k=1000W/(m.K),横截面积A=0.001m2。
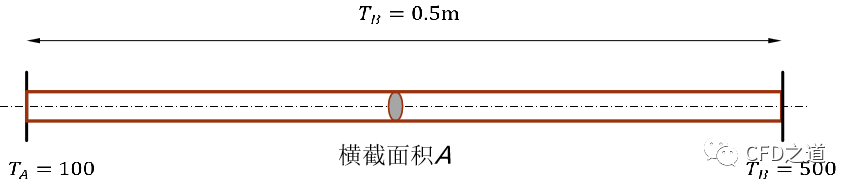

采用等间距网格,其间距Δx=0.2 m。此时可代入离散方程得到:
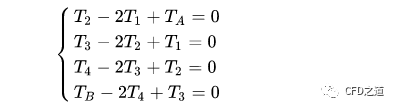
将TA=100,TB=500代入到方程组,即可得到矩阵方程:
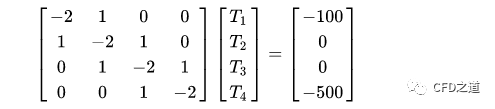

相同方式,可以采用更加细密的计算网格进行计算,同时矩阵方程的阶数也会增加。(这里采用4个内部节点,矩阵方程为4阶)
2 简单讨论
“通过这个简单的例子,看明白其中的规律了么?”牛师兄问小白。
“嗯,大致有点儿感觉了,离散是连续微分方程转化为数量有限的的代数方程组,在转化的过程中,离散格式很重要,网格系统也很重要。”小白说。
“是的,其实这两个也是离散算法的基础。不同的离散算法,其采用的网格系统不太一样,所使用的离散格式也不同。”牛师兄说。
“上面简单的案例是用有限差分法进行离散的,实际上也可以用有限体积法或有限元法进行离散,同样也可以得到线性方程组。”牛师兄补充道。
“得到方程组后,就可以用各种迭代算法来进行求解了。从方程组可以看出,网格数量越多,离散后的代数方程组数量也越多,待求的变量也越多,方程组阶数越大,计算量也越大。“牛师兄接着说。
本篇文章来源于微信公众号: CFD之道
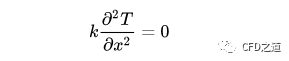
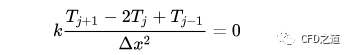



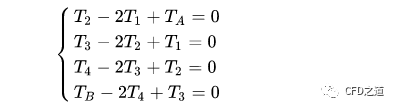
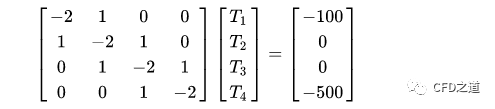

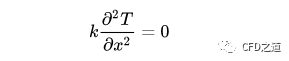
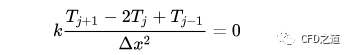



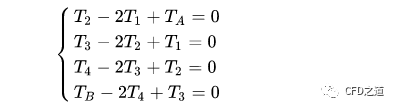
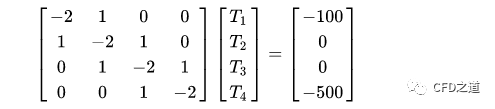



评论前必须登录!
注册