小白：迭代法实际上是用时间换空间！

小白最近在学习《数值分析》，其中有讲到代数方程组的求解方式，然而课堂上老师讲得很快，小白听得稀里糊涂的，一堂课下来就记住了几个以前在线性代数中学过的什么高斯消去法，克拉默法，还有什么迭代法。

1 直接法求解

以下列线性方程组举例采用直接法求解。

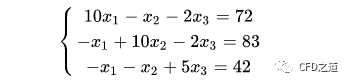
最简单的直接法求解莫过于矩阵求逆。如上面的代数方程可表达为以下的矩阵方程：

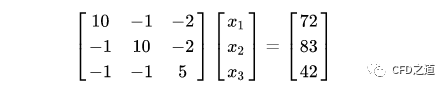
可求解得到：

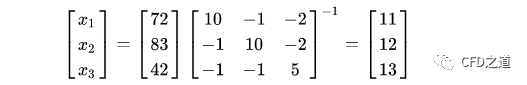
在利用直接法求解过程中，不管系数矩阵有多复杂，在计算过程中均需要一次性读入内存。直接法有很多种，比如常见的高斯消去法、克拉默法等。

上述方程组也可以采用高斯消去法进行求解。基本方法为：

小白：在进行CFD计算过程中，代数方程的系数矩阵可能有几百万几千万阶（跟网格数量有关系），要将如此庞大的矩阵一次性读入计算机，会消耗矩量的内存。打个简单的比方，如计算100万个网格，对每个变量都存在一个100万x100万的矩阵方程，若不考虑矩阵的稀疏性，将100万x100万矩阵存入内存，保守估计需要1000G的内存。当然在实际程序设计中可以应用一些存储技巧来节省计算内存，但实际计算也有网格数量远超100万的情况，如果是1000万网格呢，可能需要100T的内存了。所以实际的CFD程序中，很少有采用直接法求解代数方程组，大多数采用迭代法进行求解。

2 迭代法求解方程组

考虑线性方程组：

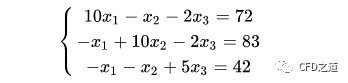
采用迭代法进行求解。

1.1 Jacobi迭代

迭代法求解线性方程组最简单的莫过于jacobi迭代。

在利用jacobi迭代法改写成迭代式：

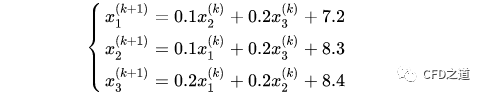
可以采用程序求解：

def f(x1,x2,x3,count=1):      y1=0.1*x2+0.2*x3+7.2      y2=0.1*x1+0.2*x3+8.3      y3=0.2*x1+0.2*x2+8.4      if abs(y1-x1)<0.0001 and abs(y2-x2)<0.0001 and abs(y3-x3)<0.0001:            #设定精度为0.0001            print('最终的计算结果为%s、%s和%s' %(y1,y2,y3))      else:            print('第%s次迭代的计算结果为%s、%s和%s' %(count, y1,y2,y3))            x1,x2,x3,count=y1,y2,y3,count+1            return f(x1,x2,x3,count)f(3,5,5)#设置初始值为(3,5,5)

小白：迭代法并不需要将方程组所有系数一次性全部读入内存。求解过程中是采用顺序求解，一次只计算一个代数方程，100万个方程组成的方程组，一次完整迭代需要计算100万次，但每一次只需要读入少量的数据。这里的一次完整迭代对应于流体计算中的一个迭代步。所以当网格数量很多时，计算一步也需要很长的时间。

这里设置初始值（3,5,5），计算输出为：

第1次迭代的计算结果为8.7、9.60和10.0

第2次迭代的计算结果为10.16、11.1700和12.06

第3次迭代的计算结果为10.7290、11.728和12.666

第4次迭代的计算结果为10.9063、11.9061和12.8914

第5次迭代的计算结果为10.9688、11.9688和12.9624

第6次迭代的计算结果为10.9893、11.989373和12.9875

第7次迭代的计算结果为10.9964、11.9964和12.9957

第8次迭代的计算结果为10.9987946、11.9987和12.9985

第9次迭代的计算结果为10.999、11.99和12.9

第10次迭代的计算结果为10.9998、11.9998和12.9998

第11次迭代的计算结果为10.9999、11.9999和12.9999

最终的计算结果为10.9999、11.999和12.9999

可以看出一共迭代了11次，计算收敛，得到解为（11,12,13）。

1.2 Gauss-seidel迭代

在Jacobi迭代中，后面的迭代并没有应用到前面的结果。Gauss-Seidel迭代与之不同，后面的迭代利用到了前面的计算结果，如下所示，将前面的方程组改写成迭代式：

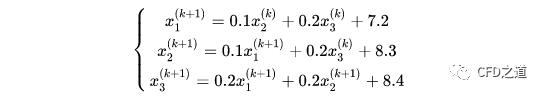
程序代码可写成：

#seidel 迭代法求根def f(x1,x2,x3,count=1):      y1=0.1*x2+0.2*x3+7.2      y2=0.1*y1+0.2*x3+8.3      y3=0.2*y1+0.2*y2+8.4      if max(abs(y1-x1), abs(y2-x2), abs(y3-x3))<0.0001:            #设定精度为0.0001            print('最终的计算结果为%s、%s和%s' %(y1,y2,y3))      else:            print('第%s次迭代的计算结果为%s、%s和%s' %(count, y1,y2,y3))            x1,x2,x3,count=y1,y2,y3,count+1            return f(x1,x2,x3,count) f(3,5,5)#设置初始根为(3,5,5)

输出结果为：

第1次迭代的计算结果为8.7、10.17和12.174

第2次迭代的计算结果为10.6518、11.7999和12.89

第3次迭代的计算结果为10.9583、11.9738和12.9863

第4次迭代的计算结果为10.9946、11.9967和12.9982

第5次迭代的计算结果为10.999、11.9995和12.9997

第6次迭代的计算结果为10.9999、11.9999和12.9999

最终的计算结果为10.9999、11.9999和12.9999

可看出结果6次迭代计算收敛，得到解为（11,12,13）。