小白最近逛图书馆,发现最近关于Fluent的书是越来越多了,而且还发现这些关于Fluent教材中的案例都大同小异。小白接受小牛师兄的建议,找了一本结构比较鲜明的书照着上面的案例就练了起来。不过当练习的案例多了,小白却发现了一个问题“在建立计算模型时,为什么有时候采用二维模型,而有时候又采用三维模型?二维模型和三维模型的差异在哪里?二维代替三维到底有没有问题?”带着这些问题,小白找到了小牛师兄。
“师兄,你说Fluent中计算的二维模型到底有没有意义呢?”小白问。
“怎么会没有意义呢,当然有意义啊,当你计算机性能不行的时候,你就会知道能算二维是一件多么有意义的事情了。”小牛师兄说。
“可是,现实世界中不可能存在二维的物体啊。”小白说。
“嗯,这倒是真的,现实世界的任何物体都是三维的,不存在没有厚度的面,也不存在没有截面积的线,更不存在没有体积的点,所有的这一切都是近似的。但是近似并不表示一定就不行,实际上在很多时候利用这些近似,可以获得不错的结果。”小牛师兄说。
“那什么时候可以利用这种简化呢?比如说用二维代替三维模型。”小白问。
“我们常说的以二维模型来近似模拟三维模型,只是针对某一维尺寸远小于另外两维的情况下。这时候需要注意的是,采用二维模型时无法考虑法向方向的物理信息,在进行二维几何模型计算过程中,常常将面法向方向简化为常数,即总是认为面几何体的厚度为定值(通常默认为1 m)。在CFD中,二维模型一般都为平面模型。”小牛师兄说。
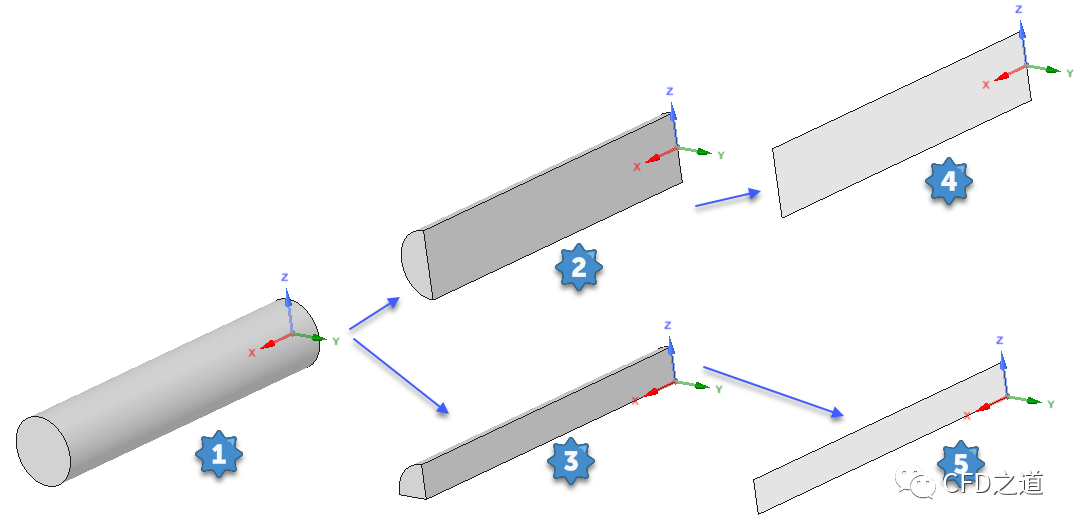
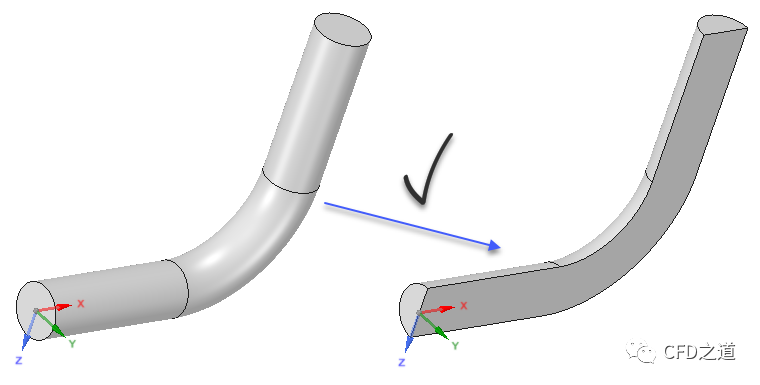
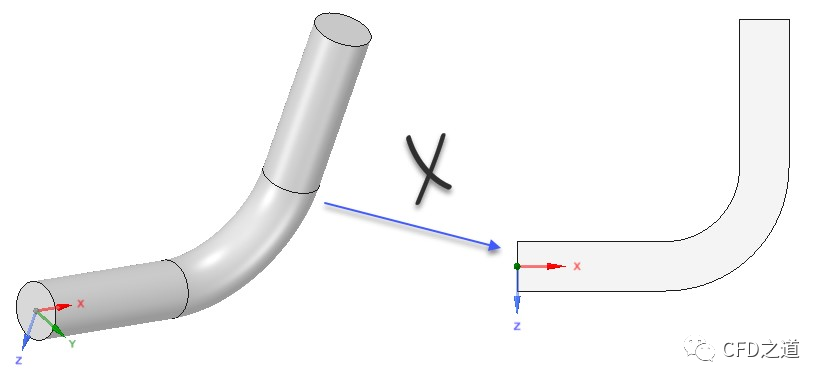
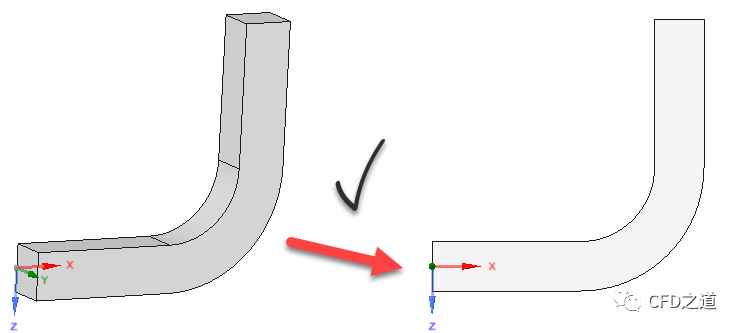
“我在做案例的时候,碰到过很奇怪的问题。比如说计算一个管道内部流动,有的案例采用三维几何模型,如图1所示;有的案例用半个三维几何,如图2所示;有的案例采用四分之一模型,如图3所示;有的案例采用管道纵剖面几何(二维矩形),如图四所示;而有的案例又采用二维的半剖面几何(矩形),如图5所示。这个到底该怎么选呢?”小白问。
“通常来说,采用全三维模型自然是不存在任何问题的,对于比较简单的几何模型强烈建议使用全三维模型,因为其能提供所有的信息。在流场对称的情况下可利用对称性采用半模型或四分之一模型,当然严格意义上的流场对称是不存在的,不过有时候这种简化是可以认可的。比如图2所示的模型,如果沿对称面法向方向没有外部力作用则可以使用,但如果有外部力(如重力等)沿法向方向,则不可使用。图3也是一样,对称面法向法向不允许有外部力存在。至于图4和图5的简化,则除了要求外部力方向不能沿面法向之外,还必须假设流场特性在任意方向截面分布一致。”小牛师兄说。
1 案例测试
计算模型为图1所示的直管道,截面直径10mm,长度100mm。入口面流速 0.1 m/s,出口采用静压 0 Pa。流体介质为水。雷诺数约为1000,采用层流计算。
2 计算结果
以下采用相同计算条件得到的速度云图分布(从左至右分别对应上图1-5模型)。
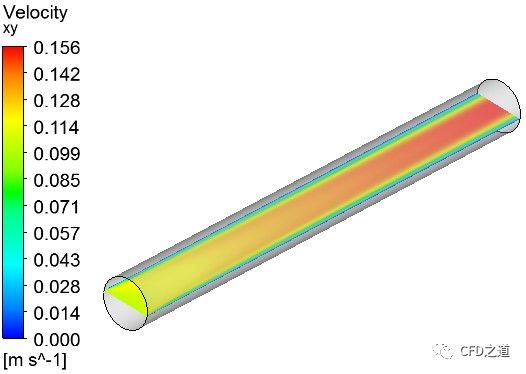
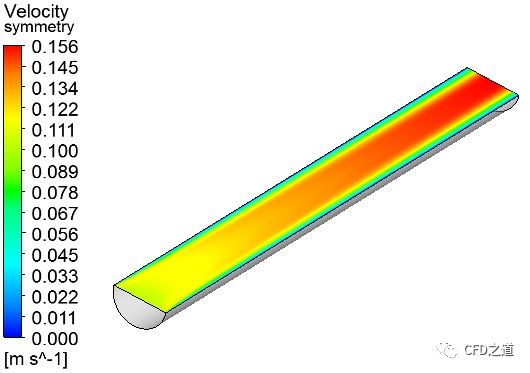
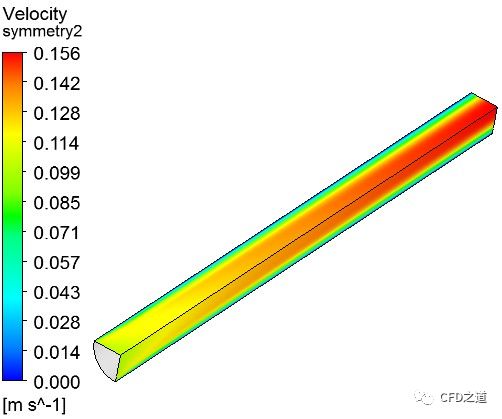
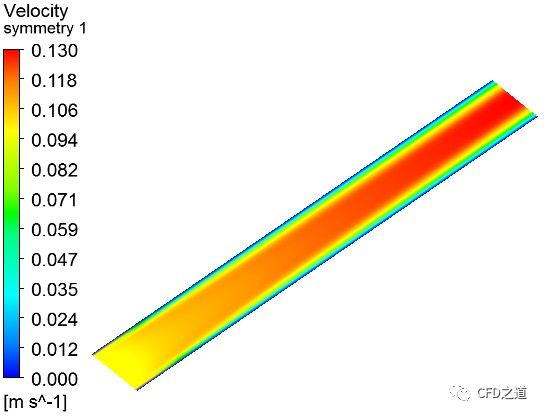
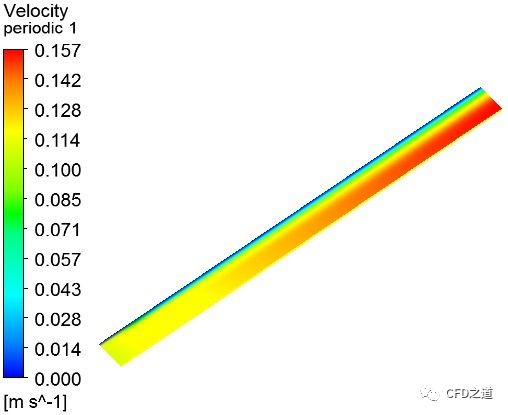
分析:从图中看出,五种不同模型计算得到的速度分布趋势基本保持一致,但是利用模型4计算得到的最大速度明显小于其他四种模型计算得到的结果。
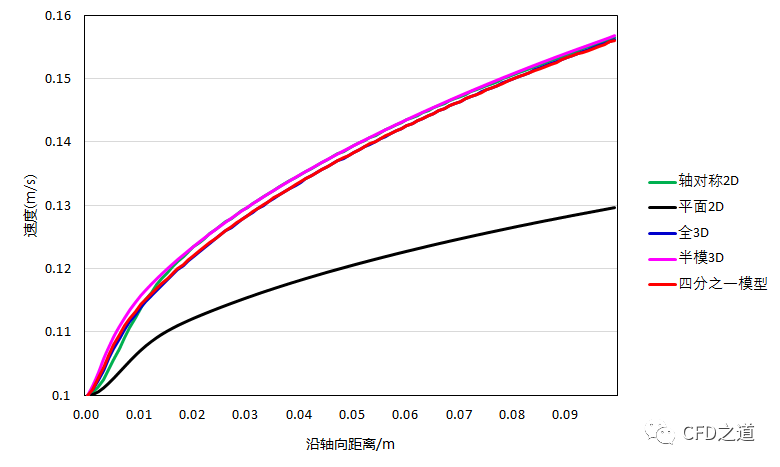
根据理论计算结果,充分发展的核心最大速度应为平均速度的2倍,即 0.2 m/s。
3 改进计算
将计算区域延长,从当前的0.1m延长至0.4m重新计算。从上图可以看出,采用轴对称方式计算结果能够与3D模型相吻合,因此改进计算只采用两种平面模型。
下图为延长至0.4m后的两种模型计算结果,可以看到最大速度已经非常接近理论值 0.2m/s。而2D平面模型计算的最大值小于0.15m/s,距离理论值相去甚远。
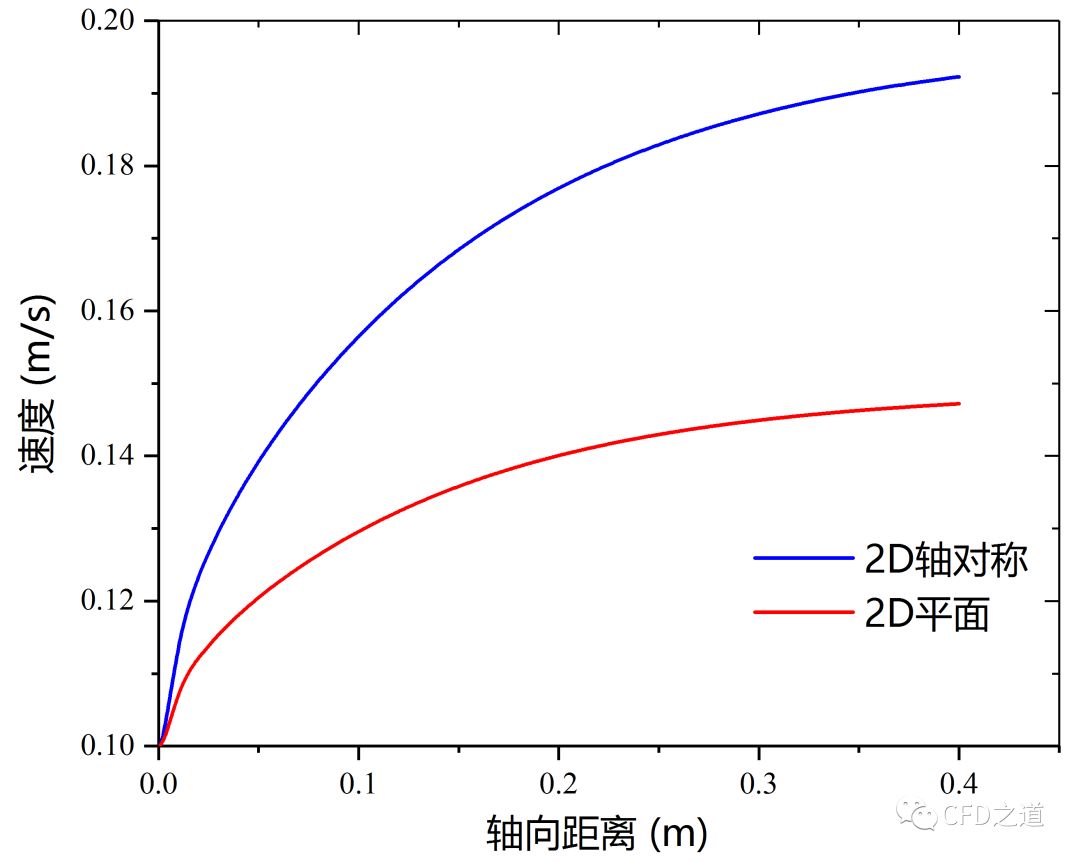
总结:对于类似直管流动问题,采用全3D模型,半3D模型、四分之一3D模型以及轴对称二维模型都可接受,但是2D平面模型是不可接受的。
原因分析:2D平面模型实际上是当做拉伸体而不是旋转体计算,拉伸厚度默认为1m。在计算过程中对于平面法向方向的考虑与真实的圆柱体不相符。
4 其他问题
实际上很多的模型都存在这样的限制,在使用2D平面模型时需要格外注意,其只适用于厚度相对于其他两个维度非常小的拉伸体的简化,对于回转体则不适用。
本篇文章来源于微信公众号: CFD之道



















评论前必须登录!
注册