本文利用Julia计算二维管道内压力驱动流动。

管道内压力驱动流动的控制方程如下：

与方腔流动唯一的区别在于U动量方程中多了一个源项F，以模拟压力驱动的影响。

1 离散形式

u-动量方程的离散形式为：

离散v动量方程：

离散压力泊松方程：

改写为迭代式的形式。

2 初始值与边界值

初始条件下，计算区域内。

对于边界条件：

y=0及y=2为对称边界，；

x=0及x=2边界，为周期边界

所有区域，

3 代码

using PyPlot
matplotlib.use("TkAgg")
 
function buildUpB(rho, dt, dx, dy, u, v)
    b = zeros(size(u))
    b[2:end-1, 2:end-1] =
        rho * (
            1 / dt * (
                (u[2:end-1, 3:end] - u[2:end-1, 1:end-2]) / (2 * dx) +
                (v[3:end, 2:end-1] - v[1:end-2, 2:end-1]) / (2 * dy)
            ) - ((u[2:end-1, 3:end] - u[2:end-1, 1:end-2]) / (2 * dx)) .^ 2 -
            2 * (
                (u[3:end, 2:end-1] - u[1:end-2, 2:end-1]) / (2 * dy) .*
                (v[2:end-1, 3:end] - v[2:end-1, 1:end-2]) / (2 * dx)
            ) - ((v[3:end, 2:end-1] - v[1:end-2, 2:end-1]) / (2 * dy)) .^ 2
        )
 
    ####Periodic BC Pressure @ x = 2
    b[2:end-1, end] =
        rho * (
            1 / dt * (
                (u[2:end-1, 1] - u[2:end-1, end-1]) / (2 * dx) +
                (v[3:end, end] - v[1:end-2, end]) / (2 * dy)
            ) - ((u[2:end-1, 1] - u[2:end-1, end-1]) / (2 * dx)) .^ 2 -
            2 * (
                (u[3:end, end] - u[1:end-2, end]) / (2 * dy) .*
                (v[2:end-1, 1] - v[2:end-1, end-1]) / (2 * dx)
            ) - ((v[3:end, end] - v[1:end-2, end]) / (2 * dy)) .^ 2
        )
 
    ####Periodic BC Pressure @ x = 0
    b[2:end-1, 1] =
        rho * (
            1 / dt * (
                (u[2:end-1, 2] - u[2:end-1, end]) / (2 * dx) +
                (v[3:end, 1] - v[1:end-2, 1]) / (2 * dy)
            ) - ((u[2:end-1, 2] - u[2:end-1, end]) / (2 * dx)) .^ 2 -
            2 * (
                (u[3:end, 1] - u[1:end-2, 1]) / (2 * dy) .*
                (v[2:end-1, 2] - v[2:end-1, end]) / (2 * dx)
            ) - ((v[3:end, 1] - v[1:end-2, 1]) / (2 * dy)) .^ 2
        )
 
    return b
end
 
function presPoissPeriodic(p, dx, dy)
    pn = zeros(size(p))
 
    for q = 1:nit
        pn = copy(p)
        p[2:end-1, 2:end-1] =
            (
                (pn[2:end-1, 3:end] + pn[2:end-1, 1:end-2]) * dy^2 +
                (pn[3:end, 2:end-1] + pn[1:end-2, 2:end-1]) * dx^2
            ) / (2 * (dx^2 + dy^2)) -
            dx^2 * dy^2 / (2 * (dx^2 + dy^2)) * b[2:end-1, 2:end-1]
 
        ####Periodic BC Pressure @ x = 2
        p[2:end-1, end] =
            (
                (pn[2:end-1, 1] + pn[2:end-1, end-1]) * dy^2 +
                (pn[3:end, end] + pn[1:end-2, end]) * dx^2
            ) / (2 * (dx^2 + dy^2)) -
            dx^2 * dy^2 / (2 * (dx^2 + dy^2)) * b[2:end-1, end]
 
        ####Periodic BC Pressure @ x = 0
        p[2:end-1, 1] =
            (
                (pn[2:end-1, 2] + pn[2:end-1, end]) * dy^2 +
                (pn[2:end-1, 1] + pn[1:end-2, 1]) * dx^2
            ) / (2 * (dx^2 + dy^2)) -
            dx^2 * dy^2 / (2 * (dx^2 + dy^2)) * b[2:end-1, 1]
 
        ####Wall boundary conditions, pressure
        p[end, :] = p[end-1, :]     ##dp/dy = 0 at y = 2
        p[1, :] = p[2, :]      ##dp/dy = 0 at y = 0
    end
    return p
end
 
##variable declarations
nx = 41;
ny = 41;
nt = 10;
nit = 50;
c = 1;
dx = 2 / (nx - 1);
dy = 2 / (ny - 1);
x = range(0, 2, length = nx);
y = range(0, 2, length = ny);
xgrid = repeat(x', nx, 1);
ygrid = repeat(y, 1, ny);
 
##physical variables
rho = 1;
nu = 0.1;
F = 1;
dt = 0.01;
 
#initial conditions
u = zeros((ny, nx)); ##create a XxY vector of 0's
v = zeros((ny, nx)); ##create a XxY vector of 0's
p = ones((ny, nx)); ##create a XxY vector of 0's
pn = ones((ny, nx)); ##create a XxY vector of 0's
 
b = zeros((ny, nx));
 
udiff = 1;
stepcount = 0;
 
while udiff > 0.001
    un = copy(u)
    vn = copy(v)
 
    b = buildUpB(rho, dt, dx, dy, u, v)
    p = presPoissPeriodic(p, dx, dy)
 
    u[2:end-1, 2:end-1] =
        un[2:end-1, 2:end-1] -
        un[2:end-1, 2:end-1] .* dt / dx .*
        (un[2:end-1, 2:end-1] - un[2:end-1, 1:end-2]) -
        vn[2:end-1, 2:end-1] .* dt / dy .*
        (un[2:end-1, 2:end-1] - un[1:end-2, 2:end-1]) -
        dt / (2 * rho * dx) * (p[2:end-1, 3:end] - p[2:end-1, 1:end-2]) +
        nu * (
            dt / dx^2 * (
                un[2:end-1, 3:end] - 2 * un[2:end-1, 2:end-1] +
                un[2:end-1, 1:end-2]
            ) +
            dt / dy^2 * (
                un[3:end, 2:end-1] - 2 * un[2:end-1, 2:end-1] +
                un[1:end-2, 2:end-1]
            )
        ) +
        F * dt
 
    v[2:end-1, 2:end-1] =
        vn[2:end-1, 2:end-1] -
        un[2:end-1, 2:end-1] .* dt / dx .*
        (vn[2:end-1, 2:end-1] - vn[2:end-1, 1:end-2]) -
        vn[2:end-1, 2:end-1] .* dt / dy .*
        (vn[2:end-1, 2:end-1] - vn[1:end-2, 2:end-1]) -
        dt / (2 * rho * dy) * (p[3:end, 2:end-1] - p[1:end-2, 2:end-1]) +
        nu * (
            dt / dx^2 * (
                vn[2:end-1, 3:end] - 2 * vn[2:end-1, 2:end-1] +
                vn[2:end-1, 1:end-2]
            ) + (
                dt / dy^2 * (
                    vn[3:end, 2:end-1] - 2 * vn[2:end-1, 2:end-1] +
                    vn[1:end-2, 2:end-1]
                )
            )
        )
 
    ####Periodic BC u @ x = 2    
    u[2:end-1, end] =
        un[2:end-1, end] -
        un[2:end-1, end] .* dt / dx .* (un[2:end-1, end] - un[2:end-1, end-1]) -
        vn[2:end-1, end] .* dt / dy .* (un[2:end-1, end] - un[1:end-2, end]) -
        dt / (2 * rho * dx) * (p[2:end-1, 1] - p[2:end-1, end-1]) +
        nu * (
            dt / dx^2 *
            (un[2:end-1, 1] - 2 * un[2:end-1, end] + un[2:end-1, end-1]) +
            dt / dy^2 *
            (un[3:end, end] - 2 * un[2:end-1, end] + un[1:end-2, end])
        ) +
        F * dt
 
    ####Periodic BC u @ x = 0
    u[2:end-1, 1] =
        un[2:end-1, 1] -
        un[2:end-1, 1] .* dt / dx .* (un[2:end-1, 1] - un[2:end-1, end]) -
        vn[2:end-1, 1] .* dt / dy .* (un[2:end-1, 1] - un[1:end-2, 1]) -
        dt / (2 * rho * dx) * (p[2:end-1, 2] - p[2:end-1, end]) +
        nu * (
            dt / dx^2 *
            (un[2:end-1, 2] - 2 * un[2:end-1, 1] + un[2:end-1, end]) +
            dt / dy^2 * (un[3:end, 1] - 2 * un[2:end-1, 1] + un[1:end-2, 1])
        ) +
        F * dt
 
    ####Periodic BC v @ x = 2
    v[2:end-1, end] =
        vn[2:end-1, end] -
        un[2:end-1, end] .* dt / dx .* (vn[2:end-1, end] - vn[2:end-1, end-1]) -
        vn[2:end-1, end] .* dt / dy .* (vn[2:end-1, end] - vn[1:end-2, end]) -
        dt / (2 * rho * dy) * (p[3:end, end] - p[1:end-2, end]) +
        nu * (
            dt / dx^2 *
            (vn[2:end-1, 1] - 2 * vn[2:end-1, end] + vn[2:end-1, end-1]) + (
                dt / dy^2 *
                (vn[3:end, end] - 2 * vn[2:end-1, end] + vn[1:end-2, end])
            )
        )
 
    ####Periodic BC v @ x = 0
    v[2:end-1, 1] =
        vn[2:end-1, 1] -
        un[2:end-1, 1] .* dt / dx .* (vn[2:end-1, 1] - vn[2:end-1, end]) -
        vn[2:end-1, 1] .* dt / dy .* (vn[2:end-1, 1] - vn[1:end-2, 1]) -
        dt / (2 * rho * dy) * (p[3:end, 1] - p[1:end-2, 1]) +
        nu * (
            dt / dx^2 *
            (vn[2:end-1, 2] - 2 * vn[2:end-1, 1] + vn[2:end-1, end]) +
            (dt / dy^2 * (vn[3:end, 1] - 2 * vn[2:end-1, 1] + vn[1:end-2, 1]))
        )
 
 
    ####Wall BC: u,v = 0 @ y = 0,2
    u[1, :] .= 0
    u[end, :] .= 0
    v[1, :] .= 0
    v[end, :] .= 0
 
    udiff = (sum(u) - sum(un)) / sum(u)
    stepcount += 1
end
 
fig = figure(figsize = (11, 7), dpi = 100)
quiver(
    xgrid[1:3:end, 1:3:end],
    ygrid[2:3:end, 2:3:end],
    u[2:3:end, 2:3:end],
    v[2:3:end, 2:3:end],
);
 
fig = figure(figsize = (11, 7), dpi = 100)
quiver(x, y, u, v);
PyPlot.show()

计算结果如图所示。

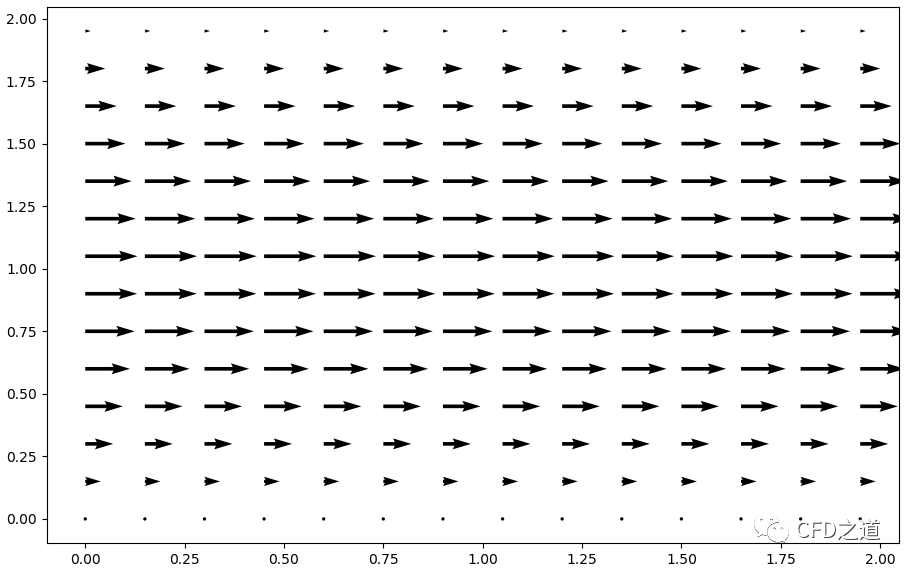
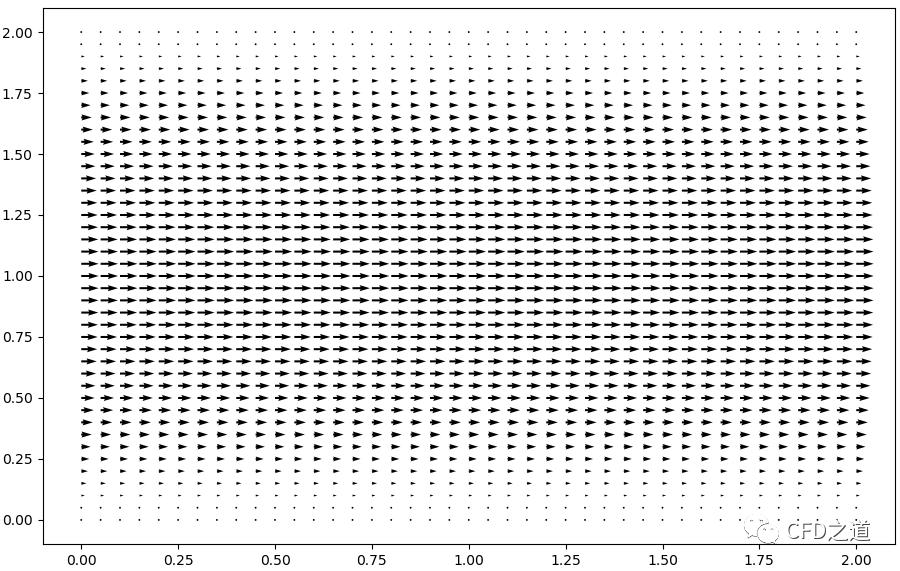
矢量图显示结果如下图所示。