本文利用Julia计算方腔顶盖流动。

密闭空腔中的流体流动满足下面的控制方程：

1 离散方程

离散U动量方程：

离散v动量方程：

离散压力泊松方程：

改写为迭代式的形式。

2 初始值与边界值

初始条件下，计算区域内。

对于边界条件：

y=2边界，；

y=0边界，；

y=2边界，；

x=0及x=2边界，

3 代码

using PyPlot
matplotlib.use("TkAgg")
nx = 41;
ny = 41;
nt = 500;
nit = 50;
c = 1;
dx = 2 / (nx - 1);
dy = 2 / (ny - 1);
x = range(0, 2, length = nx);
y = range(0, 2, length = ny);
 
rho = 1;
nu = 0.1;
dt = 0.001;
 
u = zeros((ny, nx));
v = zeros((ny, nx));
p = zeros((ny, nx));
b = zeros((ny, nx));

定义源项b。

function buildUpB(b, rho, dt, u, v, dx, dy)
    b[2:end-1, 2:end-1] =
        rho * (
            1 / dt * (
                (u[2:end-1, 3:end] - u[2:end-1, 1:end-2]) / (2 * dx) +
                (v[3:end, 2:end-1] - v[1:end-2, 2:end-1]) / (2 * dy)
            ) - ((u[2:end-1, 3:end] - u[2:end-1, 1:end-2]) / (2 * dx))^2 -
            2 * (
                (u[3:end, 2:end-1] - u[1:end-2, 2:end-1]) / (2 * dy) *
                (v[2:end-1, 3:end] - v[2:end-1, 1:end-2]) / (2 * dx)
            ) - ((v[3:end, 2:end-1] - v[1:end-2, 2:end-1]) / (2 * dy))^2
        )
    return b
end

定义压力泊松方程。

function presPoisson(p, dx, dy, b)
    pn = zeros(size(p))
    pn = copy(p)
 
    for q = 1:nit
        pn = copy(p)
        p[2:end-1, 2:end-1] =
            (
                (pn[2:end-1, 3:end] + pn[2:end-1, 1:end-2]) * dy^2 +
                (pn[3:end, 2:end-1] + pn[1:end-2, 2:end-1]) * dx^2
            ) / (2 * (dx^2 + dy^2)) -
            dx^2 * dy^2 / (2 * (dx^2 + dy^2)) * b[2:end-1, 2:end-1]
 
        p[:, end] = p[:, end-1] ##dp/dy = 0 at x = 2
        p[1, :] = p[2, :]  ##dp/dy = 0 at y = 0
        p[:, 1] = p[:, 2]    ##dp/dx = 0 at x = 0
        p[end, :] .= 0      ##p = 0 at y = 2
    end
    return p
end
 

计算方腔流动。

function cavityFlow(nt, u, v, dt, dx, dy, p, rho, nu)
    b = zeros((ny, nx))
 
    for n = 1:nt
        un = copy(u)
        vn = copy(v)
 
        b = buildUpB(b, rho, dt, u, v, dx, dy)
        p = presPoisson(p, dx, dy, b)
 
        u[2:end-1, 2:end-1] =
            un[2:end-1, 2:end-1] -
            un[2:end-1, 2:end-1] * dt / dx *
            (un[2:end-1, 2:end-1] - un[2:end-1, 1:end-2]) -
            vn[2:end-1, 2:end-1] * dt / dy *
            (un[2:end-1, 2:end-1] - un[1:end-2, 2:end-1]) -
            dt / (2 * rho * dx) * (p[2:end-1, 3:end] - p[2:end-1, 1:end-2]) +
            nu * (
                dt / dx^2 * (
                    un[2:end-1, 3:end] - 2 * un[2:end-1, 2:end-1] +
                    un[2:end-1, 1:end-2]
                ) +
                dt / dy^2 * (
                    un[3:end, 2:end-1] - 2 * un[2:end-1, 2:end-1] +
                    un[1:end-2, 2:end-1]
                )
            )
 
        v[2:end-1, 2:end-1] =
            vn[2:end-1, 2:end-1] -
            un[2:end-1, 2:end-1] * dt / dx *
            (vn[2:end-1, 2:end-1] - vn[2:end-1, 1:end-2]) -
            vn[2:end-1, 2:end-1] * dt / dy *
            (vn[2:end-1, 2:end-1] - vn[1:end-2, 2:end-1]) -
            dt / (2 * rho * dy) * (p[3:end, 2:end-1] - p[1:end-2, 2:end-1]) +
            nu * (
                dt / dx^2 * (
                    vn[2:end-1, 3:end] - 2 * vn[2:end-1, 2:end-1] +
                    vn[2:end-1, 1:end-2]
                ) + (
                    dt / dy^2 * (
                        vn[3:end, 2:end-1] - 2 * vn[2:end-1, 2:end-1] +
                        vn[1:end-2, 2:end-1]
                    )
                )
            )
 
        u[1, :] .= 0
        u[:, 1] .= 0
        u[:, end] .= 0
        u[end, :] .= 1    #set velocity on cavity lid equal to 1
        v[1, :] .= 0
        v[end, :] .= 0
        v[:, 1] .= 0
        v[:, end] .= 0
 
    end
    return u, v, p
end
 

计算100步，查看计算结果。

u = zeros((ny, nx));
v = zeros((ny, nx));
p = zeros((ny, nx));
b = zeros((ny, nx));
nt = 100;
u, v, p = cavityFlow(nt, u, v, dt, dx, dy, p, rho, nu);
 
fig = figure(figsize = (11, 7), dpi = 100)
contourf(x, y, p, alpha = 0.5)    ###plnttong the pressure field as a contour
colorbar()
contour(x, y, p)               ###plotting the pressure field outlines
xgrid = repeat(x', nx, 1)
ygrid = repeat(y, 1, ny)
quiver(
    xgrid[1:2:end, 1:2:end],
    ygrid[1:2:end, 1:2:end],
    u[1:2:end, 1:2:end],
    v[1:2:end, 1:2:end],
) ##plotting velocity
PyPlot.xlabel('X')
PyPlot.ylabel('Y');
PyPlot.show()

计算结果如下图所示。

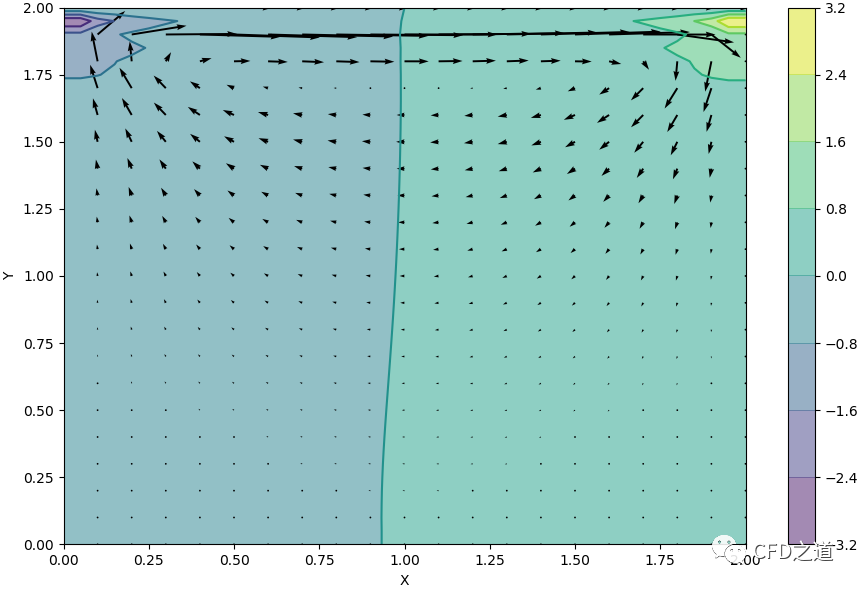
迭代计算700步查看计算结果。

u = zeros((ny, nx));
v = zeros((ny, nx));
p = zeros((ny, nx));
b = zeros((ny, nx));
nt = 700;
u, v, p = cavityFlow(nt, u, v, dt, dx, dy, p, rho, nu);
fig = figure(figsize = (11, 7), dpi = 100);
contourf(x, y, p, alpha = 0.5);
colorbar();
contour(x, y, p);
quiver(
    xgrid[1:2:end, 1:2:end],
    ygrid[1:2:end, 1:2:end],
    u[1:2:end, 1:2:end],
    v[1:2:end, 1:2:end],
); ##plotting velocity
xlabel('X');
ylabel('Y');
 

计算结果如下图所示。

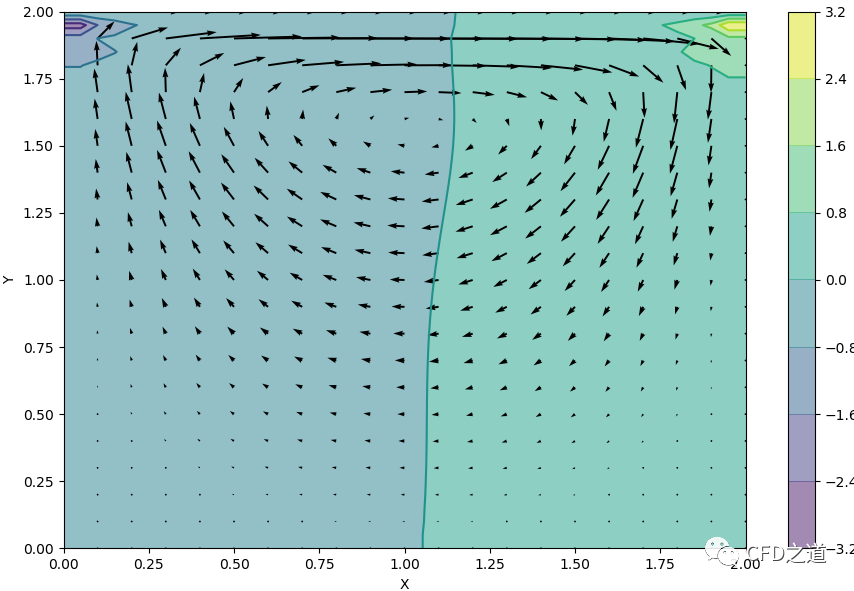
采用下面的代码查看流线。

fig = figure(figsize = (11, 7), dpi = 100);
contourf(x, y, p, alpha = 0.5,cmap = ColorMap("viridis"));
colorbar();
contour(x, y, p,cmap=ColorMap("viridis"));
xgrid = repeat(x', nx, 1)
ygrid = repeat(y, 1, ny)
streamplot(
    xgrid[1:2:end, 1:2:end],
    ygrid[1:2:end, 1:2:end],
    u[1:2:end, 1:2:end],
    v[1:2:end, 1:2:end],
)
PyPlot.xlabel("x")
PyPlot.ylabel("y")
PyPlot.show()

流线显示如下图所示。

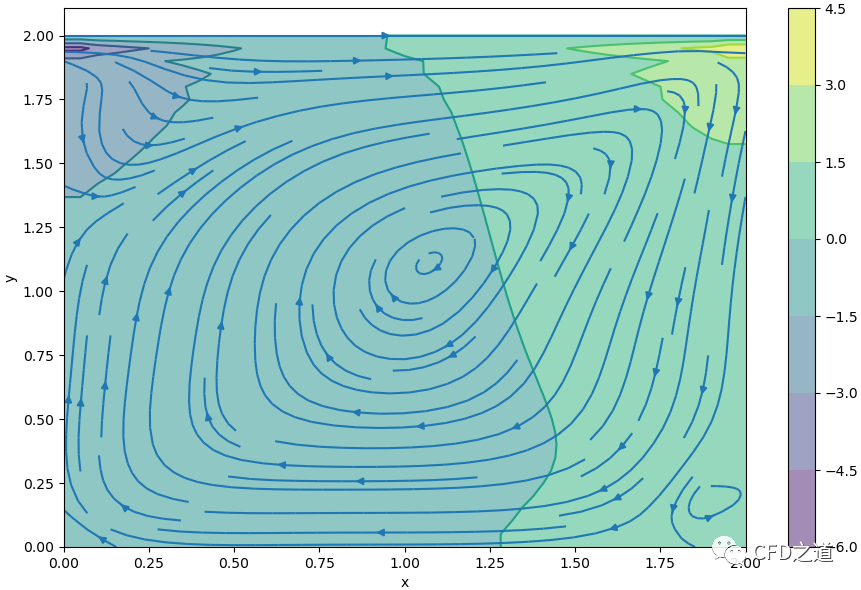
完整代码如下。

using PyPlot
matplotlib.use("TkAgg")
nx = 41;
ny = 41;
nt = 500;
nit = 50;
c = 1;
dx = 2 / (nx - 1);
dy = 2 / (ny - 1);
x = range(0, 2, length = nx);
y = range(0, 2, length = ny);
 
rho = 1;
nu = 0.1;
dt = 0.001;
 
u = zeros((ny, nx));
v = zeros((ny, nx));
p = zeros((ny, nx));
b = zeros((ny, nx));
 
 
function buildUpB(b, rho, dt, u, v, dx, dy)
    b[2:end-1, 2:end-1] =
        rho * (
            1 / dt * (
                (u[2:end-1, 3:end] - u[2:end-1, 1:end-2]) / (2 * dx) +
                (v[3:end, 2:end-1] - v[1:end-2, 2:end-1]) / (2 * dy)
            ) - ((u[2:end-1, 3:end] - u[2:end-1, 1:end-2]) / (2 * dx))^2 -
            2 * (
                (u[3:end, 2:end-1] - u[1:end-2, 2:end-1]) / (2 * dy) *
                (v[2:end-1, 3:end] - v[2:end-1, 1:end-2]) / (2 * dx)
            ) - ((v[3:end, 2:end-1] - v[1:end-2, 2:end-1]) / (2 * dy))^2
        )
    return b
end
 
function presPoisson(p, dx, dy, b)
    pn = zeros(size(p))
    pn = copy(p)
 
    for q = 1:nit
        pn = copy(p)
        p[2:end-1, 2:end-1] =
            (
                (pn[2:end-1, 3:end] + pn[2:end-1, 1:end-2]) * dy^2 +
                (pn[3:end, 2:end-1] + pn[1:end-2, 2:end-1]) * dx^2
            ) / (2 * (dx^2 + dy^2)) -
            dx^2 * dy^2 / (2 * (dx^2 + dy^2)) * b[2:end-1, 2:end-1]
 
        p[:, end] = p[:, end-1] ##dp/dy = 0 at x = 2
        p[1, :] = p[2, :]  ##dp/dy = 0 at y = 0
        p[:, 1] = p[:, 2]    ##dp/dx = 0 at x = 0
        p[end, :] .= 0      ##p = 0 at y = 2
    end
    return p
end
 
function cavityFlow(nt, u, v, dt, dx, dy, p, rho, nu)
    b = zeros((ny, nx))
 
    for n = 1:nt
        un = copy(u)
        vn = copy(v)
 
        b = buildUpB(b, rho, dt, u, v, dx, dy)
        p = presPoisson(p, dx, dy, b)
 
        u[2:end-1, 2:end-1] =
            un[2:end-1, 2:end-1] -
            un[2:end-1, 2:end-1] * dt / dx *
            (un[2:end-1, 2:end-1] - un[2:end-1, 1:end-2]) -
            vn[2:end-1, 2:end-1] * dt / dy *
            (un[2:end-1, 2:end-1] - un[1:end-2, 2:end-1]) -
            dt / (2 * rho * dx) * (p[2:end-1, 3:end] - p[2:end-1, 1:end-2]) +
            nu * (
                dt / dx^2 * (
                    un[2:end-1, 3:end] - 2 * un[2:end-1, 2:end-1] +
                    un[2:end-1, 1:end-2]
                ) +
                dt / dy^2 * (
                    un[3:end, 2:end-1] - 2 * un[2:end-1, 2:end-1] +
                    un[1:end-2, 2:end-1]
                )
            )
 
        v[2:end-1, 2:end-1] =
            vn[2:end-1, 2:end-1] -
            un[2:end-1, 2:end-1] * dt / dx *
            (vn[2:end-1, 2:end-1] - vn[2:end-1, 1:end-2]) -
            vn[2:end-1, 2:end-1] * dt / dy *
            (vn[2:end-1, 2:end-1] - vn[1:end-2, 2:end-1]) -
            dt / (2 * rho * dy) * (p[3:end, 2:end-1] - p[1:end-2, 2:end-1]) +
            nu * (
                dt / dx^2 * (
                    vn[2:end-1, 3:end] - 2 * vn[2:end-1, 2:end-1] +
                    vn[2:end-1, 1:end-2]
                ) + (
                    dt / dy^2 * (
                        vn[3:end, 2:end-1] - 2 * vn[2:end-1, 2:end-1] +
                        vn[1:end-2, 2:end-1]
                    )
                )
            )
 
        u[1, :] .= 0
        u[:, 1] .= 0
        u[:, end] .= 0
        u[end, :] .= 1    #set velocity on cavity lid equal to 1
        v[1, :] .= 0
        v[end, :] .= 0
        v[:, 1] .= 0
        v[:, end] .= 0
 
    end
    return u, v, p
end
 
#
# u = zeros((ny, nx));
# v = zeros((ny, nx));
# p = zeros((ny, nx));
# b = zeros((ny, nx));
# nt = 100;
# u, v, p = cavityFlow(nt, u, v, dt, dx, dy, p, rho, nu);
#
# fig = figure(figsize = (11, 7), dpi = 100)
# contourf(x, y, p, alpha = 0.5)    ###plnttong the pressure field as a contour
# colorbar()
# contour(x, y, p)               ###plotting the pressure field outlines
# xgrid = repeat(x', nx, 1)
# ygrid = repeat(y, 1, ny)
# quiver(
#     xgrid[1:2:end, 1:2:end],
#     ygrid[1:2:end, 1:2:end],
#     u[1:2:end, 1:2:end],
#     v[1:2:end, 1:2:end],
# ) ##plotting velocity
# PyPlot.xlabel('X')
# PyPlot.ylabel('Y');
# PyPlot.show()
 
u = zeros((ny, nx));
v = zeros((ny, nx));
p = zeros((ny, nx));
b = zeros((ny, nx));
nt = 700;
u, v, p = cavityFlow(nt, u, v, dt, dx, dy, p, rho, nu);
fig = figure(figsize = (11, 7), dpi = 100);
contourf(x, y, p, alpha = 0.5,cmap = ColorMap("viridis"));
colorbar();
contour(x, y, p,cmap=ColorMap("viridis"));
xgrid = repeat(x', nx, 1)
ygrid = repeat(y, 1, ny)
streamplot(
    xgrid[1:2:end, 1:2:end],
    ygrid[1:2:end, 1:2:end],
    u[1:2:end, 1:2:end],
    v[1:2:end, 1:2:end],
)
PyPlot.xlabel("x")
PyPlot.ylabel("y")
PyPlot.show()
 
# contourf(x, y, p, alpha = 0.5);
# colorbar();
# contour(x, y, p);
# quiver(
#     xgrid[1:2:end, 1:2:end],
#     ygrid[1:2:end, 1:2:end],
#     u[1:2:end, 1:2:end],
#     v[1:2:end, 1:2:end],
# ); ##plotting velocity
# xlabel('X');
# ylabel('Y');
 
PyPlot.show()