二维拉普拉斯方程为：

拉普拉斯方程通常采用中心差分进行离散。离散方程为：

整理为迭代形式：

注：

拉普拉斯方程是一个稳态模型。

”

计算区域内部初始条件，边界条件为：

对于此边界条件和初始条件，可以有解析解：

代码

using PyPlot
matplotlib.use("TkAgg")
 
function plot2D(x,y,p)
    fig = PyPlot.figure(figsize=(11,7),dpi=100)
    PyPlot.plot_surface(x,y,p,rstride=1,cstride=1,cmap=ColorMap("coolwarm"))
    xlim(0,2)
    ylim(0,1)
    xlabel("x(m)")
    ylabel("y(m)")
    zlabel("p(Pa)")
    PyPlot.show()
end

定义拉普拉斯模型计算函数。

 
# normal_target为收敛残差
function laplace2D(p,y,dx,dy,l1norm_target)
    l1norm = 1;
    pn = zeros(size(p))
    tol = 1000;
    count = 1;
    while (l1norm > l1norm_target || count < tol)
        pn = copy(p);
        p[2:end-1,2:end-1] = (dy^2*(pn[2:end-1,3:end]+pn[2:end-1,1:end-2])+dx^2*(pn[3:end,2:end-1]+pn[1:end-2,2:end-1]))/(2*(dx^2+dy^2))
 
        p[:,1] .= 0;       ##p = 0 @ x = 0
        p[:,end] = y;      ##p = y @ x = 2
        p[1,:] = p[2,:]  ##dp/dy = 0 @ y = 0
        p[end,:] = p[end-1,:]    ##dp/dy = 0 @ y = 1
        l1norm = LinearAlgebra.norm((p-pn)./pn,1)
        count +=1;
    end
    return p
end

定义一些变量参数。

 
##variable declarations
nx = 31;
ny = 31;
c = 1;
dx = 2/(nx-1);
dy = 2/(ny-1);
 
##初始条件
p = zeros((ny,nx)) ;
x = range(0,2,length = nx);
y = range(0,1,length = ny);
 
##边界条件
p[:,1] .= 0;
p[:,end] = y;
p[1,:] = p[2,:];
p[end,:] = p[end-1,:];
# plot2D(x, y, p)
 
p = laplace2D(p, y, dx, dy, 1e-4);
plot2D(x, y, p)

下面可以利用查看初始值分布。

plot2D(x,y,p)

初始分布如下图所示。

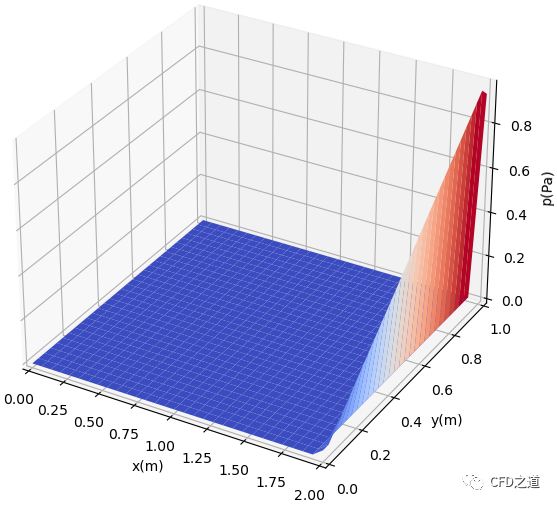
变量p在区域内取值为0，在x=2的位置，p的值等于y的值。

下面利用laplace2d函数计算并显示计算结果。

p = laplace2d(p,y,dx,dy,1e-4)
plot2D(x,y,p)

计算结果如下图所示。

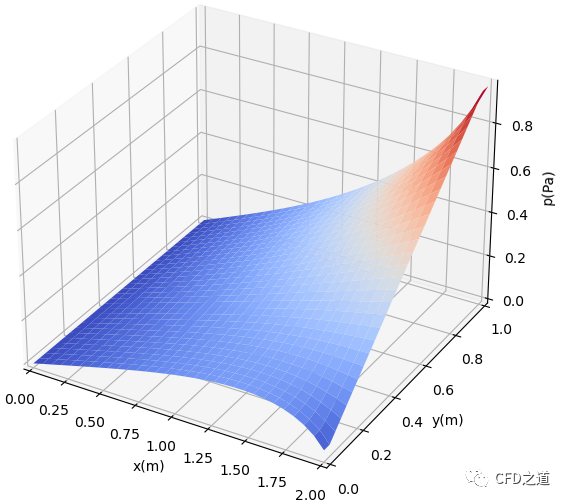
完整代码如下所示。

using PyPlot
using LinearAlgebra
matplotlib.use("TkAgg")
 
function plot2D(x,y,p)
    fig = PyPlot.figure(figsize=(11,7),dpi=100)
    PyPlot.plot_surface(x,y,p,rstride=1,cstride=1,cmap=ColorMap("coolwarm"))
    xlim(0,2)
    ylim(0,1)
    xlabel("x(m)")
    ylabel("y(m)")
    zlabel("p(Pa)")
    PyPlot.show()
end
 
# normal_target为收敛残差
function laplace2D(p,y,dx,dy,l1norm_target)
    l1norm = 1;
    pn = zeros(size(p))
    tol = 1000;
    count = 1;
    while (l1norm > l1norm_target || count < tol)
        pn = copy(p);
        p[2:end-1,2:end-1] = (dy^2*(pn[2:end-1,3:end]+pn[2:end-1,1:end-2])+dx^2*(pn[3:end,2:end-1]+pn[1:end-2,2:end-1]))/(2*(dx^2+dy^2))
 
        p[:,1] .= 0;       ##p = 0 @ x = 0
        p[:,end] = y;      ##p = y @ x = 2
        p[1,:] = p[2,:]  ##dp/dy = 0 @ y = 0
        p[end,:] = p[end-1,:]    ##dp/dy = 0 @ y = 1
        l1norm = LinearAlgebra.norm((p-pn)./pn,1)
        count +=1;
    end
    return p
end
 
##variable declarations
nx = 31;
ny = 31;
c = 1;
dx = 2/(nx-1);
dy = 2/(ny-1);
 
##初始条件
p = zeros((ny,nx)) ;
x = range(0,2,length = nx);
y = range(0,1,length = ny);
 
##边界条件
p[:,1] .= 0;
p[:,end] = y;
p[1,:] = p[2,:];
p[end,:] = p[end-1,:];
# plot2D(x, y, p)
 
p = laplace2D(p, y, dx, dy, 1e-4);
plot2D(x, y, p)