二维Burgers方程描述为：

对其进行离散，可表示为：

整理成迭代形式为：

Julia代码

using PyPlot
matplotlib.use("TkAgg")
 
nx = 41
ny = 41
nt = 120
c = 1
dx = 2 / (nx - 1)
dy = 2 / (ny - 1)
sigma = 0.0009
nu = 0.01
dt = sigma * dx * dy / nu;
 
x = range(0, 2, length = nx)
y = range(0, 2, length = ny)
 
u = ones((ny, nx))
v = ones((ny, nx))
comb = ones((ny, nx))
 
# 初始条件
u[floor(Int, 0.5 / dy):floor(Int, 1 / dy),floor(Int, 0.5 / dx):floor(Int, 1 / dx),] .= 2
v[floor(Int, 0.5 / dy):floor(Int, 1 / dy),floor(Int, 0.5 / dx):floor(Int, 1 / dx),] .= 2
 
PyPlot.plot_wireframe(x,y,u,cmap=ColorMap("coolwarm"))
PyPlot.show()

绘制初始条件分布如下图所示。

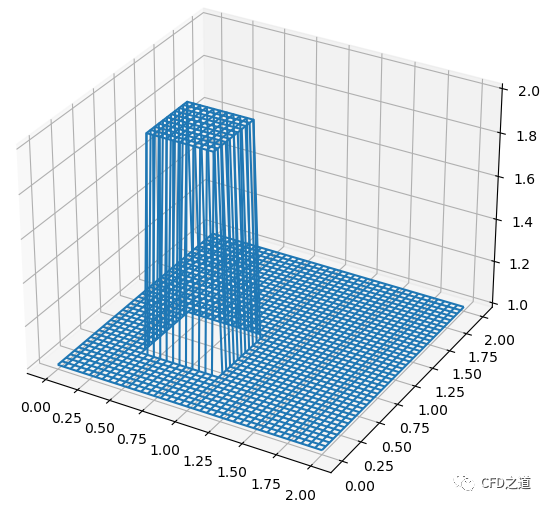
迭代计算代码如下所示。

for n in 1:nt
    un =copy(u)
    vn =copy(v)
    u[2:end-1,2:end-1] = un[2:end-1,2:end-1] - dt/dx*un[2:end-1,2:end-1].*(un[2:end-1,2:end-1]-un[2:end-1,1:end-2])-
dt/dy*vn[2:end-1,2:end-1].*(un[2:end-1,2:end-1]-un[1:end-2,2:end-1])+
nu*dt/dx^2*(un[2:end-1,3:end]-2*un[2:end-1,2:end-1]+un[2:end-1,1:end-2])+
nu*dt/dy^2*(un[3:end,2:end-1]-2*un[2:end-1,2:end-1]+un[3:end,2:end-1])
 
   v[2:end-1,2:end-1] = vn[2:end-1,2:end-1] - dt/dx*un[2:end-1,2:end-1].*(vn[2:end-1,2:end-1]-vn[2:end-1,1:end-2])-
dt/dy*vn[2:end-1,2:end-1].*(vn[2:end-1,2:end-1]-vn[1:end-2,2:end-1])+
nu*dt/dx^2*(vn[2:end-1,3:end]-2*vn[2:end-1,2:end-1]+vn[2:end-1,1:end-2])+
nu*dt/dy^2*(vn[3:end,2:end-1]-2*vn[2:end-1,2:end-1]+vn[3:end,2:end-1])
 
   u[1,:] .= 1
   u[end,:] .= 1
   u[:,1] .= 1
   u[:,end] .= 1
 
   v[1,:] .= 1
   v[end,:] .= 1
   v[:,1] .= 1
   v[:,end] .= 1

显示最终结果。

fig = PyPlot.figure(figsize=(11,7), dpi=100)
wire1 = PyPlot.plot_wireframe(x,y,u,color="b")
# fig2=PyPlot.figure(figsize=(11,7),dpi=100)
# wire2 = PyPlot.plot_wireframe(x,y,v,color="k")
PyPlot.xlabel("x(m)")
PyPlot.ylabel("y(m)")
PyPlot.zlabel("u(m/s)")
PyPlot.show()

最终分布如下图所示。

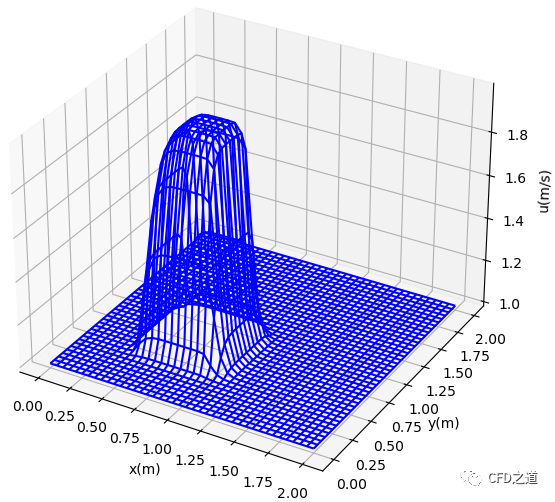
完整代码如下所示。

using PyPlot
matplotlib.use("TkAgg")
 
nx = 41
ny = 41
nt = 120
c = 1
dx = 2 / (nx - 1)
dy = 2 / (ny - 1)
sigma = 0.0009
nu = 0.01
dt = sigma * dx * dy / nu;
 
x = range(0, 2, length = nx)
y = range(0, 2, length = ny)
 
u = ones((ny, nx))
v = ones((ny, nx))
comb = ones((ny, nx))
 
# 初始条件
u[floor(Int, 0.5 / dy):floor(Int, 1 / dy),floor(Int, 0.5 / dx):floor(Int, 1 / dx),] .= 2
v[floor(Int, 0.5 / dy):floor(Int, 1 / dy),floor(Int, 0.5 / dx):floor(Int, 1 / dx),] .= 2
 
# PyPlot.plot_wireframe(x,y,u,cmap=ColorMap("coolwarm"))
# PyPlot.show()
 
for n in 1:nt
    un =copy(u)
    vn =copy(v)
    u[2:end-1,2:end-1] = un[2:end-1,2:end-1] - dt/dx*un[2:end-1,2:end-1].*(un[2:end-1,2:end-1]-un[2:end-1,1:end-2])-
dt/dy*vn[2:end-1,2:end-1].*(un[2:end-1,2:end-1]-un[1:end-2,2:end-1])+
nu*dt/dx^2*(un[2:end-1,3:end]-2*un[2:end-1,2:end-1]+un[2:end-1,1:end-2])+
nu*dt/dy^2*(un[3:end,2:end-1]-2*un[2:end-1,2:end-1]+un[3:end,2:end-1])
 
   v[2:end-1,2:end-1] = vn[2:end-1,2:end-1] - dt/dx*un[2:end-1,2:end-1].*(vn[2:end-1,2:end-1]-vn[2:end-1,1:end-2])-
dt/dy*vn[2:end-1,2:end-1].*(vn[2:end-1,2:end-1]-vn[1:end-2,2:end-1])+
nu*dt/dx^2*(vn[2:end-1,3:end]-2*vn[2:end-1,2:end-1]+vn[2:end-1,1:end-2])+
nu*dt/dy^2*(vn[3:end,2:end-1]-2*vn[2:end-1,2:end-1]+vn[3:end,2:end-1])
 
   u[1,:] .= 1
   u[end,:] .= 1
   u[:,1] .= 1
   u[:,end] .= 1
 
   v[1,:] .= 1
   v[end,:] .= 1
   v[:,1] .= 1
   v[:,end] .= 1
end
 
fig = PyPlot.figure(figsize=(11,7), dpi=100)
wire1 = PyPlot.plot_wireframe(x,y,u,color="b")
# fig2=PyPlot.figure(figsize=(11,7),dpi=100)
# wire2 = PyPlot.plot_wireframe(x,y,v,color="k")
PyPlot.xlabel("x(m)")
PyPlot.ylabel("y(m)")
PyPlot.zlabel("u(m/s)")
PyPlot.show()