二维扩散问题控制方程可写出下面形式:
这里时间项采用向前差分,空间项均采用中心差分,很容易写出离散方程:
同样写出待求项:
初始条件及边界条件见代码。
using PyPlot
nx = 101
ny = 101
nu = 0.2
dx = 2 / (nx - 1)
dy = 2 / (ny - 1)
sigma = 0.25
dt = sigma * dx * dy / nu
x = range(0, 2, length=nx)
y = range(0, 2, length=ny)
u = ones(ny, nx)
un = ones(ny, nx)
# 初始化
u[floor(Int, 0.5 / dy):floor(Int, 1 / dy),floor(Int, 0.5 / dx):floor(Int, 1 / dx)] .= 2
# 绘制初始值
PyPlot.surf(x,y,u)
xlim(0,2)
ylim(0,2)
zlim(1,2.5)
PyPlot.show()
初始条件如下图所示。
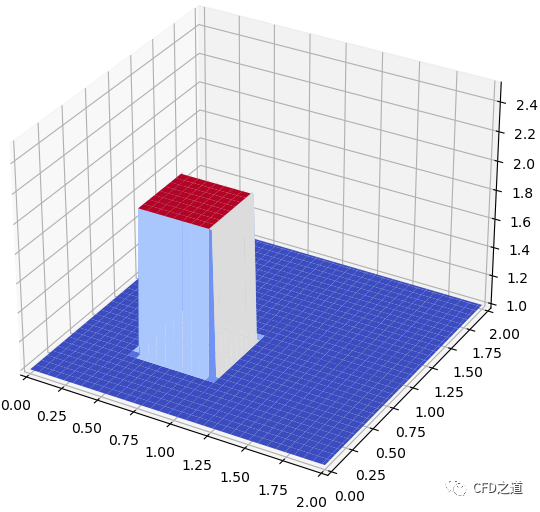
下面定义函数进行求解。
function diffuse(nt)
for n in 1:nt
PyPlot.cla()
un = copy(u)
u[2:end - 1,2:end - 1] = un[2:end - 1,2:end - 1] + nu * dt / dx^2 * (un[2:end - 1,3:end] - 2 * un[2:end - 1,2:end - 1] + un[2:end - 1,1:end - 2]) + nu * dt / dy^2 * (un[3:end,2:end - 1] - 2 * un[2:end - 1,2:end - 1] + un[1:end - 2,2:end - 1])
u[1,:] .= 1
u[end,:] .= 1
u[:,1] .= 1
u[1,end] = 1
end
PyPlot.surf(x, y, u, cmap=ColorMap("coolwarm"))
PyPlot.xlim(0, 2)
PyPlot.ylim(0, 2)
PyPlot.zlim(1, 2.5)
PyPlot.title(@sprintf("Timestep:%d",nt))
PyPlot.pause(.2)
PyPlot.show()
end
下面进行计算。
diffuse(300)
图形如下图所示。
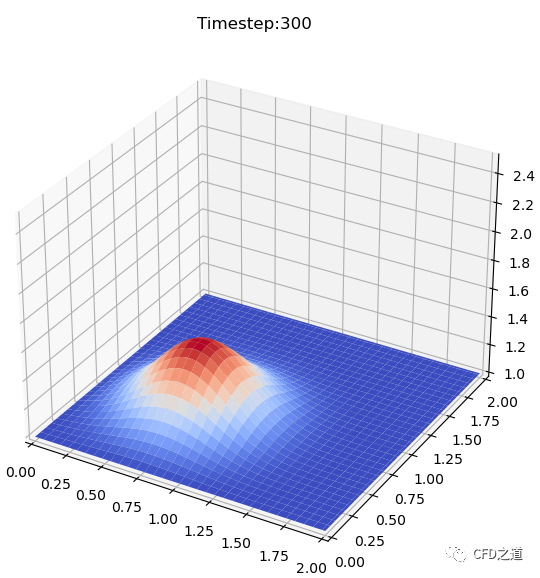
改造成以下的完整代码以动画形式显示扩散过程。
using PyPlot
using Printf
nx = 101
ny = 101
nu = 0.2
dx = 2 / (nx - 1)
dy = 2 / (ny - 1)
sigma = 0.25
dt = sigma * dx * dy / nu
x = range(0, 2, length=nx)
y = range(0, 2, length=ny)
u = ones(ny, nx)
u[floor(Int, 0.5 / dy):floor(Int, 1 / dy),floor(Int, 0.5 / dx):floor(Int, 1 / dx)] .= 2
# 显示初始条件
# PyPlot.surf(x,y,u)
# xlim(0,2)
# ylim(0,2)
# zlim(1,2.5)
# PyPlot.show()
function diffuse(nt)
for n in 1:nt
PyPlot.cla()
un = copy(u)
u[2:end - 1,2:end - 1] = un[2:end - 1,2:end - 1] + nu * dt / dx^2 * (un[2:end - 1,3:end] - 2 * un[2:end - 1,2:end - 1] + un[2:end - 1,1:end - 2]) + nu * dt / dy^2 * (un[3:end,2:end - 1] - 2 * un[2:end - 1,2:end - 1] + un[1:end - 2,2:end - 1])
u[1,:] .= 1
u[end,:] .= 1
u[:,1] .= 1
u[1,end] = 1
PyPlot.surf(x, y, u, cmap=ColorMap("coolwarm"))
PyPlot.xlim(0, 2)
PyPlot.ylim(0, 2)
PyPlot.zlim(1, 2.5)
PyPlot.title(@sprintf("Timestep:%d",n))
PyPlot.pause(.2)
end
PyPlot.show()
end
diffuse(300)
计算结果如下图所示。
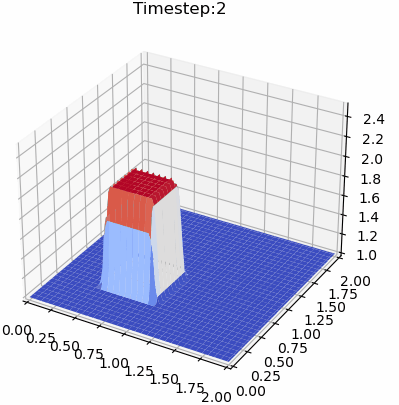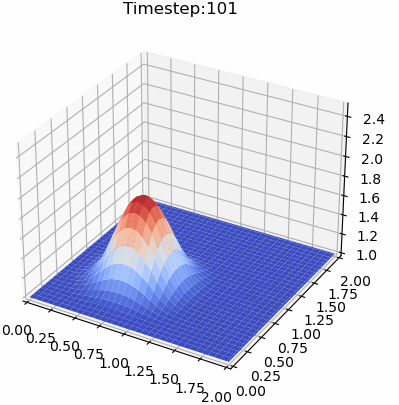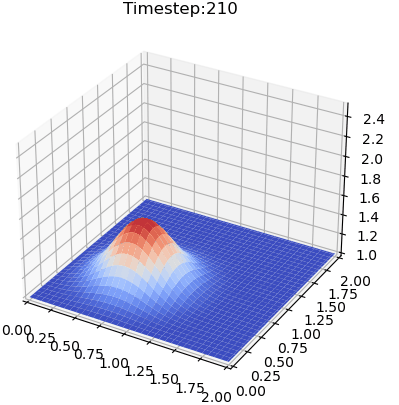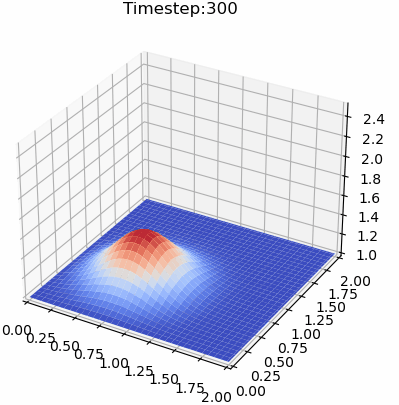
本篇文章来源于微信公众号: CFD之道








评论前必须登录!
注册