本文描述利用Julia计算二维非线性对流问题。

二维非线性对流控制方程为：

这里时间项采用向前差分，空间项采用向后差分，离散方程可写成以下格式：

式中，i为x方向角标，j为y方向角标，n为时间项角标。

可得待求项：

采用初始条件：

边界条件：

程序代码

using PyPlot
nx = 101
ny = 101
nt = 80
c = 1
dx = 2 / (nx - 1)
dy = 2 / (ny - 1)
sigma = 0.2
dt = sigma * dx
 
x = range(0, 2, length=nx)
y = range(0, 2, length=ny)
 
u = ones(ny, nx)
v = ones(ny, nx)
un = ones(ny, nx)
vn = ones(ny, nx)
 
s = floor(Int, 0.5 / dy)
e = floor(Int, 1 / dy)
u[s:e,s:e] .= 2
v[s:e,s:e] .= 2

显示初始化分布。

PyPlot.surf(x,y,u,cmap=ColorMap("coolwarm"))
PyPlot.show()

初始化分布如下图所示。

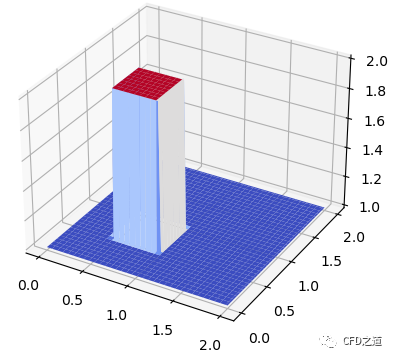
进行迭代计算。

for n in 1:nt
    un = copy(u)
    vn = copy(v)
    u[2:end,2:end] = un[2:end,2:end] - (un[2:end,2:end] .* (c * dt / dx * (un[2:end,2:end] - un[2:end,1:end - 1]))) - (vn[2:end,2:end] .* (c * dt / dy * (un[2:end,2:end] - un[1:end - 1,2:end])))
    v[2:end,2:end] = vn[2:end,2:end] - (un[2:end,2:end] .* (c * dt / dx * (vn[2:end,2:end] - vn[2:end,1:end - 1]))) - (vn[2:end,2:end] .* (c * dt / dy * (vn[2:end,2:end] - vn[1:end - 1,2:end])))
 
    u[1,:] .= 1;
    u[end,:] .= 1;
    u[:,1] .= 1;
    u[:,end] .= 1;
 
    v[1,:] .= 1;
    v[end,:] .= 1;
    v[:,1] .= 1;
    v[:,end] .= 1;
end
 
fig = figure(figsize=(11, 7), dpi=100)        
PyPlot.surf(x,y,u,cmap=ColorMap("coolwarm"))
PyPlot.show()

计算结果显示。

• x方向速度分布

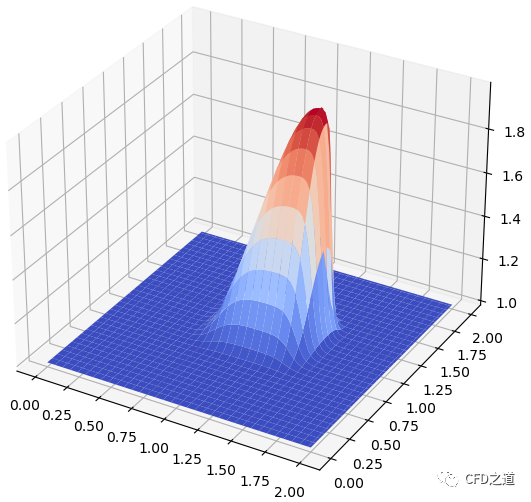
• y方向速度分布

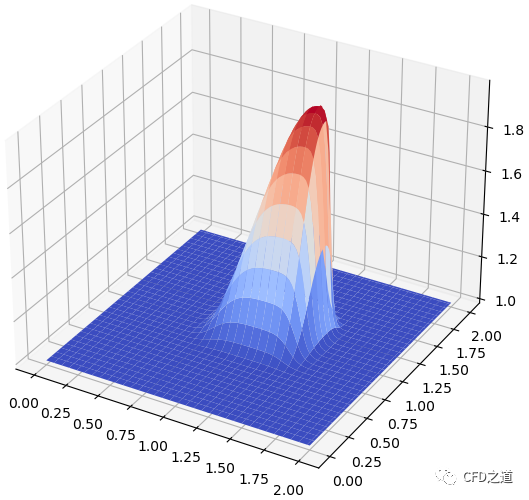
完整代码如下所示。

using PyPlot
nx = 101
ny = 101
nt = 80
c = 1
dx = 2 / (nx - 1)
dy = 2 / (ny - 1)
sigma = 0.2
dt = sigma * dx
 
x = range(0, 2, length=nx)
y = range(0, 2, length=ny)
 
u = ones(ny, nx)
v = ones(ny, nx)
un = ones(ny, nx)
vn = ones(ny, nx)
 
s = floor(Int, 0.5 / dy)
e = floor(Int, 1 / dy)
u[s:e,s:e] .= 2
v[s:e,s:e] .= 2
 
# PyPlot.surf(x,y,u,cmap=ColorMap("coolwarm"))
# PyPlot.show()
 
for n in 1:nt
    un = copy(u)
    vn = copy(v)
    u[2:end,2:end] = un[2:end,2:end] - (un[2:end,2:end] .* (c * dt / dx * (un[2:end,2:end] - un[2:end,1:end - 1]))) - (vn[2:end,2:end] .* (c * dt / dy * (un[2:end,2:end] - un[1:end - 1,2:end])))
    v[2:end,2:end] = vn[2:end,2:end] - (un[2:end,2:end] .* (c * dt / dx * (vn[2:end,2:end] - vn[2:end,1:end - 1]))) - (vn[2:end,2:end] .* (c * dt / dy * (vn[2:end,2:end] - vn[1:end - 1,2:end])))
 
    u[1,:] .= 1;
    u[end,:] .= 1;
    u[:,1] .= 1;
    u[:,end] .= 1;
 
    v[1,:] .= 1;
    v[end,:] .= 1;
    v[:,1] .= 1;
    v[:,end] .= 1;
end
 
fig = figure(figsize=(11, 7), dpi=100)        
PyPlot.surf(x,y,u,cmap=ColorMap("coolwarm"))
PyPlot.show()