一维非线性对流问题的控制方程为:
采用时间向前空间向后差分格式进行离散,其离散方程为:
改写为迭代形式为:
注:
此处的离散格式为显式,也可以尝试改成其它差分格式(如时间向后、空间向前、中心差分等)进行离散。若采用隐式方式可能会涉及到代数方程的组装与求解。
”
代码如下所示。
using PyPlot
using Printf
nx = 41;
dx = 2 / (nx - 1);
nt = 25;
dt = 0.025;
c = 1;
u = ones(nx);
s = Int(0.5 / dx);
e = Int(1 / dx);
u[s:e] .= 2;
un = ones(nx)
for n in 1:nt
PyPlot.cla()
un = copy(u)
for i in 2:nx
u[i] = un[i] - un[i] * dt / dx * (un[i] - un[i - 1])
end
plot(range(0, stop=2, length=nx), u, color="red", linewidth=2)
PyPlot.title(@sprintf("times=%.3f s", n * dt))
PyPlot.pause(.2)
end
PyPlot.show()
计算结果如下图所示。
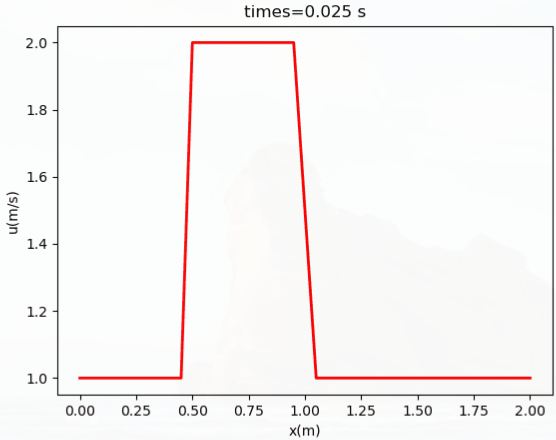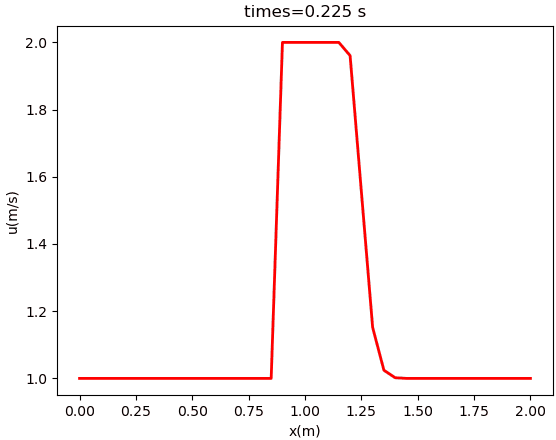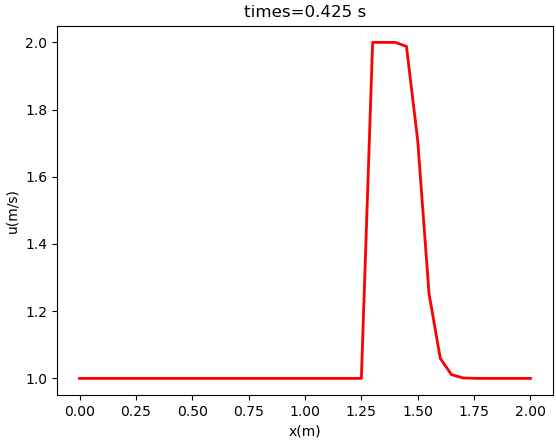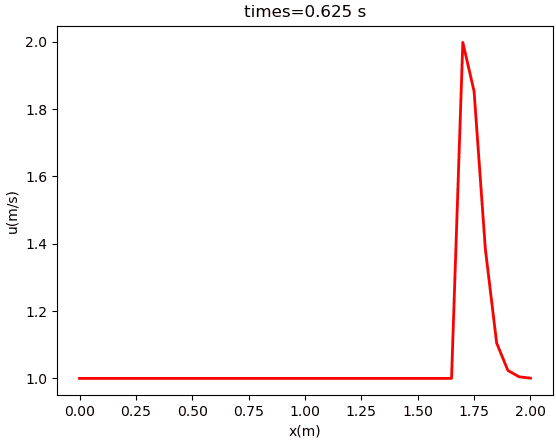
本篇文章来源于微信公众号: CFD之道








评论前必须登录!
注册