Julia CFD｜01 一维线性对流

一维线性对流问题的控制方程为：

对该控制方程时间项采用向前差分，对流项采用向后差分，控制方程可离散为以下形式：

写成迭代形式为：

利用Julia进行计算，代码如下所示。

# 使用PyPlot模块进行图形绘制，这个模块不是Julia的内置模块，需要额外安装
# PyPlot模块实质上是Matplotlib.PyPlot的Julia封装
using PyPlot
 
# 网格节点数量为41，将空间域等分为40等份
nx = 41;
# 空间计算域范围为0~2，dx为网格间距
dx = 2 / (nx - 1);
# 时间步数25步
nt = 25;
# 时间步长0.025s，总计算时间为0.625s
dt = 0.025;
 
# 常数c=1
c = 1;
 
# 构造初始条件
u = ones(nx);
s = Int(0.5 / dx);
e = Int(1 / dx);
u[s:e] .= 2;
 
# 绘制初始条件
PyPlot.plot(range(0.0, stop=2, length=nx),u,color="blue",linewidth=2.0,label="Time=0s")
 
# 构造un数组作为临时数组
un = ones(nx);
# 利用离散式进行迭代计算
for n in 1:nt
    un = copy(u)
    for i in 2:nx
        u[i] = un[i] - c * dt / dx * (un[i] - un[i - 1])
    end
end
 
# 绘制结果数据
PyPlot.plot(range(0, 2, length=nx),u,color="red",linewidth=2.0,label="Time = 0.625s")
PyPlot.xlabel("x(m)")
PyPlot.ylabel("velocity(m/s)")
PyPlot.legend(loc=1)
# PyPlot.grid()
PyPlot.show()

计算结果如下图所示。

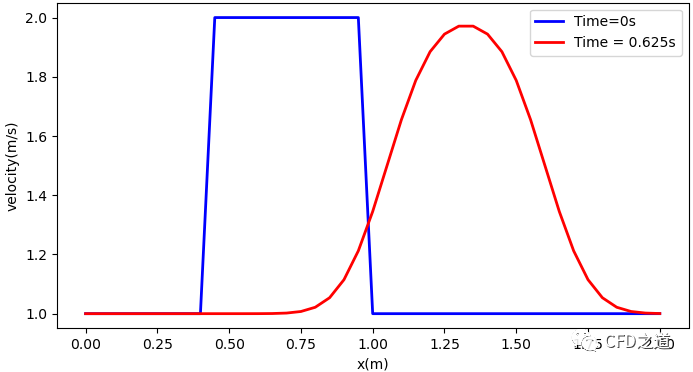
发现经过0.625 s后，波形发生了失真，在一定程度上我们可以通过加密计算网格或减小时间步长来进行改善。

如保持时间步长不变，增大网格节点数为81时，计算结果如下图所示。

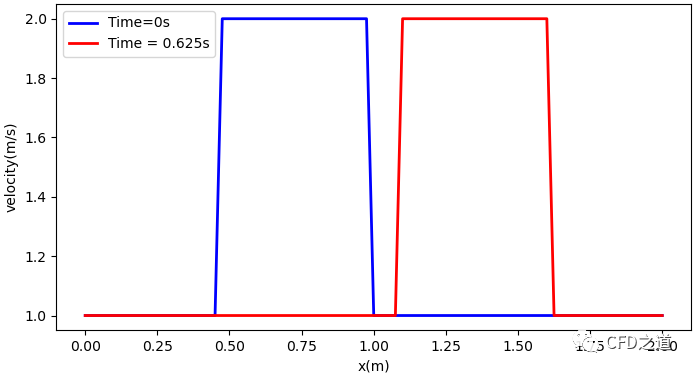
不过当网格加密到一定程度后，若时间步长依然不变的话，计算过程会崩溃。如将网格节点数增加到101时，计算结果如下图所示。

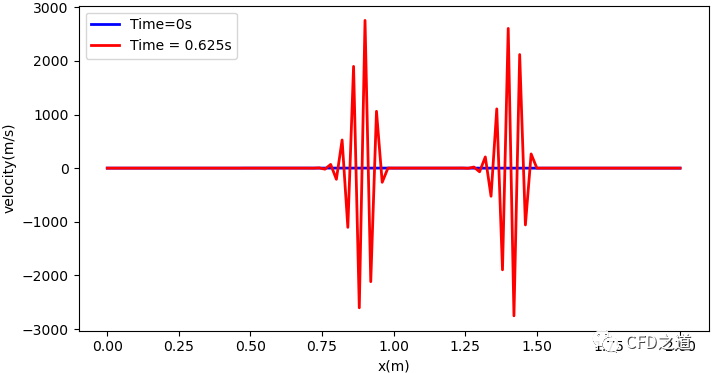
可以看到计算完全失真。这里涉及到计算条件收敛的问题，留在后续再讨论。

注：

实际上在一些成熟商业CFD软件计算过程中偶尔也会出现此类问题，稀疏网格能收敛加密网格反而发散。

”

前面的离散采用的是显式格式，事实上也可以采用隐式方式进行离散，这部分内容留待后续进行介绍。

改造成可视版本代码，如下所示。

using PyPlot
using Printf
 
# 网格节点数量为41，将空间域等分为40等份
nx = 81;
# 空间计算域范围为0~2，dx为网格间距
dx = 2 / (nx - 1);
# 时间步数25步
nt = 25;
# 时间步长0.025s，总计算时间为0.625s
dt = 0.025;
 
# 常数c=1
c = 1;
 
# 构造初始条件
u = ones(nx);
s = Int(0.5 / dx);
e = Int(1 / dx);
u[s:e] .= 2;
 
# 利用离散式进行迭代计算
for n = 1:nt
    PyPlot.cla()
    un = copy(u)
    u[2:end] = un[2:end] - c * dt / dx * (un[2:end] - un[1:end-1])
 
    # 绘制结果数据
    plot(
        range(0, 2, length = nx),
        u,
        color = "red",
        linewidth = 2.0,
        label = @sprintf("Time = %.4fs", n * dt),
    )
    xlabel("x(m)")
    ylabel("velocity(m/s)")
    legend(loc = 1)
    pause(0.2)
end
 
PyPlot.show()

图形如下图所示。