本算例利用OpenFOAM计算旋转腔体内速度分布，并对计算结果进行验证。

参考文献：J.A. Michelsen. “Modeling of Laminar Incompressible Rotating Fluid Flow”. AFM 86-05., Ph.D. thesis. Department of Fluid Mechanics, Technical University of Denmark. 1986.

”

本案例主要演示旋转边界的设置。

1 案例描述

本算例几何如图所示。

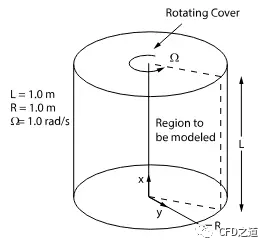
圆柱形封闭腔体底面半径1m，高度1m，其顶盖以角速度1rad/s旋转。腔体中介质密度1 kg/m3，动力粘度0.000556 kg/m-s，计算分析半径0.6m圆柱面上径向速度分布。

2 OpenFOAM设置

2.1 文件准备

本算例为层流计算，选择simpleFoam中的pitzDaily作为模板算例。打开终端进入到算例路径下，并采用下面的命令准备文件。

cp -r $FOAM_TUTORIALS/incompressible/simpleFoam/pitzDaily .
mv pitzDaily VM08
cd VM08

删除多余的文件，最终算例文件夹组织结构如下所示。

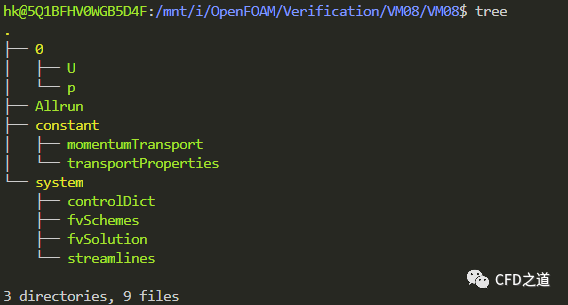
2.2 计算网格

在ICEM CFD中生成三维计算网格。

• 将网格文件拷贝到工作路径下，并运行下面的命令转换计算网格

fluentMeshToFoam VM08.msh

转换完毕后的boundary文件内容如下所示。

FoamFile
{
    version     2.0;
    format      ascii;
    class       polyBoundaryMesh;
    location    "constant/polyMesh";
    object      boundary;
}
// * * * * * * * * * * * * * //
 
3
(
    TOP
    {
        type            wall;
        inGroups        List 1(wall);
        nFaces          2560;
        startFace       149760;
    }
    CYLINDER
    {
        type            wall;
        inGroups        List 1(wall);
        nFaces          2560;
        startFace       152320;
    }
    BOTTOM
    {
        type            wall;
        inGroups        List 1(wall);
        nFaces          2560;
        startFace       154880;
    }
)

• 转换完毕后运行命令checkMesh检查网格，确保计算网格没有问题

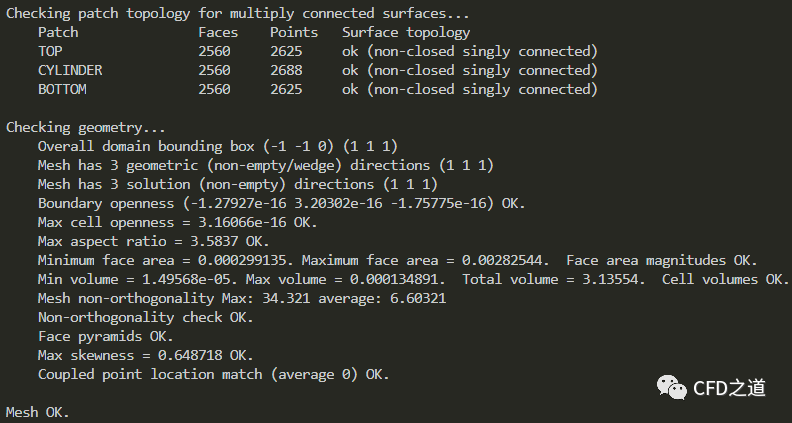
2.3 设置模型与介质属性

• 修改constant/momentumTransport文件，使用层流模型进行计算

FoamFile
{
    version     2.0;
    format      ascii;
    class       dictionary;
    location    "constant";
    object      momentumTransport;
}
// * * * * * * * * * * * * * * * * *
simulationType laminar;

• 修改transportProperties文件，指定运动粘度

FoamFile
{
    version     2.0;
    format      ascii;
    class       dictionary;
    location    "constant";
    object      transportProperties;
}
// * * * * * * * * * * * * * * * * * * //
transportModel  Newtonian;
nu              [0 2 -1 0 0 0 0] 0.000556;

2.4 指定边界条件

1、p文件

p文件内容如下所示。

FoamFile
{
    version     2.0;
    format      ascii;
    class       volScalarField;
    object      p;
}
// * * * * * * * * * * * * * * * * * //
 
dimensions      [0 2 -2 0 0 0 0];
 
internalField   uniform 0;
 
boundaryField
{
    "(TOP|BOTTOM|CYLINDER)"
    {
        type            zeroGradient;
    }
}

1、U文件

U文件内容如下所示。

FoamFile
{
    version     2.0;
    format      ascii;
    class       volVectorField;
    object      U;
}
// * * * * * * * * * * * * //
 
dimensions      [0 1 -1 0 0 0 0];
 
internalField   uniform (0 0 0);
 
boundaryField
{
    TOP
    {
        type            rotatingWallVelocity;
        origin          (0 0 1);
        axis            (0 0 1);
        omega           1;
 
    }
 
    "(CYLINDER|BOTTOM)"
    {
        type            noSlip;
    }
 
}

2.5 设置控制条件

1、controlDict文件

FoamFile
{
    version     2.0;
    format      ascii;
    class       dictionary;
    location    "system";
    object      controlDict;
}
// * * * * * * * * * * * * * * * * //
application     simpleFoam;
startFrom       startTime;
startTime       0;
stopAt          endTime;
endTime         2000;
deltaT          1;
writeControl    timeStep;
writeInterval   100;
purgeWrite      2;
writeFormat     ascii;
writePrecision  6;
writeCompression off;
timeFormat      general;
timePrecision   6;
runTimeModifiable true;

2、fvSolution文件

FoamFile
{
    version     2.0;
    format      ascii;
    class       dictionary;
    location    "system";
    object      fvSolution;
}
// * * * * * * * * * * * * * * * * //
solvers
{
    p
    {
        solver          GAMG;
        tolerance       1e-06;
        relTol          0.1;
        smoother        GaussSeidel;
    }
    "(U|k|epsilon|omega|f|v2)"
    {
        solver          smoothSolver;
        smoother        symGaussSeidel;
        tolerance       1e-06;
        relTol          0.1;
    }
}
 
SIMPLE
{
    nNonOrthogonalCorrectors 0;
    consistent      yes;
    residualControl
    {
        p               1e-6;
        U               1e-6;   
    }
    // 由于p方程中所有的边界条件均为zeroGradient
    // 因此这里需要设置压力参考值
    // 不设置的话会报错
    pRefCell        0;
    pRefValue       0;
}
relaxationFactors
{
    equations
    {
        U               0.9;
        ".*"            0.9;
    }
}

2.6 执行计算

若本机上安装了PyFoam的话，可以使用下面的命令在计算过程中显示残差。

pyFoamPlotRunner.py --clear simpleFoam

若没有安装PyFoam，则可以使用foamMonitor命令监控残差。

计算残差如下图所示，在282步达到收敛。

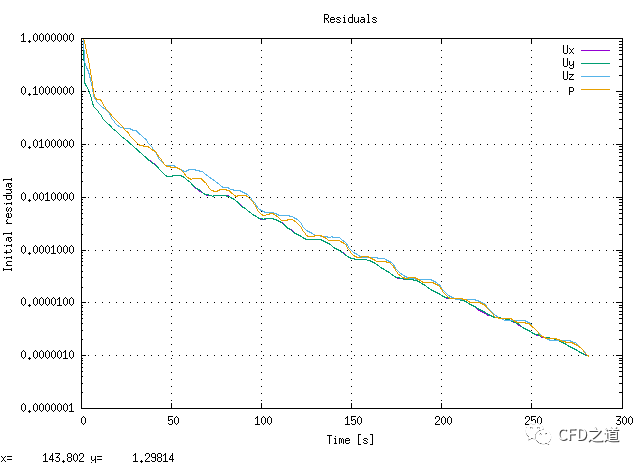
3 计算结果

• x=0.5m面上速度分布

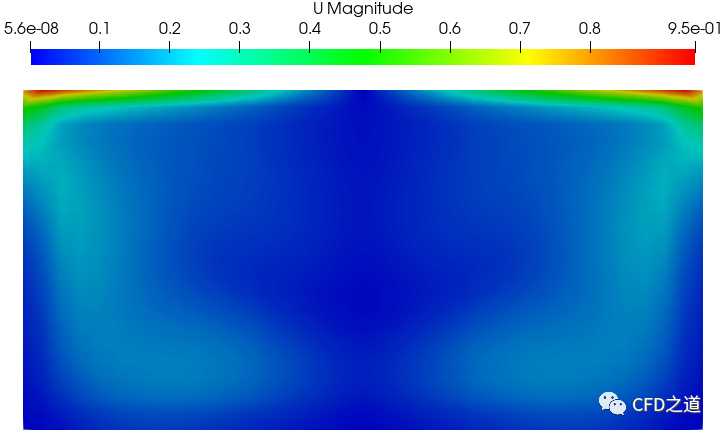
为了方便与实验值进行比较，这里在x=0.6 m面上取一条沿Z轴的线（两个点（0.6 0 0）→（0.6 0 1）所构成）。

• 选择按钮****

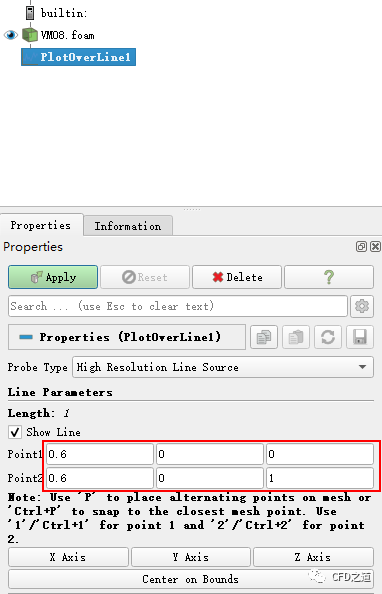
• 确保选中U_X及U_Y项。

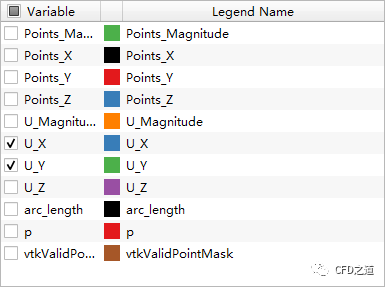
• 生成的曲线图如下图所示

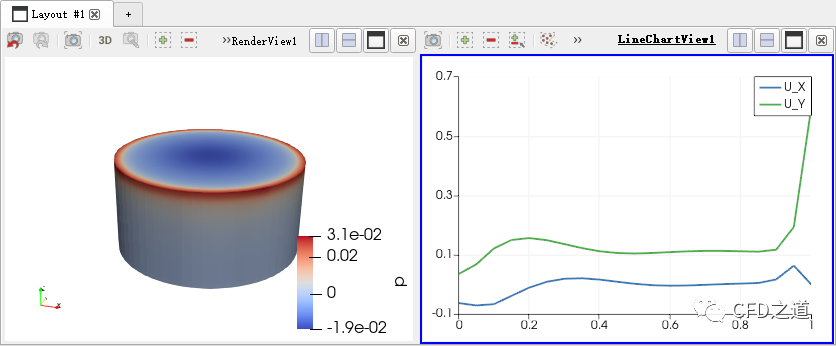
• 确保图形窗口中的曲线图被选中，利用菜单**File → Export Scene…**导出曲线上的数据，可以将其导出为csv或txt格式，方便后面使用gnuplot绘图

• x=0.6m处速度比较结果

set xrange [0.0:1.0]
set xlabel "x(m)"
set ylabel "velocity(m/s)"
set grid
set key bottom
plot "VM08.txt" u 1:2 w line lw 3 t "numeric","radial_exp.xy" u 1:2 w point pt 7 t "exp"

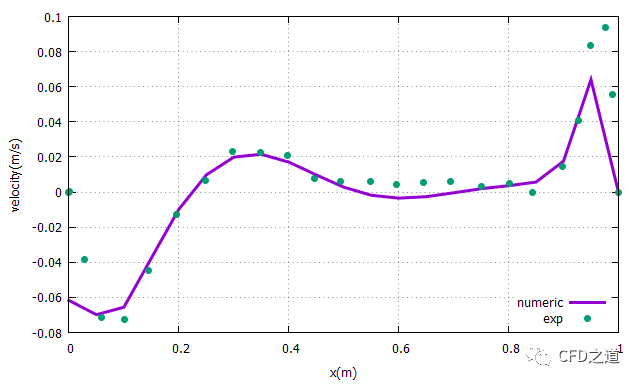
• x=0.6m位置切向速度比较结果

plot "VM08.txt" u 1:3 w line lw 3 t "numeric","swirl_exp.xy" u 1:2 w point pt 7 t "exp"

比较结果如下图所示。

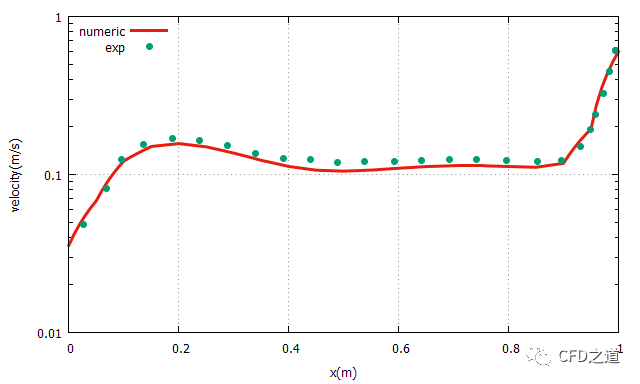
相关文件：