本案例利用OpenFOAM计算并验证管道内部泊肃叶流动产生的层流压降。

文献：F.M. White. Fluid Mechanics. 3rd Edition. McGraw-Hill Book Co., New York, NY. 1994.

”

1 案例描述

本案例计算管道内部泊肃叶流动压降。案例几何如图所示。

管道半径0.00125m，长度0.1m，内部介质密度1 kg/m3，粘度1e-5 kg/m-s。管内入口流动为充分发展层流，平均速度为2 m/s。

充分发展速度表达式为：

2 验证解

验证解析解来自F. M. White. Fluid Mechanics(7nd ed)，p357。

本案例雷诺数为：

泊肃叶流动摩擦系数：

可得压降：

采用2D轴对称模型进行计算。

3 OpenFOAM设置

案例采用simpleFoam求解器进行计算，网格采用msh文件导入。

3.1 文件准备

采用simpleFoam求解器中的pitzDaily算例作为模板。

• 进入算例目录，运行下面的命令准备文件

cp -r $FOAM_TUTORIALS/incompressible/simpleFoam/pitzDaily .
mv pitzDaily VM05
cd VM05

• 删除多余的文件

cd 0
rm epsilon f k nut nuTilda omega v2
cd ..

文件结构如下图所示。

3.2 准备网格

• 将网格文件VM05.msh拷贝到算例文件夹中
• 采用下面命令转换计算网格

fluentMeshToFoam VM05.msh

• 修改contant/polyMesh/boundary文件

FoamFile
{
    version     2.0;
    format      ascii;
    class       polyBoundaryMesh;
    location    "constant/polyMesh";
    object      boundary;
}
// * * * * * * * * * * * * * * * * * //
// 修改边界SIDE1与SIDE2为wedge
5
(
    INLET
    {
        type            patch;
        nFaces          20;
        startFace       31180;
    }
    SIDE1
    {
        type            wedge;
        inGroups        List 1(wall);
        nFaces          16000;
        startFace       31200;
    }
    OUTLET
    {
        type            patch;
        nFaces          20;
        startFace       47200;
    }
    WALL
    {
        type            wall;
        inGroups        List 1(wall);
        nFaces          800;
        startFace       47220;
    }
    SIDE2
    {
        type            wedge;
        inGroups        List 1(wall);
        nFaces          16000;
        startFace       48020;
    }
)

• 文件修改完毕后，运行命令checkMesh检查网格，确保没有任何错误或警告信息

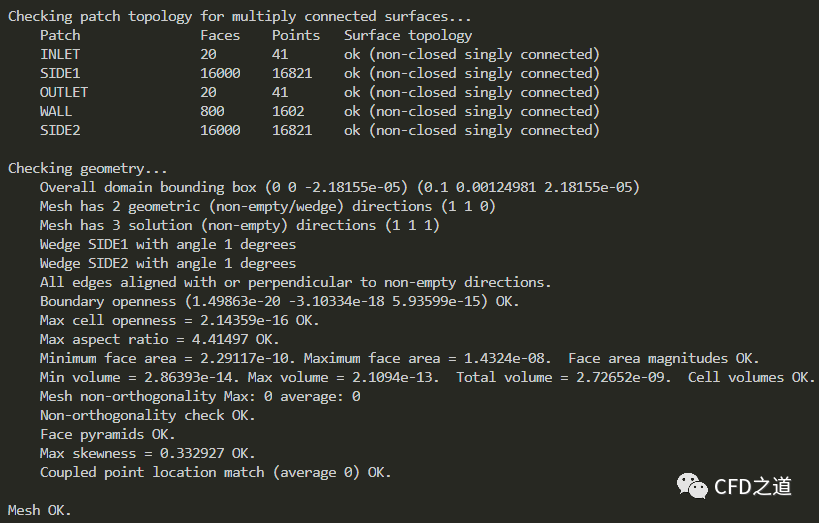
3.3 设置物性参数

1、transportProperties文件

如下图所示设置。

FoamFile
{
    version     2.0;
    format      ascii;
    class       dictionary;
    location    "constant";
    object      transportProperties;
}
// * * * * * * * * * * * * * * //
transportModel  Newtonian;
 
nu              [0 2 -1 0 0 0 0] 1e-05;

2、momentumTransport文件

采用层流计算，文件修改为：

FoamFile
{
    version     2.0;
    format      ascii;
    class       dictionary;
    location    "constant";
    object      momentumTransport;
}
// * * * * * * * * * * * * * * * * * //
 
simulationType Laminar;

3.4 边界条件设置

1、U文件

U文件中主要需要指定入口边界的充分发展流动，这里使用codeFixedValue来实现。

FoamFile
{
    version     2.0;
    format      ascii;
    class       volVectorField;
    object      U;
}
// * * * * * * * * * * * * * //
 
dimensions      [0 1 -1 0 0 0 0];
 
internalField   uniform (0 0 0);
 
boundaryField
{
    INLET
    {
        type            codedFixedValue;       
        value           uniform (2 0 0);
        name            parabolicVelocity;
        code
        #{
            // 下面三行为标准写法，一般不用修改
            const fvPatch& boundaryPatch = patch();
            const vectorField& Cf = boundaryPatch.Cf();
            vectorField& field = *this;
            // U_0为2倍的平均速度；p_ctr为中心点偏移量；p_r为半径
            scalar U_0 = 4, p_ctr = 0, p_r = 0.00125;
 
            forAll(Cf, faceI)
            {
                field[faceI] = vector(U_0*(1-(pow(Cf[faceI].y()-p_ctr,2))/(p_r*p_r)),0,0);
            }
        #};
 
    }
    SIDE1
    {
        type            wedge;
    }
    OUTLET
    {
        type            zeroGradient;
 
    }
    WALL
    {
        type            noSlip;
    }
    SIDE2
    {
        type            wedge;
    }
}

2、p文件

FoamFile
{
    version     2.0;
    format      ascii;
    class       volScalarField;
    object      p;
}
// * * * * * * * * * * * * * * //
 
dimensions      [0 2 -2 0 0 0 0];
 
internalField   uniform 0;
 
boundaryField
{
    INLET
    {
        type            zeroGradient;
 
    }
    SIDE1
    {
        type            wedge;
    }
    OUTLET
    {
        type            fixedValue;
        value           uniform 0;
 
    }
    WALL
    {
        type            zeroGradient;
    }
    SIDE2
    {
        type            wedge;
    }
}

3.5 求解控制

这里修改controlDic文件内容，如下所示。

FoamFile
{
    version     2.0;
    format      ascii;
    class       dictionary;
    location    "system";
    object      controlDict;
}
// * * * * * * * * * * * * * * * * // 
application     simpleFoam; 
startFrom       startTime; 
startTime       0; 
stopAt          endTime; 
endTime         2000; 
deltaT          1; 
writeControl    timeStep; 
writeInterval   100; 
purgeWrite      2; 
writeFormat     ascii; 
writePrecision  6; 
writeCompression off; 
timeFormat      general; 
timePrecision   6; 
runTimeModifiable true;

3.6 计算结果

• 速度分布

• 压力分布

• 定义入口压力

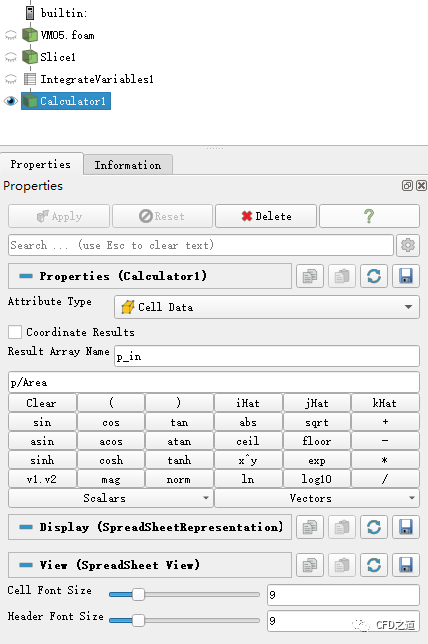
• 得到入口的运动压力

此处得到的压力值为运动压力，还需要乘上流体的密度才是正常的压力值。本算例中流体密度为1 kg/m3，因此可以得到管道的压力降为10.239 Pa。与公式计算得到的压力10.24 Pa相比，其相对误差为-0.0097%，几乎可以忽略。

相关文件：