本文简单描述OpenFOAM中的瞬态与稳态计算。

自然界和工业应用中，几乎所有流动问题都是非稳态的（也称为瞬态或时间依赖）。非稳定的原因可能来自于：流动非稳定性、非平衡的初始条件、时间相关的边界条件、源项、化学反应和有限速率化学、相变、运动或变形的固体、湍流、浮力和传热、不连续性、多相流、流固耦合、燃烧等。

1 瞬态模拟

在OpenFOAM中进行瞬态模拟，需要进行以下设置：

• 选择时间步。时间步的选择必须能够解决与时间有关的问题特征并保持求解器的稳定性。
• 选择时间离散格式。
• 设置线性求解器的残差（绝对残差和/或相对残差）。
• 监视CFL数。
• 监视求解的稳定性和有界性。
• 监控感兴趣物理量。
• 指定计算结果的保存频率，需要注意的是瞬态计算会生成大量数据。
• 指定计算的结束时间。
• 在controlDict字典中，需要设置运行时参数和有关如何运行算例的常规说明（例如时间步长和最大CFL数量）
• 在fvSchemes字典中，需要设置时间离散方案。
• 在fvSolution字典中，需要设置线性求解器。
• 若使用了PISO或PIMPLE方法，还需要在fvSolution字典中设置使用的速度-压力耦合方法的校正次数。
• 可以在controlDict词典中设置functionObjects。在运行模拟时，使用functionObjects进行采样及数据处理

1.2 fvSchemes设置

瞬态模拟需要在fvSchemes字典文件中指定ddtSchemes关键字。如下所示的字典文件示例：

ddtSchemes
{
    default backward;
}
gradSchemes
{
    default  Gauss linear;
    grad(p)         Gauss linear;
}
divSchemes
{
    default  none;
    div(phi,U)      Gauss linear;
}
laplacianSchemes
{
    default Gauss linear orthogonal;
}
interpolationSchemes
{
    default linear;
}
snGradSchemes
{
    default orthogonal;
}

如此示例中指定的ddtSchemes为backward方法，此方法为二阶精度算法，计算过程中存在振荡。

1.3 时间参数设置

瞬态模拟中与时间相关的参数需要在controlDict字典文件中进行指定。如下示例：

startFrom       latestTime;
// 指定时刻为0 s
startTime       0;
stopAt          endTime;
// 指定终止时刻为10 s
endTime         10;
// 指定时间步长0.0001 s
deltaT          0.0001;
writeControl    runTime;
// 指定文件写入间隔0.1 s
writeInterval   0.1;
// 保持算例路径不变
purgeWrite      0;
// 文件保存格式为ascii
writeFormat     ascii;
writePrecision  8;
writeCompression off;
timeFormat      general;
timePrecision   6;
runTimeModifiable  yes;
// 设置时间步长可调整，仅用于PIMPLE
adjustTimeStep   yes;
// 设置最大库朗数2.0
maxCo            2.0;
// 指定最大时间步长0.001 s
maxDeltaT        0.001;

1.4 线性算法设置

瞬态计算中在字典fvSolution中指定线性方程求解算法。如下面的字典示例：

solvers
{
    p
    {
        solver           PCG;
        preconditioner   DIC;
        tolerance        1e-06;
        relTol           0;
    }
    pFinal
    {
        $p;
        relTol    0;
    }
    “U.*”
    {
        solver           smoothSolver;
        smoother         symGaussSeidel;
        tolerance        1e-08;
        relTol           0;
    }
} 
// 需要定义子字典PISO或PIMPLE，取决于选用的求解器
PIMPLE
{
    // 设置此参数为1时等同于PISO算法
    // 增大此参数有助于提高稳定性
    // 大时间步长计算时建议增大此参数
    nOuterCorrectors 1;
    // 若使用大的时间步长导致CFL数远大于1
    // 建议设置nCorrectors大于3
    // 此参数至少为1，增大此参数会增大计算量
    nCorrectors    2;
    nNonOrthogonalCorrectors    1;
}

1.5 时间步长

在运行瞬态仿真时必须选择合适的时间步长，这样才能捕捉与时间有关的物理特征并保证求解器过程稳定。

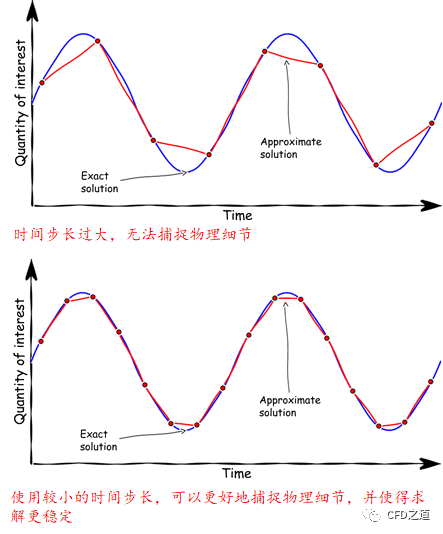
在进行瞬态模拟时，强烈建议监测感兴趣的物理量。这些物理量可能是随时间波动的，表面其具有时间依赖性。

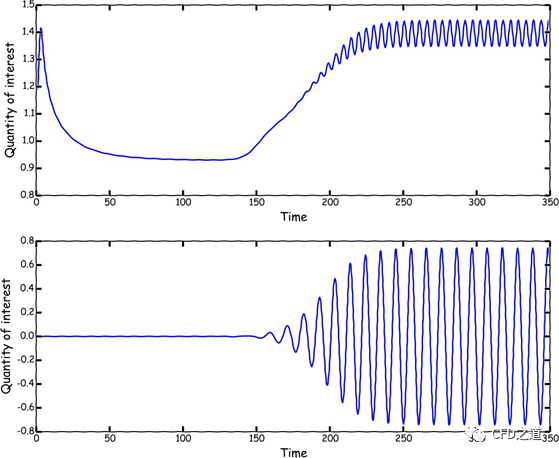
2 稳态模拟

稳态模拟是对现实世界的极大简化。稳态模拟是CFDer使用的一种技巧，目的是快速获得结果。不过需要切记的是，工程中遇到的绝大多数流动问题都是非稳态的。稳态模拟的最大优势在于它们需要的计算资源较少，更容易进行后处理和时间分析。

要进行稳态计算，需要选用适当的求解器和正确的离散格式。由于稳态模拟不求解时间导数，因此在计算过程中不需要设置时间步长，但是需要告诉OpenFOAM希望执行多少次迭代计算，还可以在fvSolution字典文件的SIMPLE子字典中设置残差控制(residualControl)参数。如果没有设置残差控制参数，OpenFOAM将一直运行直到达到最大迭代次数(endTime)。

2.1 OpenFOAM中稳态模拟

在OpenFOAM中进行稳态模拟，需要进行下面的设置：

• 在controlDict字典中，需要设置运行时参数和有关如何运行算例的一般指令(例如要执行的迭代次数)
• 设置数据保存的频率
• 在fvSchemes字典中，需要设置时间离散化方案，对于稳定的模拟，它必须是steadyState
• 在fvSolution字典中设置线性求解器、亚松弛因子及残差控制
• 需要在fvSolution字典中设置速度-压力耦合方法的校正次数(例如SIMPLEC或SIMPLEC)
• 可以在controlDict字典中设置functionObjects，用于在模拟运行时进行采样、探测和数据处理

2.2 fvSchemes字典

在稳态模拟时，需要在fvSchemes文件中指定时间项离散方法为steadyState。如下面的字典示例：

// 指定ddtSchemes为steadyState
// 表示采用稳态计算
ddtSchemes
{
    default steadyState;
}
gradSchemes
{
    default  Gauss linear;
    grad(p)         Gauss linear;
}
divSchemes
{
    default  none;
    // 稳态计算时常选择bounded Gauss linear
    div(phi,U)     bounded Gauss linear;
}
laplacianSchemes
{
    default Gauss linear orthogonal;
}
interpolationSchemes
{
    default linear;
}
snGradSchemes
{
    default orthogonal;
}

2.3 controlDict字典

除了需要在fvSchemes字典中设置离散方法外，稳态求解还需要在controlDict字典中指定迭代参数。如下面的字典示例，注意在稳态计算时controlDict字典中设置的时间并非真实的时间。

startFrom       latestTime;
// 从0步开始
startTime       0;
stopAt          endTime;
// 迭代计算10000次
endTime         10000;
// deltaT设置为1
deltaT          1;
writeControl    runTime;
// 间隔100次迭代保存一次结果文件
writeInterval   100;
// 保留最近的10个结果数据
purgeWrite      10;
writeFormat     ascii;
writePrecision  8;
writeCompression off;
timeFormat      general;
timePrecision   6;
runTimeModifiable  yes;

2.4 fvSolution字典

fvSolution字典指定如何求解每个离散化的线性方程组。如下字典示例：

solvers
{
    p
    {
        solver           PCG;
        preconditioner   DIC;
        tolerance        1e-06;
        relTol           0;
    }
    U
    {
        solver           smoothSolver;
        smoother         symGaussSeidel;
        tolerance        1e-08;
        relTol           0;
    }
} 
SIMPLE
{
    // 增加此参数值能提高稳定性，但会增大计算量
    nNonOrthogonalCorrectors    2;
    // 设置残差控制
    residualControl
    {
        p    1e-4;
        U    1e-4;
    }
}
// 设置亚松弛因子
relaxationFactors
{
    fields
    {
        p 0.3;
    }
    equations
    {
        U 0.7;
    }
}

2.5 亚松弛因子

亚松弛因子（under relaxation factor，URF）用于控制物理变量在迭代过程中的变化量：

利用SIMPLE方法求解稳态问题时常会使用到亚松弛因子，下面是在SIMPLE及SIMPLEC方法中常用的亚松弛因子组合：

// SIMPLE方法
p            0.3;
U            0.7;
k            0.7;
omega        0.7;
// SIMPLEC方法
p            1;   
U            0.9;
k            0.9;
omega        0.9;

根据所涉及的物理模型，可能需要添加更多的欠松弛因子。在实际应用过程中，选择合适的URF需要经验和一些试错性的工作。实际上选择URF相当于选择了正确的时间步长。有些时候稳态模拟会因为错误地选择URF而出现计算发散。

URF的取值范围为0~1，越接近于1收敛速度越快，但计算也更容易不稳定；反之URF越接近0收敛速度越慢，但计算越稳定。URF的最佳选择是足够小以保证计算稳定，足够大以加快迭代过程。

URF可以为隐式：

也可以为显式：

也可以将URF与CFL数合在一起使用：

小的CFL数等效于小的亚松弛因子。