本文简单介绍有限体积法（Finite Volume Method，FVM），并描述OpenFOAM应用过程中会接触到的一些基本概念。

注：本文内容整理自Wolf Dynamics公司公开的培训教材“A Crash Introduction to the Finite Volume Method and Discretization Schemes in OpenFOAM®”。本文为扫盲，更详细的内容可参阅教材《The Finite Volume Method in Computational Fluid Dynamics》，F. Moukalled, L. Mangani, M. Darwish。文中的公式很长，可以左右滑动查看完整的公式。

”

我们从通用输运方程开始描述FVM：

输运方程包含四大项，从左至右依次为：瞬态项、对流项、扩散项以及源项。从此方程出发，可以很容易写出NS方程的表达形式。CFD计算的目的是在给定边界条件与初始条件的情况下，求解出指定区域内通用输运方程的近似解。这是一个二阶方程，因此为了保证计算精度，有必要使离散方程在空间与时间上的阶次等于或高于方程的阶次，即离散方程在空间和时间上至少保证二阶精度。

1 区域离散

区域离散(或网格生成)在于将计算区域分割为有限数量的控制体或单元，如下图所示。

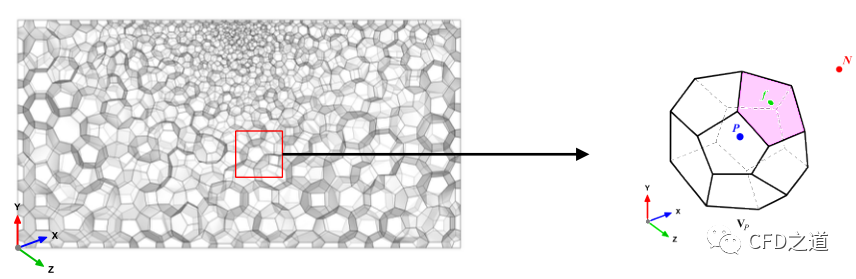
控制体的形状可以是任意的（如四面体、六面体、三棱柱、金字塔、多面体等），但围成这些控制体的面必须是平面。

如上图所示的控制体，其体中心及每个边界面的面心都是已知的。假设所有变量的值都被计算并存储在控制体的中心，且表示为：

此方式称之为体中心法。在有限体积法离散过程中，需要追踪大量的几何信息。

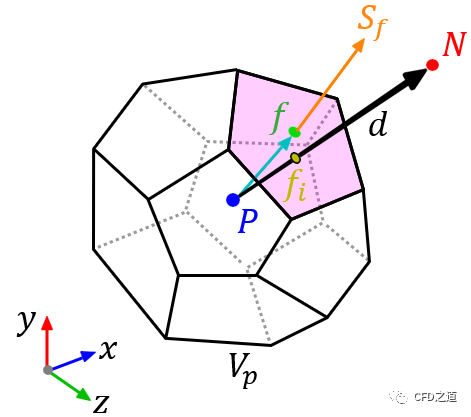
为便于后续描述，这里对于如下图所示的控制体做一些约定：

• 控制体围绕点而构造，其体积为，点为控制体的中心
• 从控制体的中心到相邻控制体的中心的向量命名为
• 控制体的所有相邻控制体都是已知的
• 控制体的边界面标记为，其也表示面中心
• 向量与面相交位置命名为
• 边界面的面积向量由控制体指向控制体外部，其位于面中心，沿面的法向方向，其幅值等于面的面积
• 从体心到面心的向量命名为

2 高斯散度定理

高斯散度定理描述为：

其中，为包围控制体的封闭曲面；为无穷小面单元；为指向面外部的面法向向量，且有。

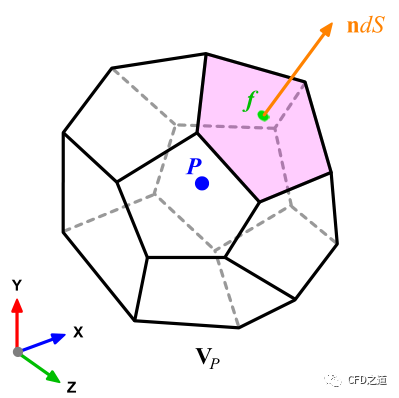
简单来讲，高斯散度定理描述为：矢量场的散度在体积D上的体积分等于矢量场在限定该体积的闭合曲面s上的面积分。高斯散度定理是FVM的基础，其用于将控制方程中出现的体积分转化为面积分。

对于通用控制方程：

可以通过高斯散度公式转化为：

此时问题转化为梯度项、跨越网格面上的扩散通量、对流项以及源项的离散。

对于对流项，利用高斯散度公式可以将体积分转化为：

对于扩散项，同样可以改写为：

对于梯度项，可以改写为：

对于源项，可以改写为：

式中，为源项中的常数项，为非线性项。

通过这样转换后，控制方程可转化为下面的形式：

其中，为扩散通量；为扩散通量。出现在对流通量与扩散通量中的面值必须由边界面两侧的控制体中心的变量值通过插值进行计算。

3 对流通量计算

控制体边界面上的对流通量值需要通过该面两侧的控制体中心变量插值计算。插值方法有很多，这里仅展示一些最常用的。

3.1 线性插值

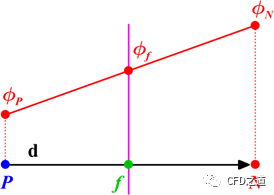
如下图所示，可以利用线性插值计算对流通量中的边界面上的值：

其中：

这种插值格式成为线性插值（linear interpolation）或中心差分（central differencing），其具有二阶精度。然而在一些工况下，此插值方式可能会产生求解振荡，其为无界格式。

3.2 一阶迎风格式

对流通量的面值计算还可以采用下面的方式：

这里的。

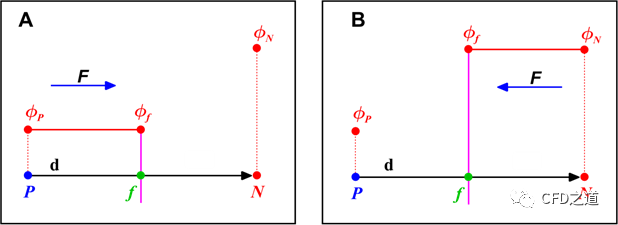
这种类型的插值方案被称为迎风差分（upwind differencing），其为一阶精度。

此格式是有界的（无振荡），但存在数值扩散。

3.3 二阶迎风格式

如下图所示意，对流通量值可计算为：

这种类型的插值方案被称为二阶迎风差分(second order upwind differencing，SOU)、线性迎风差分(linear upwind differencing, LUD)或Beam-Warming，该插值格式具有二阶精度。对于强对流或流动存在强梯度情况时，此格式存在振荡（无界格式）。

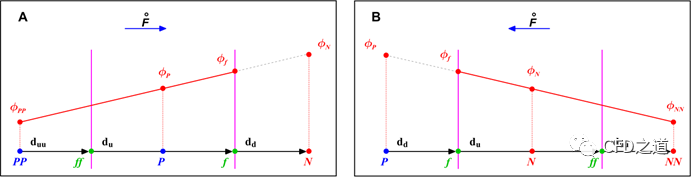
为防止SOU格式的求解振荡，可以增加斜率限制器函数：

当限制器检测到强梯度或强斜率变化时，其会在局部切换到低分辨率格式(一阶迎风格式)。

限制器函数的概念基于连续梯度的比率监测，例如，

通过增加一个精心设计的限制器，可以得到高分辨率格式（二阶精度）和有界格式（HR），这是一个TVD格式。

3.4 TVD格式

在CFD中，我们需要一个稳定的、无振荡的、有界的、高阶精度计算格式。Sweby图给出的下图描述了TVD的充要条件。图中阴影区域表示可采用的TVD区域。然而并非所有的限制器函数都是二阶精度的。图中高分辨率格式落在蓝色区域，低分辨率格式落在灰色区域。限制器的缺点是当r<0时，它们会局部地将格式精度降低到一阶(低分辨率格式)。然而当它能起到抑制振荡的作用时，这是合理的。

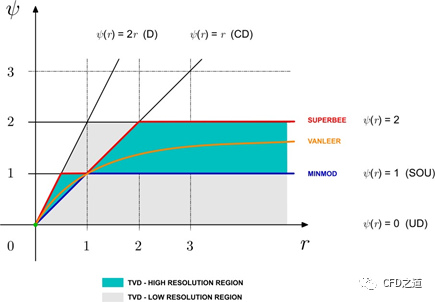
图中的UD = upwind；SOU = second order upwind；CD = central differencing；D = downwind。目前还没有一个特定的限制器可以很好地解决所有的问题，而特定的选择通常是在反复试验的基础上做出的。

下面比较upwind、 linear upwind、linear、Minmod TVD格式在数值格式杀手级测试案例（均匀矢量场(纯对流)中的双倾斜双台阶分布）中的表现，即使这个问题看起来很容易，但从数值上看，由于强烈的不连续性导致问题很难求解。要计算的问题如下所示。

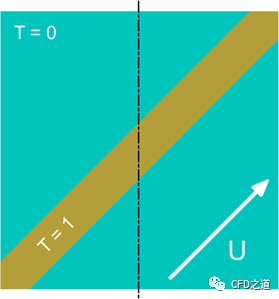
此问题有精确解（图中黑色线条上的温度分布）：

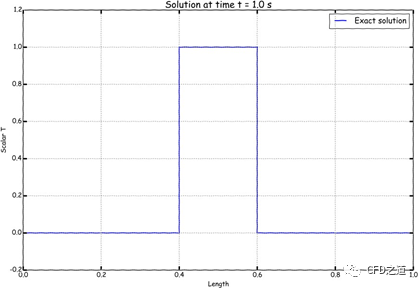
采用不同的求解格式得到的温度分布如下图所示。

定量比较如下图所示。

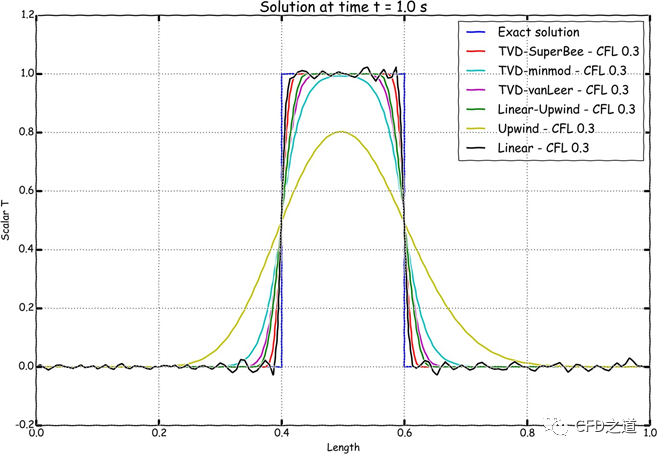
3.5 非结构网格插值处理

前面关于网格面上通量值的计算中，假设了一个线性结构（单元中心是对齐的），如下图A所示。

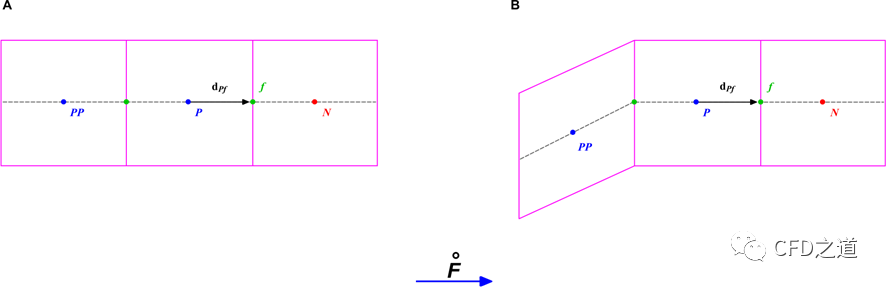
在非结构化网格中(通常用于工业情况)，多数情况下单元格中心PP与连接单元格P和N的向量不对齐(上图B)，因此前面的计算公式想要推广到非结构网格中并不太容易。

绕过此问题的一种简单方式是根据控制体P处的梯度重新定义高阶格式。例如，对于下图所示的网格系统，

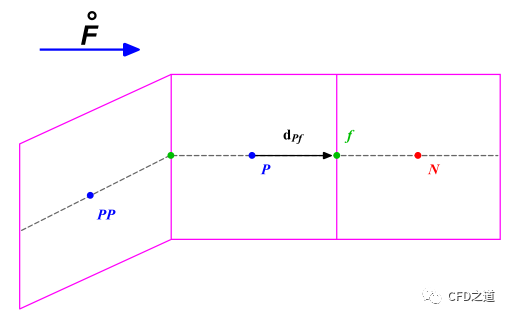
使用网格梯度值可以采用如下方式计算面值，

注意到在新格式中，网格并未出现。现在问题转向计算网格中心和面中心的梯度值上。例如可以使用高斯方法计算网格中心的梯度，然后插值到面中心。

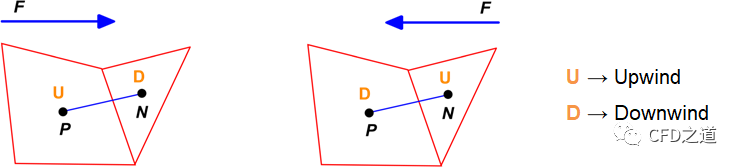
在非结构化网格中，由于节点PP的值通常不可用或无法直接计算，因此可采用下面的方式计算相邻梯度的比率，

可以看出，的值取决于流动方向。

3.6 网格中心梯度计算

目前有非常多的用于计算网格中心梯度的方法，如least squares、Gauss cell-based、Gauss node-based等。

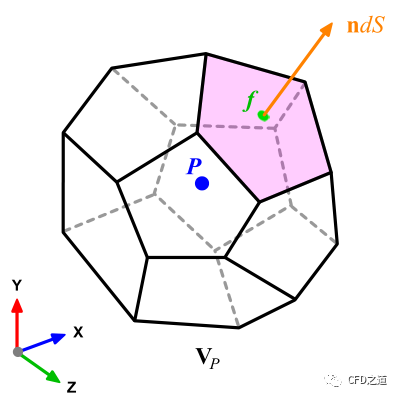
使用Gauss cell-based方法，网格体中心梯度可采用下面的方式计算：

如果网格质量可以接受，此计算方法具有二阶精度。通常最小二乘法要更加精确。

3.6 面梯度计算

面梯度（）产生于对流项与扩散项的离散过程。一种面梯度计算方式是使用网格中心梯度与的加权插值，采用此种方法，网格非正交性及偏斜都会对梯度计算产生误差，通常需要修正。修正过程是一个迭代的过程，在此过程中，通常先给定一个初始值，然后不断迭代得到一个更好的梯度近似值。

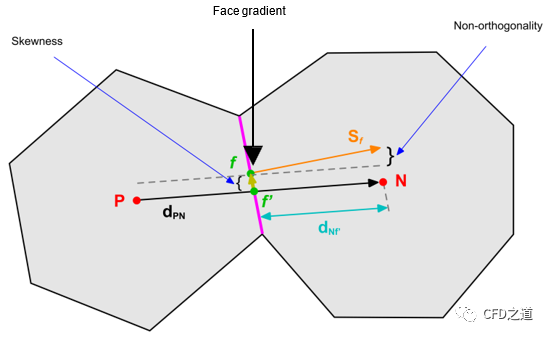
在下图所示的正交网格中，扩散通量中出现的界面梯度值可以采用下面的方式进行计算：

这里采用的是中心差分格式，具有二阶计算精度。

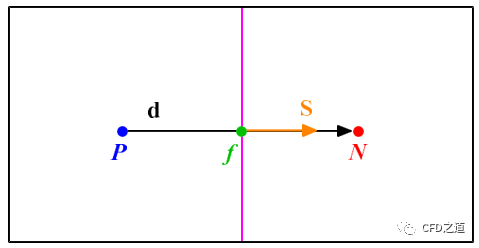
而在下图所示的非正交网格内，界面梯度值计算为：

该计算方法具有二阶精度，但包含较大的截断误差。

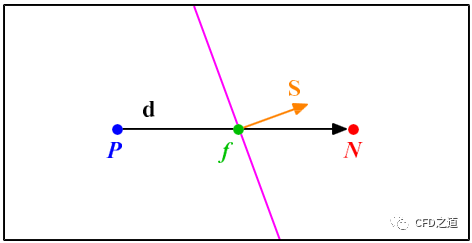
对于如下图所示的非正交网格系统：

这里采用的是超松弛的方法。

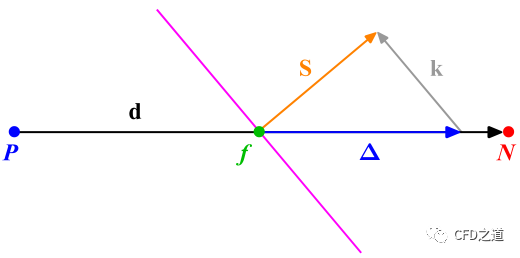
为了保证二阶计算计算精度，在应用中需要校正网格面的非正交及偏斜。当然理想情况下是生成具有正交性且无偏斜的网格，但实际应用中很难做到。注意这里的正交指的是网格面网格体心向量方向一致，偏斜指的是体心向量与网格面的相交位置与网格面心位置不重合（如下图中的）。

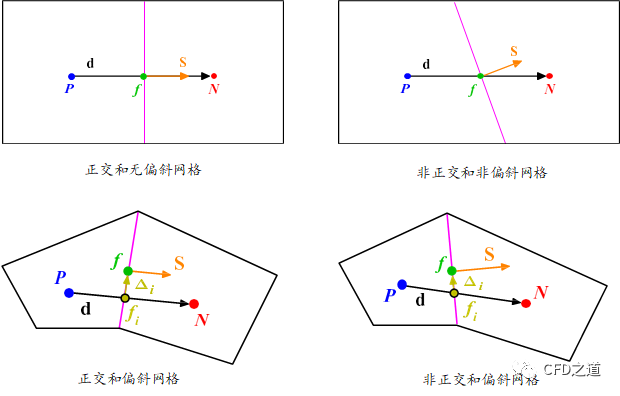
注：在实际应用过程中，尽可能的提高网格正交性，降低网格歪斜度。

”

4 时间离散

将控制方程对时间积分，可离散成下面的形式：

对于时间离散，可以使用的离散格式包括：Crank-Nicolson、Euler implicit、forward euler、backward differencing、adams-bashforth及adams-moulton等。

在进行时间离散时，瞬态项的离散方式可以与空间项不同，可以对每一项采用不同的离散方法，只要保证每一项离散至少为二阶，则整体离散方程的精度为二阶。

5 线性方程组求解

经过空间与时间离散后，可以将代数方程组装成线性方程组：

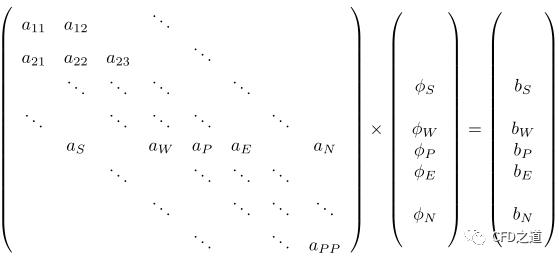
代数工程组可以使用迭代法或直接法进行求解。

6 OpenFOAM中的离散

OpenFOAM中整个计算区域内将任意多面体控制体中的控制方程在空间和时间上进行离散。用这种方法组装线性代数方程组，之后求解代数方程组得到输运物理量的解。因此，需要向OpenFOAM®提供以下信息：

• 计算区域离散。区域离散后的网格信息保存在文件夹constant/polyMesh中
• 边界条件与初始条件。信息保存在0文件夹中
• 物理属性。如密度、粘度、扩散系数、重力加速度等，保存在constant文件夹中
• 物理模型。如湍流模型、传质传热、多相流、燃烧等，保存在constant和/或system文件夹中
• 控制方程空间离散。包括扩散项、对流项、梯度项以及源项，参数保存在system/fvSchemes文件中
• 时间项离散。参数保存在system/fvSchemes文件中
• 代数方程求解。参数保存在system/fvSolution文件中
• 求解器运行控制。参数保存在system/controlDict文件中

6.1 fvSchemes文件

fvSchemes文件中可以指定出现在控制方程中的不同项的离散格式。一个简单的fvSchemes文件如下所示：

// 指定瞬态项离散格式
ddtSchemes
{
    default backward;
}
// 指定梯度项离散格式
gradSchemes
{
    default  Gauss linear;
    grad(p)         Gauss linear;
}
// 指定对流项离散格式
divSchemes
{
    default  none;
    div(phi,U)      Gauss linear;
}
// 指定扩散项离散格式
laplacianSchemes
{
    default Gauss linear orthogonal;
}
// 指定网格面插值格式
interpolationSchemes
{
    default linear;
}
// 指定面法向梯度插值格式
snGradSchemes
{
    default orthogonal;
}

fvScheme文件中指定的控制项包括：

1、ddtSchemes项

ddtSchemes：指定的是瞬态项的离散格式，源代码位于$WM_PROJECT_DIR/src/finiteVolume/finiteVolume/ddtSchemes中，常用的算法包括：

• steadyState：稳态模拟（显式/隐式）
• Euler：一阶格式（显式/隐式），有界
• backward：二阶格式（隐式），有界/无界
• CrankNicolson：二阶格式（隐式），有界/无界

一阶方法有界并且稳定，但具有数值扩散性。二阶方法是准确的，但它们在求解计算过程中可能会振荡。如果在使用欧拉法时将CFL保持在1以下，则数值扩散不会太大。OpenFOAM中实现的Crank-Nicolson方法使用了混合因子：

ddtSchemes
{
    default CrankNicolson Ψ;
}

参数等同于Euler方法（比较稳健但只有一阶精度）；为Crank-Nicolson方法（具有二阶精度，但是存在振荡）；如果将混合因子设置为0.5，则可以得到介于一阶精度和二阶精度之间的值。对于大多数应用，0.7-0.9的混合系数是比较合适的（稳定且准确）。

2、gradSchemes项

gradSchemes指定的是梯度项的离散格式。代码源代码位于$FOAM_SRC/finiteVolume/finiteVolume/gradSchemes。OpenFOAM主要提供了三种梯度项离散方法：

• Gauss linear：基于单元的高斯方法
• Gauss pointLinear：基于节点的高斯方法，通常比基于单元的高斯方法精度要高
• leastSquares：最小二乘法，大多数问题建议选择此方法

为了避免梯度计算过度或不足，通常使用梯度限制器以提高方法的稳健性，但同时也增加了数值扩散。梯度限制器源码位于路径$FOAM_SRC/finiteVolume/finiteVolume/gradSchemes/limitedGradSchemes中，OpenFOAM中主要提供了以下几种限制器：cellLimited, cellMDLimited, faceLimited, faceMDLimited等。所有的梯度离散算法至少都是二阶精度。

cell限制器将限制网格到网格的值，face限制器将限制网格面对网格值。多向（维）限制器（cellMDLimited和faceMDLimited）将对单独作用在每一个面方向上。标准限制器（cellLimited和faceLimited）将限制器应用于所有的梯度分量。

OpenFOAM中实现的梯度限制器可以使用混合因子，如下面的示例：

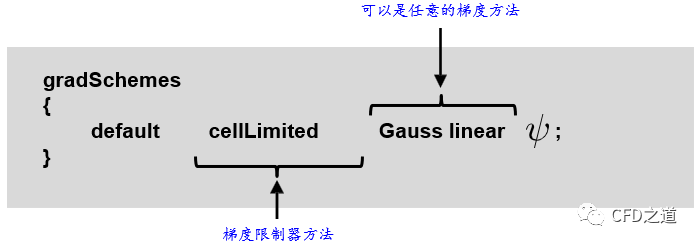
设置 参数将关闭限制器，此时可以获取最精确的计算结果，但可能求解振荡；设置参数可以获取最稳健的计算过程，但是会损失计算精度。通常可以设置得到一个折中的方案。

3、divSchemes项

divschemes指定的是对流项的离散格式。

代码位于$FOAM_SRC/finiteVolume/interpolation/surfaceInterpolation，OpenFOAM中提供了一些常用的对流项离散算法：

• upwind：一阶精度，迎风格式
• linearUpwind：二阶精度，有界格式
• linear：二阶精度，无界格式
• vanLeer或Minmod：TVD格式，二阶精度，有界格式
• limitedLinear：二阶精度，无界格式，但稳定性要比linear要好，通常建议用于LES模拟中
• LUST：混合格式，75%的linear+25%的linearUpwind格式

一阶方法是有界的，稳定的，但存在数值扩散，二阶方法精度高，但求解过程可能会振荡。

在为对流项div(phi,U)指定为linearUpwind格式时，需要事先指定grad(U)的离散格式。

gradSchemes
{
    grad(U) cellMDLimited Gauss linear 1.0;
}
divSchemes
{
    div(phi,U)  Gauss linearUpwind  grad(U);
}

4、snGradSchemes项

snGradSchemes项离散指的是网格面修正项的离散，源代码位于$FOAM_SRC/finiteVolume/finiteVolume/snGradSchemes路径下。OpenFOAM中提供了以下一些算法：

• orthogonal：主要用于无网格尺寸变化的六面体网格（理想网格），二阶精度，无需非正交校正。此方法中：

• corrected：用于具有网格尺寸渐变和非正交的网格。有非正交校正功能，具有二阶精度（取决于网格的质量），有界。

• limited：用于具有网格尺寸渐变和非正交的网格。二阶精度（取决于网格的质量），并具有非正交校正能力
• uncorrected：通常限于非正交性非常低的六面体网格。二阶精度，无非正交校正。稳定性好但比limited和corrected方法具有更强的数值扩散

6.2 方法选择

1. 下面的方法组合适合于大多数的算例。

• 该设置等效于大多数商业求解器中找到的默认方法
• 此设置具有二阶精度的并且完全有界
• 根据网格的质量，可能需要选项laplacianSchemes和snGradSchemes关键字的混合因子。
• 为了使时间扩散最小，建议使用小于2的CFL值，最好是小于1的CFL值。
• 如果在仿真过程中湍流量变得无界，则可以安全地将离散化方案更改为迎风
• 对于梯度离散，minimumSquares方法更准确。但是该方法在四面体网格中有些振荡

ddtSchemes
{
    default CrankNicolson 0;
}
gradSchemes
{
    default cellLimited Gauss linear 0.5;
    grad(U) cellLimited Gauss linear 1;
}
divSchemes
{
    default  none;
    div(phi,U)       Gauss linearUpwindV grad(U);
    div(phi,omega)  Gauss linearUpwind default;
    div(phi,k) Gauss linearUpwind default;
    div((nuEff*dev(T(grad(U)))))  Gauss linear;
}
laplacianSchemes
{
    default Gauss linear limited 1;
}
interpolationSchemes   
{
    default linear;
}
snGradSchemes
{
    default limited 1;
}

2. 下面的方法具有最高的精度，但求解可能存在振荡。

• 如果希望获得更高的精度，则可以使用此方法。
• 总体而言，此设置具有二阶精度，但具有振荡
• 通常将此设置用于LES模拟或层流，计算区域中没有复杂的物理场和网格
• 对高质量的网格使用此方法
• 根据网格的质量，需要更改laplacianSchemes和snGradSchemes关键字的混合因子

ddtSchemes
{
    default backward;
}
gradSchemes
{
    default Gauss leastSquares;
}
divSchemes
{
    default  none;
    div(phi,U)       Gauss linear;
    div(phi,omega)  Gauss limitedlinear 1;
    div(phi,k) Gauss limitedLinear 1;
    div((nuEff*dev(T(grad(U)))))  Gauss linear;
}
laplacianSchemes
{
    default Gauss linear limited 1;
}
interpolationSchemes
{
    default linear;
}
snGradSchemes
{
    default limited 1;
}

3. 下面的方法具有最好的稳定性，但也具有最大的数值扩散

• 此设置方案计算非常稳定，但数值扩散较为严重
• 此设置在时间和空间上都是一阶的。
• 可以使用此设置在存在劣质网格或强不连续性的情况下启动求解
• 可以开始使用一阶方法，然后切换到二阶方法
• 根据网格的质量，需要更改laplacianSchemes和snGradSchemes关键字的混合因子
• 可以使用此方法进行调试计算

ddtSchemes
{
    default Euler;
}
gradSchemes
{
    default cellLimited Gauss linear 1;
    grad(U) cellLimited Gauss linear 1;
}
divSchemes
{
    default  none;
    div(phi,U)       Gauss upwind;
    div(phi,omega)  Gauss upwind;
    div(phi,k) Gauss upwind;
    div((nuEff*dev(T(grad(U)))))  Gauss linear;
}
laplacianSchemes
{
    default Gauss linear limited 0.5;
}
interpolationSchemes
{
    default linear;
}
snGradSchemes
{
    default limited 0.5;
}