初始值通常是针对于过程变量来讲的,对于状态变量提初始值是没有实际意义的。就好比说你美餐了一顿之后,感觉内存有货状态满满,这时候去关注你是从饥肠辘辘开始吃的还是从半饱开始吃,多半是没有太大意义的。
瞬态计算考虑的是过程,计算结果得到的是过程变量,因此初始值至关重要。就比如说,给你3分钟吃饭时候,如果你从饥肠辘辘的状态开始,3分钟结束后你可能还没有吃饱,那如果从半饱开始吃,那3分钟结束后可能已经吃饱了。而且在这3分钟时间内,每一刻的状态都不一样。在瞬态计算中,初始值直接影响到后续的发展过程,直接决定了后续每一个时刻的状态,因此要好生对待。当然瞬态计算的初始值也容易确定,真实世界中起始时刻模型的状态就是初始值,不需要改也不能改。
然而稳态计算得到的是状态值,求取的是状态变量,得到的是系统平衡状态下的物理量分布。就好比吃饭,给10分钟吃饱了,20分钟还是吃饱了,一个小时还是吃饱,状态并不会有多大的改变,江湖俗称达到收敛。照这么说,起始状态应该不影响到最终状态才对,不管是完全饥饿状态开工还是从半饱状态开工,只要时间充足,最终状态都应该是吃饱了才对。的确是这样,起始状态虽然不会影响到最终状态,但会影响吃饱所需的时间。从完全饥饿状态到吃饱所需的时间肯定要比半饱状态开工所需的时间更多。
额,有点偏离主题了。今天要说的是为何稳态求解也需要用到初始值。事情还得从CFD计算过程说起。
地球人都知道,所谓的CFD计算,实际上是将描述物理现象的偏微分方程转化为代数方程组,然后利用计算机求解代数方程组,从而获取每一个物理量值的分布。整个过程中,代数方程组的求解极其的消耗计算机资源。先来看看代数方程组求解。
1 代数方程组的求解
例如要求解如下的代数方程组:
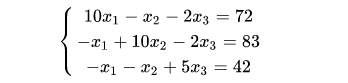
这是个三元一次方程组,中学生也都能求解,最常见的求解方式无异于采用消去法。当然我们在数值分析课上还学过很多其他的方法,除了消去法外,还有什么克拉默法、三角分解法等等。
利用消去法求解上面的代数方程组,python代码可写成:
import matplotlib.pyplot as plt
from pylab import mpl
import math
def calculate_parameter(data):
# i用来控制列元素,line是一行元素,j用来控制循环次数,datas用来存储局部变量。保存修改后的值
i = 0
j = 0
line_size = len(data)
# 将行列式变换为上三角行列式
while j < line_size - 1:
line = data[j]
temp = line[j]
templete = []
for x in line:
x = x / temp
templete.append(x)
data[j] = templete
# flag标志应该进行消元的行数
flag = j + 1
while flag < line_size:
templete1 = []
temp1 = data[flag][j]
i = 0
for x1 in data[flag]:
if x1 != 0:
x1 = x1 - (temp1 * templete[i])
templete1.append(x1)
else:
templete1.append(0)
i += 1
data[flag] = templete1
flag += 1
j += 1
# 求相应的参数值
parameters = []
i = line_size - 1
# j标识减去元素个数
# flag_rol标识除那一列
flag_j = 0
rol_size = len(data[0])
flag_rol = rol_size - 2
# 获得解的个数
while i >= 0:
operate_line = data[i]
if i == line_size - 1:
parameter = operate_line[rol_size - 1] / operate_line[flag_rol]
parameters.append(parameter)
else:
flag_j = (rol_size - flag_rol - 2)
temp2 = operate_line[rol_size - 1]
# result_flag为访问已求出解的标志
result_flag = 0
while flag_j > 0:
temp2 -= operate_line[flag_rol +
flag_j] * parameters[result_flag]
result_flag += 1
flag_j -= 1
parameter = temp2 / operate_line[flag_rol]
parameters.append(parameter)
flag_rol -= 1
i -= 1
return parameters
paremeters = [[10, -1, -2, 72],
[-1, 10, -2, 83],
[-1, -1, 5, 42]]
results = calculate_parameter(paremeters)
print(" x1="+str(results[2])+"n x2="+str(results[1])+"n x3="+str(results[0]))运行后程序输出:
x1=11.0
x2=12.0
x3=13.000000000000002消去法的思路简单且逻辑清晰,但是存在很大的问题。分析上面的程序可以看到,要利用消去法求解方程组,需要创建系数矩阵。对于上面方程组需创建矩阵为:
paremeters = [[10, -1, -2, 72],
[-1, 10, -2, 83],
[-1, -1, 5, 42]]上面的方程组很简单,系数矩阵不过3x4。然而在流体仿真计算中,网格数量动辄成百上千万,将如此庞大的矩阵存入内存,则需要巨大容量的内存。
粗略估计,假如计算网格有一百万网格,则形成的方程组的方程数量有100万个,每个方程包含100万个未知数,这样需要创建100万x100万的矩阵来存储系数,至少需要1000G的内存才能够放得下。(这里是不严谨的初步估计)。
注:上面的估计是最坏的估计,事实上CFD代数方程组中很多的系数为0,是典型的稀疏矩阵,采用特殊设计的数据结构,可以缓解内存消耗。
事实上100万网格数量并不多,工程中动不动就几百万几千万的网格数量,如果采用直接求解,内存小了根本玩不动,因此人们采用迭代法来求解这种大规模的矩阵。
迭代法计算最大的好处是不需要将所有的系数总装成一个大矩阵存入内存,但是也带来了求解精度和计算收敛方面的问题。
受计算机内存限制,大规模线性方程组常采用迭代法进行求解。
2 迭代法求解方程组
还是上面的的线性方程组:
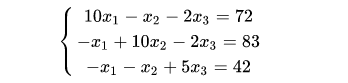
采用迭代法进行求解。迭代法求解线性方程组最简单的莫过于jacobi迭代。
先将上面的方程组改写成下面的形式:
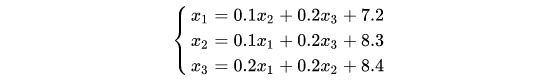
在利用jacobi迭代法改写成迭代式:
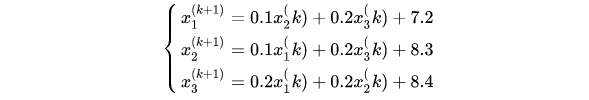
可以采用程序求解:
def f(x1,x2,x3,count=1):
y1=0.1*x2+0.2*x3+7.2
y2=0.1*x1+0.2*x3+8.3
y3=0.2*x1+0.2*x2+8.4
if abs(y1-x1)<0.0001 and abs(y2-x2)<0.0001 and abs(y3-x3)<0.0001:
#设定精度为0.0001
print('最终的计算结果为%s、%s和%s' %(y1,y2,y3))
else:
print('第%s次迭代的计算结果为%s、%s和%s' %(count, y1,y2,y3))
x1,x2,x3,count=y1,y2,y3,count+1
return f(x1,x2,x3,count)
f(3,5,5)
#设置初始值为(3,5,5)注:迭代法并不需要将方程组所有系数一起读入内存。求解过程中是采用顺序求解,一次只计算一个代数方程,100万个方程组成的方程组,一次完整迭代需要计算100万次。这里的一次完整迭代对应于流体计算中的一个迭代步。所以当网格数量很多时,计算一步也需要很长的时间。
这里设置初始值(3,5,5),计算输出为:
第1次迭代的计算结果为8.7、9.600000000000001和10.0
第2次迭代的计算结果为10.16、11.170000000000002和12.06
第3次迭代的计算结果为10.729000000000001、11.728000000000002和12.666
第4次迭代的计算结果为10.906、11.906100000000002和12.8914
第5次迭代的计算结果为10.968890000000002、11.968880000000002和12.962420000000002
第6次迭代的计算结果为10.989372000000001、11.989373和12.987554000000001
第7次迭代的计算结果为10.9964481、11.996448000000001和12.995749
第8次迭代的计算结果为10.9987946、11.998794610000001和12.99857922
第9次迭代的计算结果为10.999595305、11.999595304000001和12.999517842000001
第10次迭代的计算结果为10.9998630988、11.9998630989和12.9998381218
第11次迭代的计算结果为10.999953934250001、11.99995393424和12.99994523954
最终的计算结果为10.999984441332、11.999984441333002和12.999981573698001可以看出一共迭代了11次,计算收敛,得到解为(11,12,13)。
尝试采用比较接近最终解的初始值,如调用f(10,11,12),可得到输出:
第1次迭代的计算结果为10.700000000000001、11.700000000000001和12.600000000000001
第2次迭代的计算结果为10.89、11.89和12.88
第3次迭代的计算结果为10.965、11.965000000000002和12.956000000000001
第4次迭代的计算结果为10.9877、11.9877和12.986
第5次迭代的计算结果为10.99597、11.995970000000002和12.995080000000002
第6次迭代的计算结果为10.998613、11.998613000000002和12.998388
第7次迭代的计算结果为10.999538900000001、11.999538900000001和12.9994452
第8次迭代的计算结果为10.99984293、11.999842930000002和12.999815560000002
第9次迭代的计算结果为10.999947405、11.999947405和12.999937172000001
最终的计算结果为10.999982174900001、11.999982174900001和12.999978962迭代9次得到最终解。有兴趣的小伙伴也可以尝试其他偏离最终解的初始值代入计算,看看收敛性如何。
随着变量的增加,更难找到合适的初始值。
还有一个问题,这里有3个未知数,因此初始值需要提供3个值,那如果其中某一个值严重偏离目标值,计算结果会怎样呢?利用赛德尔迭代,采用初始值(10,11,120),输出为:
第1次迭代的计算结果为32.300000000000004、33.3和12.600000000000001
第2次迭代的计算结果为13.05、14.05和21.520000000000003
第3次迭代的计算结果为12.909000000000002、13.909000000000002和13.82
第4次迭代的计算结果为11.3549、12.3549和13.763600000000002
第5次迭代的计算结果为11.188210000000002、12.188210000000002和13.141960000000001
第6次迭代的计算结果为11.047213000000001、12.047213000000001和13.075284000000002
第7次迭代的计算结果为11.0197781、12.019778100000002和13.018885200000001
第8次迭代的计算结果为11.00575485、12.005754850000002和13.00791124
第9次迭代的计算结果为11.002157733、12.002157733和13.00230194
第10次迭代的计算结果为11.0006761613、12.000676161300001和13.000863093200001
第11次迭代的计算结果为11.00024023477、12.00024023477和13.00027046452
第12次迭代的计算结果为11.000078116381001、12.000078116381001和13.000096093908
最终的计算结果为11.000027030419702、12.000027030419702和13.000031246552401可以看到,共迭代了12次才收敛到最终结果,随着初始值的偏离,计算迭代次数也会随之增多。
当然这里只有3个未知数,对于流体计算网格非常多的时候,未知数的数量也会随之增多,想要提供一个良好的初始值也就非常困难了。
注:上述代码参考自https://zhuanlan.zhihu.com/p/25548025
3 Fluent中的初始值
Fluent提供了3种初始化的方式:
-
Hybrid Initialization
-
Standard Initialization
-
FMG初始化
通过双击模型树节点Initialization,可在右侧面板中选择初始化方式。

FMG初始化需要采用TUI命令激活。
3.1 Standard Initialization
这是传统的初始化方式。选择该选项后,会弹出初始值设置面板,如下图所示。
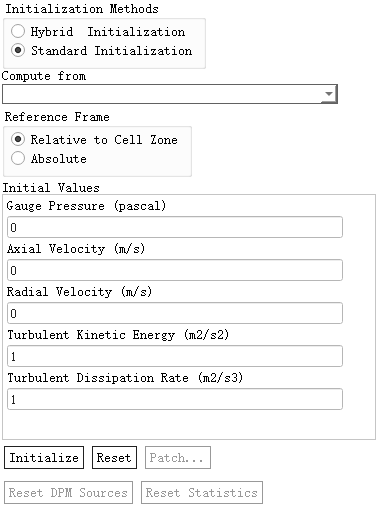
Fluent会根据用户选择的模型动态调整所需要的初始化值。用户可以通过选择该面板中下拉框Compute from来辅助填写初始值。
采用Standard Initialization初始化,实现的是给整体区域赋均匀的初始值,若有特殊要求,可以利用Patch进行补充,也可以采用UDF宏DEFINE_INIT进行特别定义。
对于下面的模型,入口速度10m/s,其他边界皆为壁面。
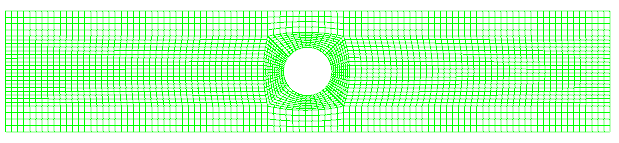
如下图所示采用标准初始化,指定区域的速度与湍流条件。
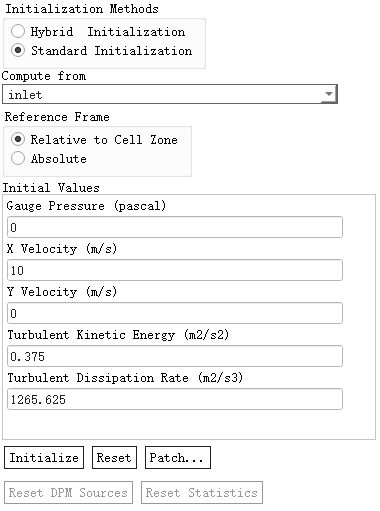
初始化完毕后区域内速度场分布如下图所示。
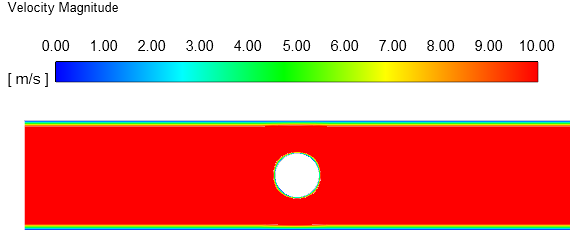
可以看出,除了壁面附近,其他区域均采用的是均匀速度分布。
3.2 Hybrid初始化
改用Hybrid初始化。

此时初始速度场分布如下图所示。
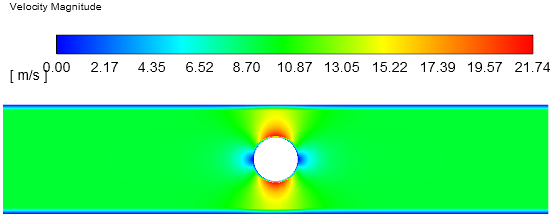
与上面的相比,采用hybrid方式进行初始化得到的初始流场分布似乎更贴近真实稳态流场分布。
3.3 FMG初始化
FMG初始化需要使用TUI命令激活,且需要先进行标准初始化或Hybrid初始化。
激活命令为:
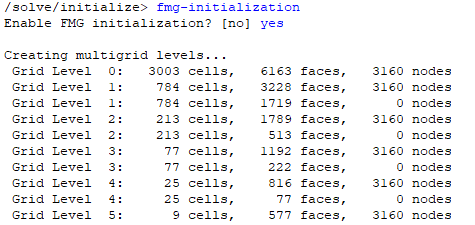
/solve/initialize/fmg-initialization
如下图所示采用FMG初始化。
初始化完毕后流场分布如下图所示。
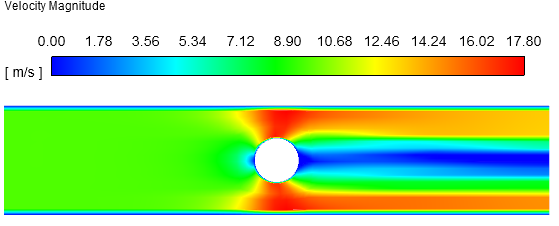
谁更贴近最终情况?一看便知。
注:当计算域有明确的进口与出口时,强烈建议采用FMG初始化,其次采用hybrid初始化。FMG初始化不能用于瞬态计算,瞬态计算时,常常先进行稳态计算,采用FMG做初始化得到稳态解后切换到瞬态求解。而hybrid及标准初始化可以用于瞬态和稳态计算。
关于Hybrid初始化以及FMG初始化的原理,可参阅软件理论文档21.8~21.9节,或等待后续文章。本文结束。
注:本文部分内容节选自《小白的CFD之旅》,转载请注明出处!


本篇文章来源于微信公众号: CFD之道








评论前必须登录!
注册