本文简单介绍求解线性方程组中的松弛迭代法以及松弛因子。
1 迭代法求解方程组
考虑线性方程组:
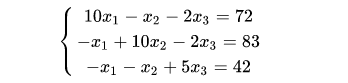
采用迭代法进行求解。
1.1 Jacobi迭代
迭代法求解线性方程组最简单的莫过于jacobi迭代。
在利用jacobi迭代法改写成迭代式:
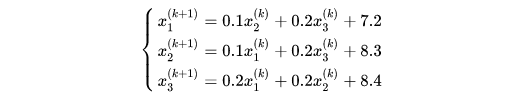
可以采用程序求解:
def f(x1,x2,x3,count=1):
y1=0.1*x2+0.2*x3+7.2
y2=0.1*x1+0.2*x3+8.3
y3=0.2*x1+0.2*x2+8.4
if abs(y1-x1)<0.0001 and abs(y2-x2)<0.0001 and abs(y3-x3)<0.0001:
#设定精度为0.0001
print('最终的计算结果为%s、%s和%s' %(y1,y2,y3))
else:
print('第%s次迭代的计算结果为%s、%s和%s' %(count, y1,y2,y3))
x1,x2,x3,count=y1,y2,y3,count+1
return f(x1,x2,x3,count)
f(3,5,5)
#设置初始值为(3,5,5)这里设置初始值(3,5,5),计算输出为:
第1次迭代的计算结果为8.7、9.600000000000001和10.0
第2次迭代的计算结果为10.16、11.170000000000002和12.06
第3次迭代的计算结果为10.729000000000001、11.728000000000002和12.666
第4次迭代的计算结果为10.906、11.906100000000002和12.8914
第5次迭代的计算结果为10.968890000000002、11.968880000000002和12.962420000000002
第6次迭代的计算结果为10.989372000000001、11.989373和12.987554000000001
第7次迭代的计算结果为10.9964481、11.996448000000001和12.995749
第8次迭代的计算结果为10.9987946、11.998794610000001和12.99857922
第9次迭代的计算结果为10.999595305、11.999595304000001和12.999517842000001
第10次迭代的计算结果为10.9998630988、11.9998630989和12.9998381218
第11次迭代的计算结果为10.999953934250001、11.99995393424和12.99994523954
最终的计算结果为10.999984441332、11.999984441333002和12.999981573698001可以看出一共迭代了11次,计算收敛,得到解为(11,12,13)。
1.2 Gauss-seidel迭代
在Jacobi迭代中,后面的迭代并没有应用到前面的结果。Gauss-Seidel迭代与之不同,后面的迭代利用到了前面的计算结果,如下所示,将前面的方程组改写成迭代式:
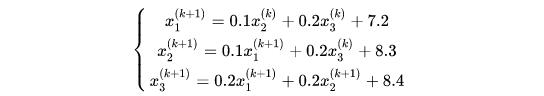
程序代码可写成:
#seidel 迭代法求根
def f(x1,x2,x3,count):
y1=0.1*x2+0.2*x3+7.2
y2=0.1*y1+0.2*x3+8.3
y3=0.2*y1+0.2*y2+8.4
if max(abs(y1-x1), abs(y2-x2), abs(y3-x3))<0.0001:
#设定精度为0.0001
print('最终的计算结果为%s、%s和%s' %(y1,y2,y3))
else:
print('第%s次迭代的计算结果为%s、%s和%s' %(count, y1,y2,y3))
x1,x2,x3,count=y1,y2,y3,count+1
return f(x1,x2,x3,count)
f(3,5,5,1)
#设置初始根为(3,5,5)输出结果为:
第1次迭代的计算结果为8.7、10.170000000000002和12.174
第2次迭代的计算结果为10.651800000000001、11.799980000000001和12.890356
第3次迭代的计算结果为10.9580692、11.973878120000002和12.986389464000002
第4次迭代的计算结果为10.994665704800001、11.996744463280002和12.998282033616
第5次迭代的计算结果为10.999330853051202、11.99958949202832和12.999784069015906
第6次迭代的计算结果为10.999915763006014、11.999948390103784和12.99997283062196
最终的计算结果为10.999989405134771、11.999993506637871和12.9999965823545281.3 松弛迭代
松弛迭代可以看成是高斯-赛德尔迭代的改进。改造迭代形式为:
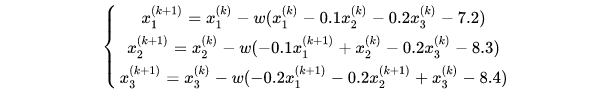
注:从松弛迭代形式可以看出,收敛的计算结果是不依赖于松弛因子w的取值的。
对应的程序代码:
#sor迭代法
# -*- coding: utf-8 -*-#
def f(x1, x2, x3, w, count=1):
y1 = x1-w*(x1-0.1*x2-0.2*x3-7.2)
y2 = x2-w*(-0.1*y1+x2-0.2*x3-8.3)
y3 = x3-w*(-0.2*y1 -0.2 *y2+x3-8.4)
if max(abs(y1-x1), abs(y2-x2), abs(y3-x3)) < 0.0001:
# 设定精度为0.0001
print('最终的计算结果为%s、%s和%s' % (y1, y2, y3))
else:
print('第%s次迭代的计算结果为%s、%s和%s' % (count, y1, y2, y3))
x1, x2, x3, count = y1, y2, y3, count+1
return f(x1, x2, x3, w, count)
f(3,5,5,1) #设置松弛因子为1运行后输出:
第1次迭代的计算结果为8.7、10.170000000000002和12.174
第2次迭代的计算结果为10.651800000000001、11.799980000000001和12.890356
第3次迭代的计算结果为10.9580692、11.97387812和12.986389464
第4次迭代的计算结果为10.994665704800001、11.99674446328和12.998282033616
第5次迭代的计算结果为10.999330853051202、11.99958949202832和12.999784069015904
第6次迭代的计算结果为10.999915763006014、11.999948390103782和12.99997283062196
最终的计算结果为10.99998940513477、11.99999350663787和12.999996582354528可看到输出结果与赛德尔迭代完全相同。
注:松弛迭代法中,当松弛因子w=1时,即为高斯-赛德尔迭代;w>1时为超松弛迭代;w<1时为亚松弛迭代。
下面改变松弛因子看看有什么不同,验证结果如下表所示。
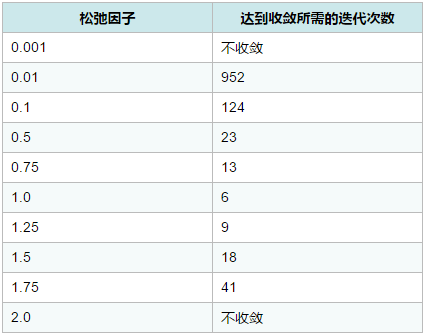
注:在这个方程组中,松弛因子为1时收敛性表现最好。但要注意并非所有情况下都是松弛因子为1时收敛性最好。关于松弛因子与收敛性间的关系,可参阅任何一本数值分析教材。
从表中可以看出,松弛因子并非越小越好,也并非越大越好,在实际计算过程中,需要根据收敛性来调整松弛因子的值。
2 Fluent中的松弛因子
Fluent中采用的是亚松弛迭代。所有松弛因子取值范围为0~1。
鼠标双击模型树节点Solution > Controls,即可在右侧面板中设置松弛因子。
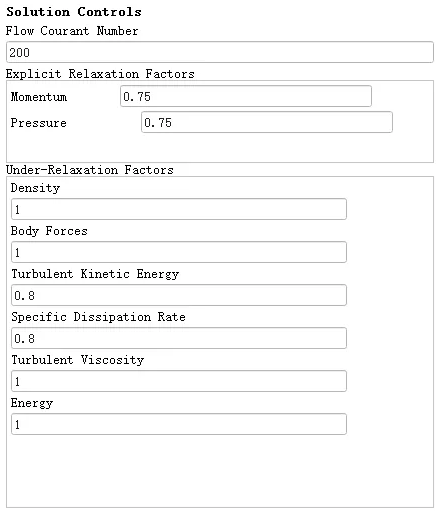
关于Fluent中的亚松弛因子:
取值范围0~1
取值越大,收敛越快,计算稳定性越差;取值越小,收敛越慢,稳定性更好
当残差震荡厉害时,可适当减小松弛因子;当残差曲线变化量很小且非常平缓时,可增大松弛因子
只要计算达到收敛,松弛因子不会影响计算结果

注:本文部分内容来自连载《小白学CFD》,转载请务必保持文章完整性!
本篇文章来源于微信公众号: CFD之道








评论前必须登录!
注册